
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь закона сохранения импульса с однородностью пространстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнения движения
Путь — длина участка траектории материальной точки, пройденного ею за определённое время. Перемещение в классической механике — направленный отрезок, характеризующий изменение положения материальной точки (тела) в пространстве. Обладает свойствами вектора, поэтому является векторной величиной. Обладает свойством аддитивности. Длина отрезка — это модуль перемещения, измеряется в метрах (СИ).Перемещением также называют процесс изменения положения. Скорость – это векторная физическая величина, введенная для определения быстроты движения и его направления в данный момент времени. Линейная скорость Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением
Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением
Здесь R - радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения
1.2 Кинема́тика твёрдого тела (от др.-греч. движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины. Движение тела может быть как поступательным так и вращательным. В этом случае тело представляется в виде системы жестко связанных между собой материальных точек. При поступательном движение любая прямая, проведенная в теле, перемещается параллельно самой себе. По форме траектории поступательное движение может быть прямолинейным и криволинейным. При поступательном движении все точки твердого тела за один и тот же промежуток времени совершают равные по величине и направлению перемещения Следовательно, скорости и ускорения всех точек тела в любой момент времени также одинаковы. Для описания поступательного движения достаточно определить движение одной точки. Вращательным движением твёрдого тела вокруг неподвижной оси называется такое движение, при котором все точки тела движутся _по окружностям, центры которых лежат на одной прямой (ось вращения). Ось вращения может проходить через тело или лежать за его пределами. Если ось вращения проходит сквозь тело, то точки, лежащие на оси, при вращении тела остаются в покое. Точки твёрдого тела, находящиеся на разных расстояниях от оси вращения за одинаковые промежутки времени проходят различные расстояния и следовательно имеют различные линейные скорости. угловая скорость - ω. По аналогии с линейной скоростью вводят понятия средней и мгновенной угловой скорости: Быстроту изменения угловой скорости характеризует среднее и мгновенное угловое ускорение. Вектор Угловое перемещение где В системе СИ угловое перемещение измеряется в радианах (рад.), угловая скорость угловое ускорение 1.3 Динамика материальной точки и поступательного движения твердого тела. Основная задача динамики материальной точки состоит в том, чтобы найти закон движения материальной точки, зная приложенные к ней силы, или наоборот, по известному закону движения определить силы, действующие на эту точку. Обратная задача динамики: по заданным силам определить характер движения тела. В проекциях на оси неподвижной прямоугольной декартовой системы координат уравнения основного закона динамики поступательного движения системы имеют вид: или 2. Простейшие случаи поступательного движения твердого тела. б) Движение под действием постоянной силы: где mv0 - количество движения тела в начальный момент времени t = 0.
Законы Ньютона 1-ый Инерциальными системами отсчета называются такие системы, в которых свободные (т.е. не участвующие во взаимодействиях с другими телами) тела движутся без ускорения (т.е. равномерно и прямолинейно) или покоятся (состояние покоя, вообще говоря, следует рассматривать как частный случай равномерного движения с нулевой скоростью). 2-ой скорость изменения импульса в материальной точке равна равнодействующей действующих всех сил на точку или в форме. 3-ий Внешние и внутренние силы Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом - Внутренние силы обладают следующими свойствами: 1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. по третьему закону динамики любые две точки системы действуют друг на друга с равными по модулю и противоположно направленными силами
2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю. если взять произвольный центр О, то
Из доказанных свойств не следует однако, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызывать взаимные перемещения этих точек или тел. Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно твердое тело. И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
Закон сохранения импульса: в замкнутой системе тел геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой. Закон сохранения импульса для упругого взаимодействия:
Закон сохранения импульса для неупругого взаимодействия:
где: m 1, m 2 - массы соударяющихся тел; v 1, v 2 - скорости тел до столкновения;
Однако для каждой из этих частиц Второй закон Ньютона
Центр масс системы геометрическая точка, характеризующая движение тела или системы частиц как целого.Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:
где
Раздел 3. Электродинамика Тема 3.1. Электростатика- раздел теории электричества, в котором изучается взаимодействие неподвижных электрических зарядов. Заряд и его свойства. Электрический заряд–это некая первичная характеристика материи, характеризующая способность объекта вступать в электромагнитное взаимодействие и создавать электромагнитное поле. Обозначается электрический заряд q и измеряется в СИ в кулонах (Кл). Электрический заряд–это свойство, присущее не телам, а частицам, из которых состоит вещество. Свойства электрического заряда: 1. Двузначность. Электрический заряд может быть положительным и отрицательным (принято считать, что протон заряжен положительно, а электрон – отрицательно). 2. Симметрия между положительным и отрицательным электричеством. Среди элементарных частиц одинаково часто встречаются заряды обоего знака. Положительные и отрицательные заряды способны компенсировать действие друг друга. Если в некотором теле одинаковое число частиц с зарядами того и другого знаков, то тело ведёт себя как электрически нейтральное. 3. Электрический заряд квантован, т.е. электрический заряд у тел может изменяться лишь дискретно, конечными порциями. Минимально возможная порция равна элементарному заряду. Элементарный электрический заряд (е = 1,6×10–19 Кл). В свободном состоянии все заряды кратны целому числу элементарных электрических зарядов: 4. Сохраняемость заряда выражается законом сохранения заряда: суммарный электрический заряд замкнутой системы сохраняется во всех процессах, происходящих с участием заряженных частиц: q1 + q2 +...+ qN= q1* + q2*+...+ qN*. 5. релятивистская инвариантность: величина полного заряда системы не зависит от движения носителей заряда (заряд движущейся и покоящейся частиц одинаков). Иными словами – во всех ИСО величина заряда любой частицы или тела одинакова. Это подтверждается тем, что атомы нейтральны при любой скорости движения электронов. Электрическое поле –это часть фундаментального электромагнитного поля, это особый вид материи, который существует вокруг заряженных тел или частиц. - это электрическое поле, не изменяющееся со временем. Оно создаётся неподвижными электрическими зарядами. Электрическое поле называется однородным, если во всех его точках векторы напряженности одинаковы, то есть совпадают по модулю и направлению. В противном случае поле неоднородно. Напряженность электростатического поля - физическая величина, определяемая силой, которая действует на пробный единичный положительный заряд, помещенный в эту точку поля:
Е0-электрическая постоянная (=8.85*10:-12 Ф/м) Принцип суперпозиции - напряжённость результирующего поля равна векторной сумме напряжённостей полей, создаваемых отдельными зарядами Поток вектора напряженности - Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности ФЕ через эту поверхность.
точечный заряд +q0 перемещается в поле неподвижного точечного заряда +q в вакууме из точки 1 в точку 2. Работа кулоновской силы, действующей на заряд Потенциал поля - потенциалом данной точки поля называется скалярная величина, численно равная величине потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд: φ=Wп/q.Потенциал данной точки поля численно равен работе сил электростатического поля по перемещению единичного положительного заряда из данной точки поля в бесконечность. Обозначается потенциал φ и в СИ измеряется в вольтах (В). Разность потенциалов φ1-φ2 между точками 1 и 2 численно равна работе, совершаемой силами поля при перемещении единичного положительного заряда по произвольному пути из точки 1 в точку 2. Связь напряженности и потенциала. Эти формулы выражают связь между напряжённостью и потенциалом только для однородного электрического поля. Циркуляция вектора напряженности электростатического поля. Интеграл Тема 3.2. Постоянный электрический ток. Электрический ток -упорядоченное движение заряженных частиц под действием сил электрического поля или сторонних сил. За направление тока выбрано направление движения положительно заряженных частиц. Электрический ток называют постоянным, если сила тока и его направление не меняются с течением времени. Электрический ток проводимости. Для получения электрического тока в проводнике помимо заряженных частиц (носителей электрического заряда) необходимо создать электрическое поле внутри проводника, т.е. разность потенциалов на концах проводника Сила и плотность тока. Сила тока равна величине заряда, проходящего в единицу времени через поперечное сечение проводника: Сила тока обозначается Плотность тока равна величине заряда, проходящего в единицу времени через единичную площадку, перпендикулярную линиям тока. Плотность тока обозначается Связь между силой тока Сопротивление проводников - некоторая способность материалов (точнее, веществ из которых и сделан сам проводник) противодействовать движению заряженных частиц внутри этого проводника. при этом противодействии происходит некоторое преобразование электрической энергии в иной её вид (в основном, электроэнергия преобразуется в тепло).Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как U — разность электрических потенциалов на концах проводника; I — сила тока, протекающего между концами проводника под действием разности потенциалов. Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он состоит. Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле: где ρ — удельное сопротивление вещества проводника, l — длина проводника, а S — площадь сечения. Разность потенциалов, ЭДС, напряжение. Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду. ЭДС - скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура. ЭДС можно выразить через напряжённость электрического поля сторонних сил ( ЭДС индукции Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением где Напряжение характеризует электрическое поле, создаваемое током. Напряжение (U) равно отношению работы электрического поля по перемещению заряда Закон Ома для однородного участка цепи - сила тока I в однородном металлическом проводнике прямо пропорциональна напряжению U на концах этого проводника и обратно пропорциональна сопротивлению R этого проводника: Закон Ома для неоднородного участка и замкнутой цепи Неоднородный участок цепи – это участок, содержащий ЭДС. Следовательно, для неоднородного участка цепи Работа и мощность постоянного тока. Работа тока - работа электрического поля по переносу электрических зарядов вдоль проводника. Работа электрических сил поля, или, что то же, работа электрического тока, может быть подсчитана по формуле
Так как q = It, то окончательно получим
где А — работа, дж; I — ток, а; t — время, сек; U —напряжение, в. По закону Ома, U= Ir. Поэтому формулу работы можно написать и так: Мощность- физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Р = IU. За единицу мощности ватт (Вт) принята мощность тока силой 1 А на участке с напряжением 1 В. Следовательно, 1 Вт = 1 А·1 В. Закон Джоуля-Ленца. Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля Математически может быть выражен в следующей форме:
Уравнения движения
Путь — длина участка траектории материальной точки, пройденного ею за определённое время. Перемещение в классической механике — направленный отрезок, характеризующий изменение положения материальной точки (тела) в пространстве. Обладает свойствами вектора, поэтому является векторной величиной. Обладает свойством аддитивности. Длина отрезка — это модуль перемещения, измеряется в метрах (СИ).Перемещением также называют процесс изменения положения. Скорость – это векторная физическая величина, введенная для определения быстроты движения и его направления в данный момент времени. Линейная скорость Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением
Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением
Здесь R - радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения
1.2 Кинема́тика твёрдого тела (от др.-греч. движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины. Движение тела может быть как поступательным так и вращательным. В этом случае тело представляется в виде системы жестко связанных между собой материальных точек. При поступательном движение любая прямая, проведенная в теле, перемещается параллельно самой себе. По форме траектории поступательное движение может быть прямолинейным и криволинейным. При поступательном движении все точки твердого тела за один и тот же промежуток времени совершают равные по величине и направлению перемещения Следовательно, скорости и ускорения всех точек тела в любой момент времени также одинаковы. Для описания поступательного движения достаточно определить движение одной точки. Вращательным движением твёрдого тела вокруг неподвижной оси называется такое движение, при котором все точки тела движутся _по окружностям, центры которых лежат на одной прямой (ось вращения). Ось вращения может проходить через тело или лежать за его пределами. Если ось вращения проходит сквозь тело, то точки, лежащие на оси, при вращении тела остаются в покое. Точки твёрдого тела, находящиеся на разных расстояниях от оси вращения за одинаковые промежутки времени проходят различные расстояния и следовательно имеют различные линейные скорости. угловая скорость - ω. По аналогии с линейной скоростью вводят понятия средней и мгновенной угловой скорости: Быстроту изменения угловой скорости характеризует среднее и мгновенное угловое ускорение. Вектор Угловое перемещение где В системе СИ угловое перемещение измеряется в радианах (рад.), угловая скорость угловое ускорение 1.3 Динамика материальной точки и поступательного движения твердого тела. Основная задача динамики материальной точки состоит в том, чтобы найти закон движения материальной точки, зная приложенные к ней силы, или наоборот, по известному закону движения определить силы, действующие на эту точку. Обратная задача динамики: по заданным силам определить характер движения тела. В проекциях на оси неподвижной прямоугольной декартовой системы координат уравнения основного закона динамики поступательного движения системы имеют вид: или 2. Простейшие случаи поступательного движения твердого тела. б) Движение под действием постоянной силы: где mv0 - количество движения тела в начальный момент времени t = 0.
Законы Ньютона 1-ый Инерциальными системами отсчета называются такие системы, в которых свободные (т.е. не участвующие во взаимодействиях с другими телами) тела движутся без ускорения (т.е. равномерно и прямолинейно) или покоятся (состояние покоя, вообще говоря, следует рассматривать как частный случай равномерного движения с нулевой скоростью). 2-ой скорость изменения импульса в материальной точке равна равнодействующей действующих всех сил на точку или в форме. 3-ий Внешние и внутренние силы Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом - Внутренние силы обладают следующими свойствами: 1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. по третьему закону динамики любые две точки системы действуют друг на друга с равными по модулю и противоположно направленными силами
2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю. если взять произвольный центр О, то
Из доказанных свойств не следует однако, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызывать взаимные перемещения этих точек или тел. Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно твердое тело. И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
Закон сохранения импульса: в замкнутой системе тел геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой. Закон сохранения импульса для упругого взаимодействия:
Закон сохранения импульса для неупругого взаимодействия:
где: m 1, m 2 - массы соударяющихся тел; v 1, v 2 - скорости тел до столкновения;
Однако для каждой из этих частиц Второй закон Ньютона
Связь закона сохранения импульса с однородностью пространства Однородность пространства, т. е. симметрия по отношению к преобразованию сдвига Центр масс системы геометрическая точка, характеризующая движение тела или системы частиц как целого.Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:
где
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.110 (0.014 с.) |

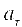 . Она характеризует изменение скорости по модулю.
. Она характеризует изменение скорости по модулю.
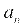 . Она характеризует изменение скорости по направлению.
. Она характеризует изменение скорости по направлению.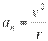

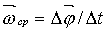
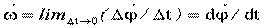 Угловая скорость - величина векторная.
Угловая скорость - величина векторная.
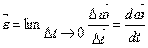
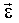 и может совпадать с вектором
и может совпадать с вектором 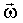 , и быть противоположным ему
, и быть противоположным ему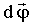 , угловая скорость
, угловая скорость 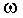 и угловое ускорение
и угловое ускорение 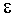 для различных моментов времени t определяется по формулам:
для различных моментов времени t определяется по формулам: 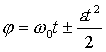
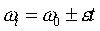
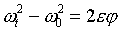
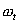 - угловая скорость в данный момент времени t;
- угловая скорость в данный момент времени t; 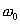 - начальная угловая скорость, при t=0.
- начальная угловая скорость, при t=0.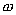 - в (рад /с),
- в (рад /с),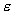 - в (рад /с2).
- в (рад /с2). , а внутренние -
, а внутренние -  .
.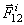 и
и 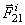 , сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то
, сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то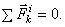 рисунок 3-го закона
рисунок 3-го закона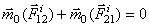 . Аналогичный результат получится при вычислении моментов относительно оси. Следовательно, и для всей системы будет:
. Аналогичный результат получится при вычислении моментов относительно оси. Следовательно, и для всей системы будет: или
или 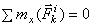 .
.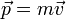 . Си кг/м*с\
. Си кг/м*с\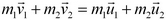
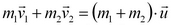

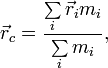
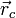 — радиус-вектор центра масс,
— радиус-вектор центра масс, — радиус-вектор i -й точки системы,
— радиус-вектор i -й точки системы,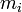 — масса i -й точки.
— масса i -й точки.
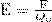 . Си В/м
. Си В/м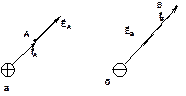 Если электрическое поле создаётся одним точечным зарядом q, то
Если электрическое поле создаётся одним точечным зарядом q, то 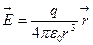 .
.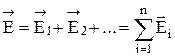 .
.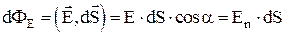 , здесь
, здесь  - угол между векторами
- угол между векторами 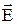 и
и  (нормаль к поверхности dS),
(нормаль к поверхности dS), 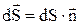 ,
,  - проекция вектора
- проекция вектора 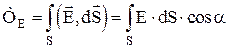 . Таким образом, поток вектора
. Таким образом, поток вектора 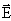 есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным. Теорема Остроградского-Гаусса -поток вектора напряжённости электрического поля в вакууме через любую замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённой на
есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным. Теорема Остроградского-Гаусса -поток вектора напряжённости электрического поля в вакууме через любую замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённой на  .
.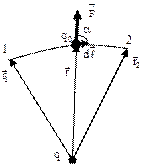 Работа сил электрического поля - Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда. Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Силовые поля, обладающие этим свойством.называют потенциальными или консервативными
Работа сил электрического поля - Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда. Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Силовые поля, обладающие этим свойством.называют потенциальными или консервативными со стороны заряда
со стороны заряда  на элементарном пути dl: dA = F•dl•cosα. По закону Кулона
на элементарном пути dl: dA = F•dl•cosα. По закону Кулона  , dl•cosα = dr. Тогда
, dl•cosα = dr. Тогда 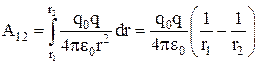 То есть работа определяется только положением точек 1 и 2.
То есть работа определяется только положением точек 1 и 2.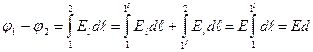 , где d – расстояние между точками 1 и 2 вдоль силовой линии. Итак,
, где d – расстояние между точками 1 и 2 вдоль силовой линии. Итак, 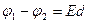 или
или 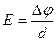
 называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.
называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.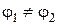 Электри́ческаяпроводи́мость (электропроводность, проводимость) — это способность тела проводить электрический ток, а также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению.
Электри́ческаяпроводи́мость (электропроводность, проводимость) — это способность тела проводить электрический ток, а также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению.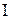 и в СИ измеряется в амперах (A).
и в СИ измеряется в амперах (A). 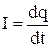 , где dq – заряд, проходящий через поперечное сечение проводника за время dt.
, где dq – заряд, проходящий через поперечное сечение проводника за время dt.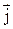 и в СИ измеряется в амперах деленных на квадратный метр (А/м2). Вектор
и в СИ измеряется в амперах деленных на квадратный метр (А/м2). Вектор 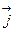 направлен по касательной к линии тока в каждой точке. Направление вектора плотности тока совпадает с направлением упорядоченного движения положительно заряженных частиц.
направлен по касательной к линии тока в каждой точке. Направление вектора плотности тока совпадает с направлением упорядоченного движения положительно заряженных частиц.  . Здесь: е – заряд носителя тока, например, электрона; n – концентрация носителей, т.е. число их в единице объёма проводника;
. Здесь: е – заряд носителя тока, например, электрона; n – концентрация носителей, т.е. число их в единице объёма проводника;  - скорость направленного (упорядоченного) движения носителей заряда.
- скорость направленного (упорядоченного) движения носителей заряда.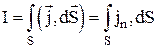 . Это значит, что сила тока
. Это значит, что сила тока 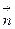 к этому сечению. В дифференциальной форме связь
к этому сечению. В дифференциальной форме связь 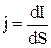 , где dS – площадь сечения, перпендикулярного направлению движения носителей заряда.
, где dS – площадь сечения, перпендикулярного направлению движения носителей заряда.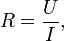 R — сопротивление;
R — сопротивление;
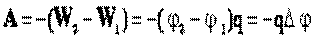 .
. ). В замкнутом контуре (
). В замкнутом контуре (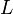 ) тогда ЭДС будет равна:
) тогда ЭДС будет равна:  , где
, где 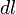 — элемент длины контура.
— элемент длины контура.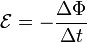
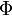 — поток магнитного поля через замкнутую поверхность
— поток магнитного поля через замкнутую поверхность 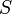 , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).
, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).
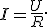
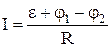 .
.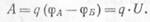
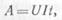
 Окончательная:
Окончательная: 
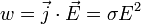 где
где  — мощность выделения тепла в единице объёма,
— мощность выделения тепла в единице объёма, 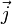 — плотность электрического тока,
— плотность электрического тока,  — напряжённость электрического поля, σ — проводимость среды. В математической форме этот закон имеет вид
— напряжённость электрического поля, σ — проводимость среды. В математической форме этот закон имеет вид
 где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2.
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. , приводит к закону сохранения импульса. Этот закон также соблюдается для изолированных систем. Вследствие однородности пространства и времени движение свободного тела (тело, настолько удаленное от всех окружающих тел, что можно пренебречь его взаимодействием с ними) будет равномерным, т. е. за равные промежутки времени тело должно проходить равные расстояния; оно будет к тому же и прямолинейным. Такое движение свободных тел называют движением по инерции. Движение тел по инерции есть проявление своеобразной симметрии пространства и времени, их однородности.
, приводит к закону сохранения импульса. Этот закон также соблюдается для изолированных систем. Вследствие однородности пространства и времени движение свободного тела (тело, настолько удаленное от всех окружающих тел, что можно пренебречь его взаимодействием с ними) будет равномерным, т. е. за равные промежутки времени тело должно проходить равные расстояния; оно будет к тому же и прямолинейным. Такое движение свободных тел называют движением по инерции. Движение тел по инерции есть проявление своеобразной симметрии пространства и времени, их однородности.


