
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы сохранения импульса и момента импульсаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Законы сохранения импульса и момента импульса Закон сохранения импульса
Механическую систему называют замкнутой или изолированной, если на неё не действуют внешние силы или действие сил компенсируется. Для замкнутой системы сумма всех внешних сил равна нулю
следовательно
а значит
Полученное соотношение – закон сохранения импульса: полный импульс замкнутой системы есть величина постоянная (не меняющаяся с течением времени). Из закона сохранения импульса следует, что внутренние силы системы не могут изменить полного импульса системы. Отдельные тела замкнутой системы могут лишь обмениваться импульсами. При любых процессах, происходящих в замкнутой системе, скорость её центра инерции остается неизменной. Закон сохранения проекции импульса: если в незамкнутой системе сумма проекций внешних сил на некоторое направление равна нулю, то проекция полного импульса системы на это направление остается постоянной. Закон сохранения импульса является одним из основных универсальных законов природы. Он является следствием однородности пространства. Однородность пространства означает, что параллельный перенос в нём замкнутой системы как целого (то есть изменение выбора начала системы координат) не отражается на физических свойствах системы и законах её движения. Закон сохранения момента импульса. Для замкнутой системы момент внешних сил всегда равен нулю, так как на неё внешние силы не действуют, либо их действие скомпенсировано. Поэтому из основного закона динамики вращательного движения вытекает следующий закон, называемый законом сохранения момента импульса: момент импульса замкнутой системы относительно неподвижной точки О не изменяется с течением времени. Вследствие замкнутости системы:
следовательно
Этот закон также справедлив и для момента импульса замкнутой системы относительно любой неподвижной оси ZZ |:
Момент импульса замкнутой системы относительно любой неподвижной оси ZZ|всегда остаётся постоянным. Если система незамкнута, но момент импульса всех внешних сил, действующих на систему, относительно какой-либо неподвижной оси равен нулю, то момент импульса системы относительно этой оси не изменяется с течением времени. Например, если сумма моментов внешних сил относительно оси ZZ|равна нулю, то:
В частности, для тела, вращающегося вокруг неподвижной оси ZZ |:
если
- сумма моментов внешних сил относительно оси ZZ |, где Пример 1. Работа силы тяжести при перемещении тела по наклонной плоскости длины S:

Величина работы A такая же, как если бы тело переместилось по вертикали на h (рис. 3). Таким образом, работа силы тяжести не зависит от формы пути, а определяется только высотой, на которую переместилось тело, т.е. начальным и конечным положением тела. Пример 2. Таким же свойством обладают и упругие силы. Найдём работу, совершаемую при растяжении пружины, подчиняющейся закону Гука:
где x1 – начальное растяжение пружины, x2 – конечное растяжение пружины. Итак, работа упругих сил и сил тяготения не зависит от формы пути, а определяется только начальным и конечным положением точки приложения силы. Такие силы называются консервативными, а поле таких сил – потенциальным. Работа таких сил по замкнутому пути равна нулю. Работа силы трения при перемещении по замкнутому пути не равна нулю. Силы, работа которых не зависит от форм пути, а определяется только координатой начального и конечного положения материальной точки, называются консервативными. Работа таких сил по замкнутому пути равна нулю. Сила трения является неконсервативной – диссипативной. Механическая энергия Состояние тела или системы тел характеризуется величиной, называемой энергия. Энергия – универсальная мера движения различных форм материи и взаимодействий. Существуют различные виды энергии: механическая, тепловая, электромагнитная и т.д. Механическая энергия – это величина, характеризующая максимальную работу, которую тело может совершить. В системе СИ энергия измеряется в джоулях (Дж), как и работа. Если над системой (телом) внешние силы совершают положительную работу (A>0), то это приводит к увеличению энергии. Если работа отрицательна (A<0), то энергия убывает. Иными словами, работа может совершаться только за счет изменения энергии:
т.е. механическая работа – мера изменения механической энергии. Во внешнем силовом поле Если в каждой точке пространства на помещенную туда частицу действует сила, то говорят, что частица находится в поле сил. Например: поле сил тяжести, упругих сил, сил сопротивления и т. д. Если силы, действующие в поле, консервативные, то поле называется потенциальным. Потенциальная энергия – запас работы, обусловленный конфигурацией тел системы (или частей одного тела). Потенциальная энергия может быть только в системе материальных точек, в которой действуют консервативные силы. Потенциальная энергия упругого деформированного тела:
где х – величина деформации. Потенциальная энергия тела в поле тяжести Земли (рис. 8):
где h – высота центра инерции (h << RЗ).
Потенциальная энергия зависит от координат. Она может быть положительной и отрицательной. Начальный уровень отсчета потенциальной энергии можно выбрать произвольно (рис. 9).

Найдем потенциальную энергию тела в поле тяжести Земли (рис. 10). Для больших расстояний между телами из закона всемирного тяготения:
При перемещении тела на
(«минус», так как сила
Потенциальная энергия:
где r – расстояние от поверхности Земли. При
Обычно полагают
Характер зависимости Wп от r указан на рис. 11. В потенциальном поле вводят понятие потенциал:
Потенциал поля тяготения:
где r – расстояние от материальной точки до рассматриваемой точки поля.
Если консервативные силы системы совершают положительную работу, то потенциальная энергия Wп уменьшается, если они совершают отрицательную работу, то Wп растет (при этом положительную работу совершают внешние силы). Зная вид функции Wп (x,y,z), можнонайти консервативную силу, действующую на материальную точку в каждой точке силового поля. Рассмотрим перемещение материальной точки вдоль оси х на dx. При этом над материальной точкой совершается работа:
Эта работа равна убыли потенциальной энергии:
следовательно:
а значит:
Для проекций силы на оси y и z аналогично, следовательно:
Отсюда вектор силы:
Следовательно:
Импульса к столкновениям Процессы столкновения делятся на упругие и неупругие в соответствии с характером изменения внутренней энергии частиц при их взаимодействии. Если внутренняя энергия частиц при этом изменяется, то столкновение называется неупругим, если не изменяется, то столкновение называют упругим. Иногда говорят об абсолютно упругом столкновении, чтобы подчеркнуть, что внутренняя энергия сталкивающихся частиц абсолютно точно неизменна. Говорят также и об абсолютно неупругом столкновении, если в конечном состоянии вся энергия превратилась во внутреннюю. 1. Упругое столкновение. Пусть две частицы массами m1 и m2 движутся в одном направлении, но с разными скоростями, причем V2 > V1 (рис. 12).
Решая совместно уравнения системы (27), найдем скорости U1 и U2 частиц после их столкновения:
Анализируя уравнения (28) и (29), рассмотрим два случая: а) массы частиц одинаковы ( б) масса первой частицы много больше массы второй (m1>>m2), причем она неподвижна (V1=0). Эта ситуация может произойти, например, при столкновении частицы массой m2 с неподвижной стенкой. В таком случает после упругого удара массы m2 стенка останется неподвижной (U1=0), а частица m2 поменяет скорость на противоположную (U2=-V2). 2. Неупругое столкновение. Если частицы массами m1 и m2 претерпевают неупругое центральное столкновение, то их скорости после удара одинаковы, поэтому закон сохранения импульса будет иметь вид:
Скорость
Поскольку при таком столкновении механическая энергия меняется, легко рассчитать ее изменение:
Законы сохранения импульса и момента импульса Закон сохранения импульса
Механическую систему называют замкнутой или изолированной, если на неё не действуют внешние силы или действие сил компенсируется. Для замкнутой системы сумма всех внешних сил равна нулю
следовательно
а значит
Полученное соотношение – закон сохранения импульса: полный импульс замкнутой системы есть величина постоянная (не меняющаяся с течением времени). Из закона сохранения импульса следует, что внутренние силы системы не могут изменить полного импульса системы. Отдельные тела замкнутой системы могут лишь обмениваться импульсами. При любых процессах, происходящих в замкнутой системе, скорость её центра инерции остается неизменной. Закон сохранения проекции импульса: если в незамкнутой системе сумма проекций внешних сил на некоторое направление равна нулю, то проекция полного импульса системы на это направление остается постоянной. Закон сохранения импульса является одним из основных универсальных законов природы. Он является следствием однородности пространства. Однородность пространства означает, что параллельный перенос в нём замкнутой системы как целого (то есть изменение выбора начала системы координат) не отражается на физических свойствах системы и законах её движения. Закон сохранения момента импульса. Для замкнутой системы момент внешних сил всегда равен нулю, так как на неё внешние силы не действуют, либо их действие скомпенсировано. Поэтому из основного закона динамики вращательного движения вытекает следующий закон, называемый законом сохранения момента импульса: момент импульса замкнутой системы относительно неподвижной точки О не изменяется с течением времени. Вследствие замкнутости системы:
следовательно
Этот закон также справедлив и для момента импульса замкнутой системы относительно любой неподвижной оси ZZ |:
Момент импульса замкнутой системы относительно любой неподвижной оси ZZ|всегда остаётся постоянным. Если система незамкнута, но момент импульса всех внешних сил, действующих на систему, относительно какой-либо неподвижной оси равен нулю, то момент импульса системы относительно этой оси не изменяется с течением времени. Например, если сумма моментов внешних сил относительно оси ZZ|равна нулю, то:
В частности, для тела, вращающегося вокруг неподвижной оси ZZ |:
если
- сумма моментов внешних сил относительно оси ZZ |, где
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 2438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.01 с.) |

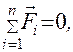
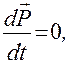

 ,
,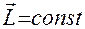 .
.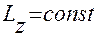 .
.
 .
.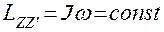 ,
,


 - момент инерции тела относительно оси ZZ |.
- момент инерции тела относительно оси ZZ |. (3)
(3)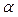
 , (4)
, (4)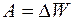 ,
, , (14)
, (14) , (15)
, (15)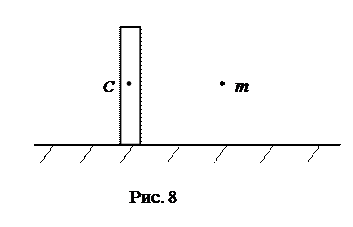

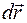 элементарнаяработа силы тяготения:
элементарнаяработа силы тяготения:
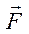 и
и 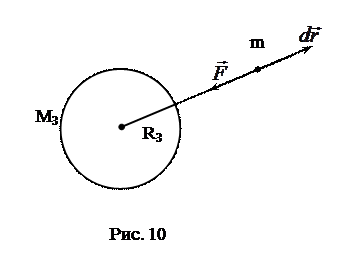
 ,
,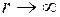 :
:
 , тогда
, тогда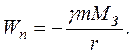 (16)
(16) . (17)
. (17) , (18)
, (18)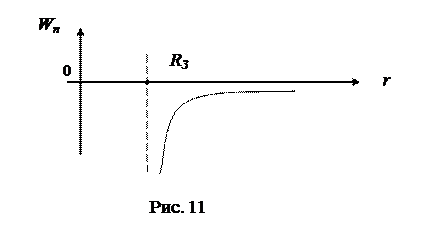

 .
.

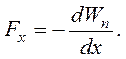
 ,
,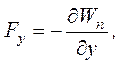


 . (19)
. (19) Тогда, в случае их упругого центрального столкновения, можно записать закон сохранения импульса и закон сохранения механической энергии:
Тогда, в случае их упругого центрального столкновения, можно записать закон сохранения импульса и закон сохранения механической энергии: . (27)
. (27) , (28)
, (28) (29)
(29) ). В этом случае легко убедиться, что после столкновения они просто обменяются скоростями
). В этом случае легко убедиться, что после столкновения они просто обменяются скоростями  и
и  ;
; . (30)
. (30) после столкновения:
после столкновения: (31)
(31) (32)
(32)


