
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия при вращательном и плоском движенияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кинетическая энергия тела, вращающегося вокруг закрепленной оси представляет собой алгебраическую сумму кинетических энергий отдельных его точек:
Таким образом, кинетическая энергия вращающегося тела:
В случае, если центр масс тела движется поступательно со скоростью
где
Пример. Плоское движение – это движение, при котором все точки твердого тела движутся в параллельных плоскостях. Поэтому достаточно рассмотреть движение какого-либо сечения тела в одной плоскости. Рассмотрим скатывание цилиндра с наклонной плоскости. Будем считать, что скатывание происходит без скольжения (рис. 6).
Рис. 6 Уравнение движения для точки С (центр масс цилиндра):
На цилиндр действуют три силы: - сила тяжести - сила нормальной реакции опоры - сила трения Однако, поскольку сила нормальной реакции опоры и сила тяжести приложены к центру масс (точка С), то их моменты относительно оси, проходящей через центр масс, равены нулю, а значит уравнение вращательного движения имеет вид:
Момент инерции цилиндра относительно оси, проходящей через точку С:
Связь углового и линейного ускорений:
Момент силы трения:
Подставим в уравнение вращательного движения (11) выражения для момента инерции, момента силы трения и заменим угловое ускорение Получим:
Таким образом:
Подставляя выражение для силы трения в уравнение (10):
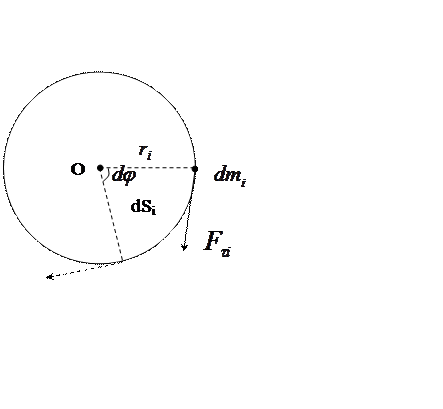
Таким образом, центр инерции цилиндра (т. С) движется с постоянным ускорением а, зависящим только от угла наклона плоскости α. Работа внешних сил при вращательном движении Для получения формулы для работы внешних сил при вращательном движении рассмотрим вначале случай действия на элементарную массу
Рис. 7 Элементарная работа:
или для всего тела:
где М – суммарный момент внешних сил. Если момент силы сонаправлен с угловым перемещением, то работа положительна (A >0). Если момент силы противоположен по направлению вектору углового перемещения, то работа отрицательна (A <0). Таким образом:
Работа внешних сил при вращательном движении затрачивается на изменение кинетической энергии:
где
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 860; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.249 (0.006 с.) |


 (8)
(8)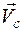 , а все остальные точки этого тела вращаются вокруг оси, проходящей через центр масс, то можно говорить о плоском движении. Полная кинетическая энергия тела:
, а все остальные точки этого тела вращаются вокруг оси, проходящей через центр масс, то можно говорить о плоском движении. Полная кинетическая энергия тела: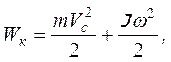 (9)
(9) – момент инерции тела относительно оси, проходящей через центр масс (точка С), перпендикулярно плоскости чертежа (рис. 5)
– момент инерции тела относительно оси, проходящей через центр масс (точка С), перпендикулярно плоскости чертежа (рис. 5)

 . (10)
. (10) ,
, ,
, .
.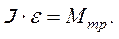 (11)
(11) .
.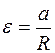 .
. .
. линенйным a.
линенйным a. ,
, .
.
 . (11)
. (11) касательной силы
касательной силы  , которая вызывает ее перемещение по дуге
, которая вызывает ее перемещение по дуге  .
.

 ,
, . (12)
. (12)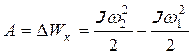 , (13)
, (13) – момент инерции тела относительно неподвижной оси вращения,
– момент инерции тела относительно неподвижной оси вращения,  - начальная и конечная угловые скорости тела.
- начальная и конечная угловые скорости тела.


