
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление кинетической и потенциальной энергий
Получим выражения для кинетической и потенциальной энергий консервативной системы, совершающей малые свободные колебания относительно положения устойчивого равновесия [1,6]. Кинетическая энергия системы в декартовой системе координат может быть записана в виде:
где mi - масса i -й точки. Дифференцируя равенства (2.1.3) по времени, получим компоненты скоростей i -й массы mi в выражении (2.2.1) как функции скоростей обобщенных координат
Подставляя (2.2.2) в (2.2.1), получим
После возведения в квадрат выражений, стоящих в круглых скобках, и изменения порядка суммирования формулу (2.2.3) можно представить в виде:
где Смысл введенных коэффициентов
При малых колебаниях около положения устойчивого равновесия в разложении (2.2.5) можно ограничиться только первым слагаемым и считать
В этом случае выражение для кинетической энергии (2.2.4) можно представить в виде
Таким образом, кинетическая энергия системы с КЧСС при малых колебаниях около положения устойчивого равновесия представляет определенно положительную квадратичную форму от обобщенных скоростей, поскольку в выражении (2.2.1) все слагаемые в сумме больше или равны нулю. В выражении (2.2.7) коэффициенты
Получим выражения для потенциальной энергии, которая для консервативной системы зависит от вектора обобщенных координат
В силу отношений (2.1.22), (2.1.23) первые два слагаемых в (2.2.9) равны нулю, и разложение
где
Потенциальная энергия представляет положительно определенную квадратичную форму обобщенных координат, которую можно представить в матричной форме
2.3. Уравнения малых колебаний консервативных систем относительно устойчивого положения равновесия. Составим уравнение линейных малых колебаний консервативной системы около устойчивого положения равновесия на основе уравнений Лагранжа второго рода (2.1.11). Для этого подставим полученные выражения для кинетической (2.2.7) и потенциальной (2.2.10) энергий в уравнения Лагранжа (2.1.10). В результате получим систему обыкновенных дифференциальных уравнений малых свободных колебаний
Систему (2.3.1) можно записать в матричной форме
Полученные системы представляют системы линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами относительно обобщенных координат
Общее решение систем (2.3.1), (2.3.2) определяет малые свободные линейные колебания системы с КЧСС около положения устойчивого равновесия. Квадратная матрица Предположим, что существует обратная квадратная матрица, которая называется матрицей податливости
Коэффициенты этой матрицы
где E единичная матрица.
Квадратная матрица
Физический смысл системы уравнений (2.3.6) заключается в том, что их можно трактовать как уравнения движения i -й массы, к которой приложены реакции упругих связей
С учетом введенных обозначений (2.3.7) уравнения (2.3.6) можно записать в виде
Система (2.3.8) представляет математическую формулировку принципа Даламбера [6]. Если потенциальная энергия П имеет канонический вид, то матрица жесткости С будет диагональной и уравнение (2.3.1) записывают в обратной форме
Данное уравнение можно разрешить относительно
Таким образом, уравнения в прямой форме можно довольно просто (не обращая матрицы масс и жесткости) разрешить относительно вторых производных от обобщенных координат, а уравнения в обратной форме – относительно обобщенных координат. Прямая и обратная формы записи уравнений движения равноправны. Поэтому ее выбор должен определяться простотой записи уравнений движения и простотой вычисления коэффициентов этих уравнений. Приведением кинетической или потенциальной энергий, представляющих квадратичные формы, к каноническому виду можно добиться значительных упрощений в решении задач теории колебаний. Рассмотрим наиболее часто встречающиеся простые способы для составления уравнений движения определенных классов систем с КЧСС, в которых не используются уравнения Лагранжа [3,11]. На рис.2.3, 2.4 представлены две так называемые цепные системы.
Рисунок 2.3 – Модель системы, совершающей продольные колебания а - дискретная модель б - схема сил, действующих на i -ю массу
Первая система (рис.2.3,а) состоит из сосредоточенных масс mi, соединенных линейно-упругими невесомыми пружинами жесткости ci,и совершает продольные колебания. Вторая система (рис.2.4,а) представляет n массивных дисков с моментами инерции Ii, закрепленных на безмассовом упругом валу, и совершают крутильные колебания. Для данного класса систем рассмотрим так называемый прямой способ составления уравнений движения, который базируется на принципе Даламбера [6].
Рисунок 2.3 – Модель системы, совершающей крутильные колебания а - дискретная модель б - схема моментов, действующих на i -й диск
В соответствии с этим способом необходимо: · задать положение тела, в котором все его координаты имеют положительные значения в соответствии с выбранной системой координат. В данном случае эти перемещения масс · выделить i -ю массу и приложить к ней положительно направленные силы (моменты) (рис.2.3,б; 2.4,б). При этом положительное направление силовых факторов совпадает с положительным направлением осей координат на площадках с положительным направлением внешней нормали. Для площадок с отрицательной внешней нормалью силы (моменты) направлены в отрицательном направлении соответствующих координатных осей;
· в соответствии с принципом Даламбера уравнение движения i -ой массы можно получить, записав сумму всех сил (моментов), действующих на i -ю массу (рис.2.3,б; 2.4,б), включая фиктивные силы инерции В результате суммирования всех сил для первой системы (рис.2.3,а) получим
Система ОДУ описывает малые колебания консервативной системы с КЧСС в прямой форме. В данном случае связи, приложенные к системе, запрещают перемещения дискретных масс в направлении оси Y, а также запрещают перемещения левого конца первой пружины Аналогично для второй системы, совершающей крутильные колебания, уравнения в прямой форме будут иметь вид
Для рассмотренных двух цепных систем, в которых упругие силы зависят только от разности смещений соседних масс, прямая форма записи уравнений движения является более предпочтительной, чем обратная. Для систем, которые не относятся к цепным системам, удобнее применить обратный способ составления уравнений движения [3,11]. К таким системам можно отнести различные стержневые системы, совершающие изгибные колебания. В качестве примера на рис.2.5 представлена невесомая шарнирная балка с двумя сосредоточенными массами m1 и m2. Данный способ заключается в том, что для рассматриваемой системы записывают условия статического равновесия под действием внешних статических возмущающих сил Pi
Рисунок 2.5 – Шарнирная балка
Данные силы Pi при упругом деформировании консервативной системы уравновешиваются обобщенными упругими силами Fi Pi + Fi Упругие силы Fi
Учитывая выражение для потенциальной энергии (2.2.10), из формул (2.3.13) и (2.3.14), получим
Выражение (2.3.15) можно представить в матричной форме:
Равенства (2.3.15) и (2.3.16) являются уравнениями статического равновесия системы в положении, определяемом вектором
где В скалярной форме уравнение (2.3.17) можно представить в виде
При свободных колебаниях в качестве обобщенных сил Pi
или в матричной форме
Полученное матричное уравнение (2.3.20) непосредственно следует из уравнения (2.3.2), если последнее умножить слева на матрицу C-1=D. Однако это уравнение имеет самостоятельное значение в том случае, если матрица податливости D может быть легко получена на основе формул сопротивления материалов (формул Верещагина) [2,3]. Так, например, для системы, изображенной на рис.2.5, матрица податливостей D будет равна
Матрица масс будет диагональной, на главной диагонали которой будут m1 и m2.
Контрольные вопросы: 1. В чем отличие консервативных и диссипативных систем? 2. Почему потенциальная энергия системы представляет положительно определенную квадратичную форму? 3. Какой тип уравнений описывает свободные колебания системы с КЧСС и при каких условиях они должны решаться? 4. Для какого класса механических систем эффективней использовать прямой способ составления уравнений свободных колебаний, а для каких классов обратный? 5. Чем отличаются матрицы жесткостей и податливостей? 3 Свободные колебания систем с конечным числом степеней свободы
3.1 Каноническая форма представления кинетической и потенциальной энергий Нормальные координаты и главные колебания. Как было показано во второй главе, кинетическая Т и потенциальная П энергии системы с КЧСС представляют положительно определенные квадратичные формы. Известно [1,6], что две квадратичные формы
из которых хотя бы одна является положительно определенной, одним линейным преобразованием переменных
можно привести к каноническому виду (сумме квадратов):
При этом все li будут больше нуля li > 0. Продифференцировав выражение (3.1.3), получим связь между векторами обобщенных скоростей
Учитывая эти обстоятельства, кинетическую и потенциальную энергии системы можно записать в виде
Координаты xi(t)
Уравнения (3.1.8), описывающие колебания системы в нормальных (главных) координатах, являются раздельными, поэтому интегрирование каждого уравнения можно выполнить независимо от других. Учитывая, что потенциальная энергия системы, определяемая соотношением (3.1.7), является положительно определенной квадратичной формой, все gi >0
где частоты колебаний
Подставляя решение (3.1.9) в выражение (3.1.3), описывающее гармонические колебания с частотами pi, получим общее выражение для малых колебаний системы
где В соответствии с формулой (3.1.10) компоненты вектора
Полученные выражения (3.1.10) и (3.1.11) описывают всевозможные малые колебания консервативной системы. Если в формулах (3.1.10), (3.1.11) положить все ai=0, кроме i=j, получим в частном случае
Формулы (3.1.12) и (3.1.13) имеют место в случае изменения только j -той нормальной (главной) координаты xi(t), остальные будут равны нулю. Такой ситуации можно добиться путем соответствующего подбора начальных условий. Обобщенные координаты qk(t) Колебания системы, определяемые изменением только одной нормальной (главной) координаты, называются главными или собственными колебаниями, частоты pj, с которыми происходят эти колебания, – собственными частотами системы. В общем случае, когда все
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 705; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.236.219 (0.096 с.) |
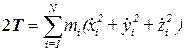 , (2.2.1)
, (2.2.1)
 :
: ,
,  ,
,  ,
,  (2.2.2)
(2.2.2) . (2.2.3)
. (2.2.3)
 (2.2.4)
(2.2.4) .
. , обладающих свойством симметрии
, обладающих свойством симметрии 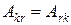 , понятен из приведенных формул (2.2.4). Рассматривая эти коэффициенты как функции обобщенных координат
, понятен из приведенных формул (2.2.4). Рассматривая эти коэффициенты как функции обобщенных координат 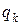 , разложим их в многомерный ряд Тейлора относительно устойчивого положения равновесия
, разложим их в многомерный ряд Тейлора относительно устойчивого положения равновесия 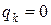
 . (2.2.5)
. (2.2.5) (2.2.6)
(2.2.6) . (2.2.7)
. (2.2.7) называются инерционными коэффициентами, которые образуют симметричную матрицу масс размерностью
называются инерционными коэффициентами, которые образуют симметричную матрицу масс размерностью  и имеют смысл массы или моментов инерции. В матричной форме выражение кинетической энергии (2.2.7) можно представить в виде
и имеют смысл массы или моментов инерции. В матричной форме выражение кинетической энергии (2.2.7) можно представить в виде (2.2.8)
(2.2.8) [1,6]. Для этого разложим потенциальную энергию системы в ряд Тейлора по степеням
[1,6]. Для этого разложим потенциальную энергию системы в ряд Тейлора по степеням  . При малых колебаниях в этом разложении можно ограничиться членами второго порядка малости:
. При малых колебаниях в этом разложении можно ограничиться членами второго порядка малости: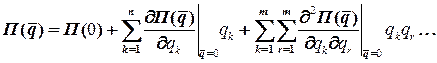 . (2.2.9)
. (2.2.9) начинается с третьего слагаемого
начинается с третьего слагаемого , (2.2.10)
, (2.2.10)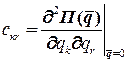 - коэффициенты жесткости, обладающие свойством симметрии
- коэффициенты жесткости, обладающие свойством симметрии  и образующие матрицу жесткости C.
и образующие матрицу жесткости C. (2.2.11)
(2.2.11)
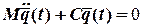 . (2.3.2)
. (2.3.2) ,
,  (2.3.3)
(2.3.3)
 , входящая в уравнения (2.3.2), называется матрицей жесткости, а ее коэффициенты, удовлетворяющие условию симметрии
, входящая в уравнения (2.3.2), называется матрицей жесткости, а ее коэффициенты, удовлетворяющие условию симметрии  , статическими коэффициентами жесткости (коэффициентами жесткости) [3,4]. Коэффициенты
, статическими коэффициентами жесткости (коэффициентами жесткости) [3,4]. Коэффициенты  аналогичны коэффициентам влияния метода перемещений в строительной механике. Они представляют значение силы, которое надо приложить в i -й точке, чтобы получить единичное перемещение в k -й.
аналогичны коэффициентам влияния метода перемещений в строительной механике. Они представляют значение силы, которое надо приложить в i -й точке, чтобы получить единичное перемещение в k -й. (2.3.4)
(2.3.4) , удовлетворяющие также условию симметрии, называются статическими коэффициентами податливости (коэффициенты податливости) [3,4]. Эти коэффициенты аналогичны коэффициентам влияния метода сил в строительной механике и их можно трактовать как перемещение в i -й точке от действия единичной силы, приложенной в k -й точке. Таким образом, матрицы жесткости и податливости являются симметричными и взаимно обратными:
, удовлетворяющие также условию симметрии, называются статическими коэффициентами податливости (коэффициенты податливости) [3,4]. Эти коэффициенты аналогичны коэффициентам влияния метода сил в строительной механике и их можно трактовать как перемещение в i -й точке от действия единичной силы, приложенной в k -й точке. Таким образом, матрицы жесткости и податливости являются симметричными и взаимно обратными: , (2.3.5)
, (2.3.5) называется матрицей масс, а ее коэффициенты
называется матрицей масс, а ее коэффициенты 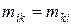 , удовлетворяющие условию симметрии, называются инерционными коэффициентами. Вид матрицы масс зависит от выбора системы обобщенных координат
, удовлетворяющие условию симметрии, называются инерционными коэффициентами. Вид матрицы масс зависит от выбора системы обобщенных координат  , и в простейшем случае ее элементы представляют сосредоточенные массы или моменты инерции. Так, если кинетическая энергия
, и в простейшем случае ее элементы представляют сосредоточенные массы или моменты инерции. Так, если кинетическая энергия  имеет канонический вид, т.е. выражается через сумму коэффициентов скоростей, то матрица масс M является диагональной и дифференциальное уравнение (2.3.1) записывается в прямой форме:
имеет канонический вид, т.е. выражается через сумму коэффициентов скоростей, то матрица масс M является диагональной и дифференциальное уравнение (2.3.1) записывается в прямой форме:
 . (2.3.7)
. (2.3.7)



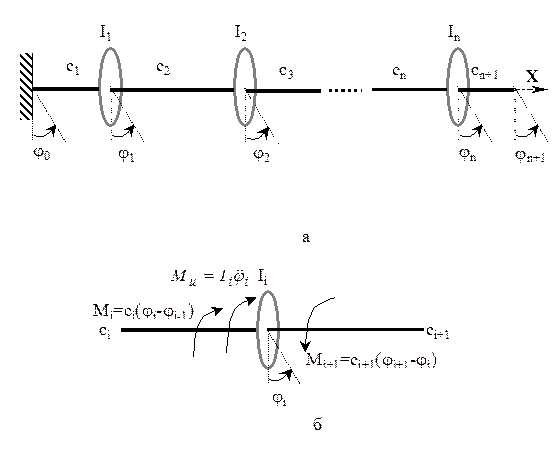
 и углы поворота
и углы поворота 
 в положительном направлении относительно положения равновесия;
в положительном направлении относительно положения равновесия; и
и  . Направление всех указанных сил, приложенных i -й массе, показано на рис.2.3,б; 2.4,б.
. Направление всех указанных сил, приложенных i -й массе, показано на рис.2.3,б; 2.4,б.
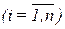 (2.3.11)
(2.3.11) . Отсутствуют силы упругости, приложенные справа от n массы
. Отсутствуют силы упругости, приложенные справа от n массы  .
.


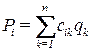
 . (2.3.16)
. (2.3.16) . Уравнение (2.3.16) можно разрешить относительно вектора перемещений
. Уравнение (2.3.16) можно разрешить относительно вектора перемещений  , (2.3.17)
, (2.3.17) – матрица податливостей.
– матрица податливостей.
 , подставляя которые в (2.3.18), получим
, подставляя которые в (2.3.18), получим
 . (2.3.20)
. (2.3.20) , где
, где  (2.3.21)
(2.3.21) ; (3.1.1)
; (3.1.1) , (3.1.2)
, (3.1.2) (3.1.3)
(3.1.3) ; (3.1.4)
; (3.1.4) . (3.1.5)
. (3.1.5) и
и 
 (3.1.6)
(3.1.6) (3.1.7)
(3.1.7)
 (3.1.8)
(3.1.8)
 , амплитуды ai и начальные фазы ji.
, амплитуды ai и начальные фазы ji. , (3.1.10)
, (3.1.10) - вектор, представляющий i -й вектор-столбец матрицы B.
- вектор, представляющий i -й вектор-столбец матрицы B.
 (3.1.11)
(3.1.11)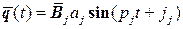 ; (3.1.12)
; (3.1.12)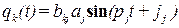
 , описывающие перемещения системы, будут изменяться по одному и тому же гармоническому закону с частотой pj. Система в этом случае совершает гармонические колебания и все ее точки, положение которых определяется координатами qk(t)
, описывающие перемещения системы, будут изменяться по одному и тому же гармоническому закону с частотой pj. Система в этом случае совершает гармонические колебания и все ее точки, положение которых определяется координатами qk(t) 
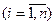 , система с n степенями свободы совершает малые колебания около устойчивого положения равновесия, которые в соответствии с формулой ( 3.1.10 ) представляют линейное наложение n главных (собственных) гармонических колебаний. В этом разложении колебательного процесса, совершаемого системой, на ряд простых гармонических колебаний заключается физический смысл приведения кинетической и потенциальной энергий к каноническому виду.
, система с n степенями свободы совершает малые колебания около устойчивого положения равновесия, которые в соответствии с формулой ( 3.1.10 ) представляют линейное наложение n главных (собственных) гармонических колебаний. В этом разложении колебательного процесса, совершаемого системой, на ряд простых гармонических колебаний заключается физический смысл приведения кинетической и потенциальной энергий к каноническому виду.


