
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия и момент импульса твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Кинетической энергией называется энергия, связанная с движением точки и зависящая от ее скорости. Скорость тела изменяется под действием результирующей силы F. Кинетическая энергия системы точек определяется как сумма кинетических энергий всех точек системы. Изменение кинетической энергии системы равно работе всех сил, действующих на ее точки.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:
Теоремы Кёнига Теорема Кёнига позволяет выразить полную кинетическую энергию системы через энергию движения центра масс и энергию движения относительно центра масс. Формулировка Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс: Вывод Выразим относительную кинетическую энергию Tr системы S как энергию, вычисленной относительно подвижной системы координат. Пусть
Если
Раскрывая скобки и вынося из-под знака интеграла, получаем:
Теоремы Штейнера-Гюйгенса. Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела
Билет №5 Система двух частиц. Приведенная масса. Центральное поле. Законы Кеплера.
Приведенная масса Приведённая масса — условная характеристика распределения масс в движущейся механической или смешанной (например, электро-механической) системе, зависящая от физических параметров системы (масс, моментов инерции, индуктивности и др.) и от её закона движения Обычно приведенная масса
Центральное поле Поле называется центральным, если во всех точках поля векторы напряженности направлены вдоль прямых, которые пересекаются в одной точка, неподвижной по отношению к какой-либо инерциальной системе отсчета. В частности, гравитационное поле материальной точки является центральным: во всех точках поля векторы g и F=mg, действующие на тело, внесенное в гравитационное поле, направлены радиально от массы М, создающей поле, к точечной массе m
Законы Кеплера 1 закон! Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце. Форма эллипса и степень его сходства с окружностью характеризуется отношением Закон Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии. Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца поэклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу. Закон Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.
Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты: Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.
Билет №6 Функция Лагранжа. Уравнения Лагранжа. Обобщенные импульсы, энергия. Цикличе-ские координаты. Функция Гамильтона и уравнения Гамильтона.
Функция Лагранжа Функция Лагранжа- функция L(X,λ), определенная выражением L(X,λ) = F(X) + ∑λiφi(x), где λi - множители Лагранжа. Функция Лагранжа используется при решении задач на условный экстремум. Правило множителей Лагранжа Если x*=(x1,..., xn) - решение задачи на условный экстремум, то существует хотя бы одна ненулевая система множителей Лагранжа λ*(λ1,...,λm) такая, что точка (x*) является точкой стационарности функции Лагранжа по переменным xj и λi, рассматриваемым, как независимые переменные. Метод множителей Лагранжа заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — функции Лагранжа. Уравнения Лагранжа Уравнение Эйлера — Лагранжа Использование уравнений Эйлера — Лагранжа для нахождения экстремума функционала в некотором смысле аналогично использованию теоремы дифференциального исчисления, утверждающей, что лишь в точке, где первая производная функции обращается в нуль, гладкая функция может иметь экстремум (в случае векторного аргумента приравнивается нулю градиент функции, то есть производная по векторному аргументу). Точнее говоря, это прямое обобщение соответствующей формулы на случай функционалов — функций бесконечномерного аргумента. Утверждение Пусть задан функционал Уравнения Лагранжа первого рода Уравнения Лагранжа первого рода — дифференциальные уравнения движения механической системы, записанные в декартовых координатах и содержащие множители Лагранжа. Уравнения Лагранжа первого рода, в некоторых случаях удобно использовать для нахождения реакций связей, если закон движения уже найден каким-либо другим способом (Например с помощью Уравнений Лагранжа второго рода). Уравнения Лагранжа второго рода Уравнениями Лагранжа второго рода называют дифференциальные уравнения движения механической системы, получаемые при применении лагранжева формализма.
Уравнение Д’Аламбера Уравнение Д’Аламбера — дифференциальное уравнение вида
|
||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 , где m - масса тела, V - скорость тела.
, где m - масса тела, V - скорость тела. получим
получим  Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):
Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса): 

 где
где  — полная кинетическая энергия,
— полная кинетическая энергия,  — энергия движения центра масс,
— энергия движения центра масс, 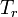 — относительная кинетическая энергия.
— относительная кинетическая энергия. — радиус-вектор рассматриваемой точки в подвижной системе координат. Тогда:
— радиус-вектор рассматриваемой точки в подвижной системе координат. Тогда: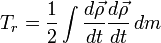
 — радиус-вектор начала координат подвижной системы, а
— радиус-вектор начала координат подвижной системы, а 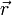 — радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение:
— радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение:  Вычислим полную кинетическую энергию системы в случае, если начало координат подвижной системы помещено в её центр масс. С учетом предыдущего соотношения:
Вычислим полную кинетическую энергию системы в случае, если начало координат подвижной системы помещено в её центр масс. С учетом предыдущего соотношения:
 Первое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно,
Первое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно,  Третий член равен
Третий член равен  относительно произвольной оси равен сумме момента инерции этого тела
относительно произвольной оси равен сумме момента инерции этого тела  относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела
относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела  на квадрат расстояния
на квадрат расстояния  между осями:
между осями: 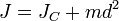 где
где — известный момент инерции относительно оси, проходящей через центр масс тела,
— известный момент инерции относительно оси, проходящей через центр масс тела, — масса тела,
— масса тела, — расстояние между указанными осями.
— расстояние между указанными осями. определяется из равенства
определяется из равенства 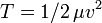 где
где  — скорость той точки системы, к которой приводится масса. В более общем виде приведённая масса является коэффициентом инерции
— скорость той точки системы, к которой приводится масса. В более общем виде приведённая масса является коэффициентом инерции 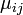 в выражении кинетической энергии системы со стационарными связями, положение которой определяется
в выражении кинетической энергии системы со стационарными связями, положение которой определяется  обобщёнными координатами
обобщёнными координатами 
 где точка означает дифференцирование по времени, а
где точка означает дифференцирование по времени, а 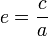 , где
, где  — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),
— расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),  — большая полуось. Величина
— большая полуось. Величина  называется эксцентриситетомэллипса. При
называется эксцентриситетомэллипса. При  и
и 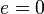 эллипс превращается в окружность
эллипс превращается в окружность , где
, где 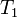 и
и 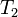 — периоды обращения двух планет вокруг Солнца, а
— периоды обращения двух планет вокруг Солнца, а  и
и  — длины больших полуосей их орбит.
— длины больших полуосей их орбит. , где
, где  — масса Солнца, а
— масса Солнца, а  и
и  — массы планет.
— массы планет. с подынтегральной функцией
с подынтегральной функцией 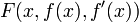 обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом, где через f' обозначена первая производная f по x. Если этот функционал достигает экстремума на некоторой функции
обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом, где через f' обозначена первая производная f по x. Если этот функционал достигает экстремума на некоторой функции  то для неё должно выполняться обыкновенное дифференциальное уравнение
то для неё должно выполняться обыкновенное дифференциальное уравнение 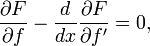 которое называется уравнением Эйлера — Лагранжа.
которое называется уравнением Эйлера — Лагранжа.
 где
где  и
и 


