
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщенные импульсы, энергияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте ОБОБЩЁННЫЕ ИМПУЛЬСЫ, физич. величины рi, определяемые ф-лами: pi=дT/дqi или pi=дL/дqi, где Т — кинетич. энергия, a L — Лагранжа функция данной механич. системы, выраженные через обобщённые координаты qi и обобщённые скорости qi. Размерность О. и. зависит от размерности обобщённой координаты. Если qi имеет размерность длины, то pi — размерность обычного импульса, т. е. произведения массы на скорость; если же координатой qi явл. угол (величина безразмерная), то pi имеет размерность момента кол-ва движения, и т. д. Циклические координаты ЦИКЛИЧЕСКИЕ КООРДИНАТЫ, обобщённые координаты механич. системы, не входящие явно в Лагранжа функцию или в др. характеристич. функции этой системы. Наличие Ц. к. упрощает процесс решения (интегрирования) соответствующих дифф. ур-ний движения механич. системы. Напр., если в ф-ции Лагранжа L не входит явно координата q1; то первое из ур-ний Лагранжа примет вид (d/dt)(дL/дq1)=0 и сразу даёт интеграл дL/дq1=const. Функция Гамильтона и уравнения Гамильтона Функция Гамильтона - характеристическая функция механической системы, выраженная через канонические переменные: обобщенные координаты Уравне́ния Гамильто́на — система дифференциальных уравнений:
где точкой над p и q обозначена производная по времени. Система состоит из 2N дифференциальных уравнений первого порядка (j = 1, 2, …, N) для динамической системы, описываемой N (обобщёнными) координатами, являющихся уравнениями движения (одной из форм таких уравнений, наравне с уравнениями Лагранжа, являющейся обобщением ньютоновских уравнений движения) системы, где Билет №7 Гармонические колебания. Амплитуда. Частота. Пружинный маятник, математический маятник, физический маятник. Гармонические колебания. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, Обобщенное гармоническое колебание в дифференциальном виде
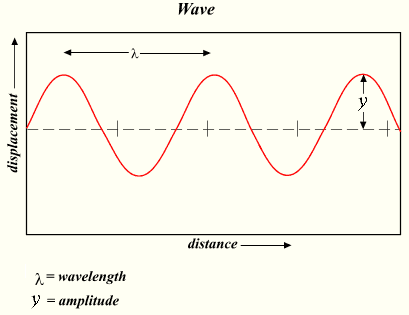
Виды колебаний Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание). Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной). Амплитуда Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины.
Синусоидальное колебание. y — амплитуда волны, λ — длина волны.
Частота Частота колебаний — величина, обратная периоду колебаний, т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени. Разновидность частот колебаний: Циклическая частота- Частота колебаний физического маятника- Частота пружинного маятника- Частота математического маятника- Частота электромагнитных колебаний- Частота колебаний крутильного маятника- Пружинный маятник Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей. В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
Математический маятник Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
Уравнение колебаний маятника Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида Решения уравнения движения
Физический маятник Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести. При небольших углах отклонения (α-мал) физический маятник совершает гармонические колебания. Сила, возвращающая маятник в положение равновесия, представляет собой составляющую силы тяжести, приложенную в точке С: F=mg·sinα. Момент этой силы относительно оси O равен: M=-Fl=-mgd·sinα, где l=d·sinα - плечо силы F относительно оси O, знак минус соответствует тому, что момент M стремится вернуть маятник в положение равновесия, аналогично квазиупругой силе. Циклическая частота ω0=√(mgd/I) Периода колебаний физического маятника T0=2π/ω0=2π√(I/mgd) где d - расстояние от центра тяжести до оси вращения Если период колебаний не зависит от амплитуды, то такие колебания называются изохронными. Мы видим, что малые колебания физического маятника изохронны. Колебания приближенно изохронны, когда угловая амплитуда колебаний не превышает нескольких градусов. При больших амплитудах изохронность нарушается. На свойстве изохронности колебаний маятника основано его применение в часах. Билет №8 Колебания с трением. Диссипативная функция. Диссипативная функция Диссипати́вная функция (функция рассеяния) — функция, вводимая для учёта перехода энергии упорядоченного движения в энергию неупорядоченного движения, в конечном счёте — в тепловую, например, для учёта влияния сил вязкого трения на движение механической системы. Диссипативная функция характеризует степень убывания механической энергии этой системы. Диссипативная функция, делённая на абсолютную температуру, определяет скорость, с которой возрастает энтропия в системе (т. н. производство энтропии). Диссипативная функция имеет размерность мощности Применение понятия Понятие о Диссипативной функции используется при изучении движения диссипативных систем, в частности для учёта влияния сопротивлений на малые колебания системы около её положения равновесия, для исследования затухания колебаний в упругой среде, для учёта тепловых потерь при затухании колебаний электрического тока в системе контуров и др. С учётом диссипации уравнения Лагранжа записываются в виде
Билет №9 Вынужденные колебания без трения. Биения. Резонанс.
|
||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.011 с.) |

 и обобщенные импульсы
и обобщенные импульсы  Для системы со связями, явно не зависящими от времени
Для системы со связями, явно не зависящими от времени  движущейся в стационарном потенциальном силовом поле, функция Гамильтона
движущейся в стационарном потенциальном силовом поле, функция Гамильтона  где П - потенциальная, а Т - кинетическая энергия системы, в выражении которой произведена замена всех обобщенных скоростей
где П - потенциальная, а Т - кинетическая энергия системы, в выражении которой произведена замена всех обобщенных скоростей  Таким образом, функция Гамильтона равна в этом случае полной механической энергии системы, выраженной через
Таким образом, функция Гамильтона равна в этом случае полной механической энергии системы, выраженной через  может быть определена через функцию Лагранжа
может быть определена через функцию Лагранжа  равенством
равенством  в котором все
в котором все  должны быть выражены также через
должны быть выражены также через 

 — так называемая функция Гамильтона, также иногда именуемая гамильтонианом,
— так называемая функция Гамильтона, также иногда именуемая гамильтонианом,  — время
— время  — (обобщенные) координаты
— (обобщенные) координаты  и
и  — обобщенные импульсы
— обобщенные импульсы 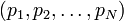 определяющие состояние системы (точку фазового пространства).
определяющие состояние системы (точку фазового пространства). или
или 
 — полная фаза колебаний,
— полная фаза колебаний,  — начальная фаза колебаний.
— начальная фаза колебаний.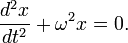 Любое нетривиальное решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой
Любое нетривиальное решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой 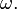







 Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так: — это равнодействующая внешних сил соотнесённая к единице массы груза. В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:
— это равнодействующая внешних сил соотнесённая к единице массы груза. В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c: 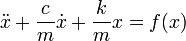
 и не зависит[1] от амплитуды и массы маятника.
и не зависит[1] от амплитуды и массы маятника. где
где  ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция
― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция  ― это угол отклонения маятника в момент от нижнего положения равновесия, выраженный в радианах;
― это угол отклонения маятника в момент от нижнего положения равновесия, выраженный в радианах;  где
где  ― длина подвеса
― длина подвеса  ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:
― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид: 

 где L — функция Лагранжа,
где L — функция Лагранжа,  и
и  — обобщённые координаты и их частные производные по времени, F — диссипативная функция.
— обобщённые координаты и их частные производные по времени, F — диссипативная функция.


