
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон изменения кинетической энергииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Билет №1 Сложение скоростей. ИСО. Законы Ньютона. Силы в природе (трения, тяжести, упру- гости, кулоновская) Сложение скоростей Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
ИСО система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся Законы Ньютона I закон Ньютона Существуют такие системы отсчета, которые называются инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действие других сил скомпенсированно. II закон Ньютона Ускорение тела прямопропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:
III закон Ньютона Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению
Сила трения. Сила, возникающая в месте соприкосновения тел и препятствующая их относительному перемещению, называется силой трения. Направление силы трения противоположно направлению движения. Различают силу трения покоя и силу трения скольжения.
Если тело скользит по какой-либо поверхности, его движению препятствует сила трения скольжения.
Трение покоя – сила трения, препятствующая возникновению движению одного тела по поверхности другого. Сила упругости Сила, возникающая в результате деформации тела и направленная в сторону, противоположную перемещению частиц тела при деформации, называется силой упругости. Деформацию растяжения или сжатия характеризует абсолютное удлинение: Сила упругости, действующая на тело со стороны опоры или подвеса, называется силой реакции опоры (подвеса) или силой натяжения подвеса.
Закон Гука: Сила упругости, возникающая в теле при его деформации растяжения или сжатия, пропорциональна абсолютному удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации:
Сила тяготения. Все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:
Скорость, которую необходимо сообщить телу у поверхности планеты, чтобы оно стало ее спутником, движущимся по круговой орбите, называется первая космическая скорость. Любое тело может стать искусственным спутником другого тела, если сообщить ему необходимую скорость. Сила, с которой тела притягиваются к Земле вследствие гравитационного взаимодействия, называется силой тяжести. Согласно закону всемирного тяготения Весом тела называют силу, с которой тело действует на опору или подвес вследствие притяжения к Земле. Вес тела Р, в отличие от силы тяжести, приложен не к данному телу, а к его опоре или подвесу. Р =mg. Закон Кулона Сила электрического взаимодействия между двумя точечными зарядами в вакууме пропорциональна этим зарядам и обратно пропорциональна квадрату расстояния между ними. При взаимодействии одноименные заряды отталкиваются, разноименные притягиваются. Силы Кулона направлены по прямой, соединяющей заряды Закон Кулона для взаимодействия точечных зарядов Q1 и Q2, находящихся на расстоянии r друг от друга, записывается формулой:
Сила отталкивания F, действующая на заряд Q2 со стороны одноименного заряда Q1, совпадает по направлению с радиусом-вектором r, проведенным из Q1 к этому заряду.
Билет №2 Момент сил. Равновесие тел. Импульс, момент импульса, их законы сохранения и из- менения.
Момент силы Сила приложенная к твердому телу, которое может вращаться вокруг некоторой точки, создает момент силы. Действие момента силы аналогично действию пары сил. Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы. [M]= Ньютон · метр Если: M — момент силы (Ньютон · метр), F — Приложенная сила (Ньютон), r — расстояние от центра вращения до места приложения силы (метр), l — длина перпендикуляра, опущенного из центра вращения на линию действия силы (метр), α — угол, между вектором силы F и вектором положения r, M= F·l= F·r·sin(α) или в виде векторного произведения M=FxR Момент силы — аксиальный вектор. Он направлен вдоль оси вращения Равновесие тел Равновесие тел при отсутствии вращения (линии действия сил пересекаются в одной точке): Векторная сумма всех сил, действующих на тело, равна нулю (алгебраическая сумма проекций всех сил на любую ось равна нулю) Момент силы - равен произведению силы на плечо: Плечо силы - расстояние от оси вращения до линии действия силы. (обозначают буквами ℓ или d). Момент силы, вращающий тело против часовой стрелки, считают положительным, по часовой стрелке - отрицательным. Центр масс - точка, через которую должна проходить линия действия силы, чтобы под действием этой силы тело двигалось поступательно.
Центр тяжести - точка приложения силы тяжести, действующей на тело. В однородном поле тяготения центр тяжести и центр масс совпадают. Равновесие тел при отсутствии вращения (линии действия сил не пересекаются в одной точке): 1. Векторная сумма всех сил, действующих на тело, равна нулю; 2. Алгебраическая сумма моментов всех сил, действующих на тело, относительно любой точки равна нулю.
Импульс Импульс тела - это физическая векторная величина, равная произведению массы тела на его скорость. Момент импульса Момент импульса L частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов: Законы сохранения импульса В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Для 3-го закона Ньютона Для 2-го закона Ньютона
Билет №3 Работа, мощность, энергия. Закон изменения кинетической энергии. Закон сохранения и изменения полной механической энергии. Работа В физике "механической работой" называют работу какой-нибудь силы (силы тяжести, упругости, трения и т.д.) над телом, в результате действия которой тело перемещается.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения:
Здесь точкой обозначено скалярное произведение, Если сила не постоянна, то в этом случае она вычисляется как интеграл: Если существует зависимость силы от координат интеграл определяется следующим образом:
Мощность
Мощность показывает, какая работа совершается за единицу времени. Единица мощности называется Ватт (Вт)
На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств.
Энергия Энергия- универсальная мера различных форм движения и взаимодействия материи. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной вторым телом. Билет №4 Вращательное движение. Момент импульса. Тензор инерции. Кинетическая энергия и момент импульса твердого тела. Теоремы Кёнига и Штейнера-Гюйгенса.
Вращательное движение. Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна. Частота вращения — число оборотов тела в единицу времени. Период вращения — время одного полного оборота. Период вращения T и его частота Линейная скорость точки, находящейся на расстоянии R от оси вращения Угловая скорость вращения тела Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: Кинетическая энергия вращательного движения
Момент импульса Момент импульса L частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов: Тензор инерции Тензор инерции — в механике абсолютно твёрдого тела — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью:
Тензор инерции любого тела зависит от точки, относительно которой он рассчитан. Обычно выделенную роль играет тензор инерции относительно центра масс тела (тогда p в третьей формуле — это просто импульс тела). Также может быть удобно пользоваться моментом инерции, рассчитанным относительно закрепленной (неподвижной) точки тела или точки, находящейся на закреплённой оси вращения. Пересчёт тензора инерции для нового центра, зная его относительно старого, позволяет легко осуществить теорема Штейнера (она же позволяет сделать это и в виде пересчёта, например, формулы кинетической энергии, позволяя, таким образом, оперировать только тензором инерции относительно центра масс).
Как и любой симметричный тензор, тензор инерции может быть диагонализован, то есть можно найти три ортогональные оси координат (собственные оси, орты которых являются собственными векторами и образуют собственный базис тензора инерции) — жестко связанные, конечно, с твёрдым телом, — в которых матрица тензора инерции диагональна, и её собственные числа (собственные числа тензора инерции) определяют главные моменты инерции тела.
Нетрудно видеть, что главные моменты инерции совпадают с осевыми моментами инерции относительно главных осей:
Теоремы Кёнига Теорема Кёнига позволяет выразить полную кинетическую энергию системы через энергию движения центра масс и энергию движения относительно центра масс. Формулировка Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс: Вывод Выразим относительную кинетическую энергию Tr системы S как энергию, вычисленной относительно подвижной системы координат. Пусть
Если
Раскрывая скобки и вынося из-под знака интеграла, получаем:
Теоремы Штейнера-Гюйгенса. Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела
Билет №5 Система двух частиц. Приведенная масса. Центральное поле. Законы Кеплера.
Приведенная масса Приведённая масса — условная характеристика распределения масс в движущейся механической или смешанной (например, электро-механической) системе, зависящая от физических параметров системы (масс, моментов инерции, индуктивности и др.) и от её закона движения Обычно приведенная масса
Центральное поле Поле называется центральным, если во всех точках поля векторы напряженности направлены вдоль прямых, которые пересекаются в одной точка, неподвижной по отношению к какой-либо инерциальной системе отсчета. В частности, гравитационное поле материальной точки является центральным: во всех точках поля векторы g и F=mg, действующие на тело, внесенное в гравитационное поле, направлены радиально от массы М, создающей поле, к точечной массе m
Законы Кеплера 1 закон! Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце. Форма эллипса и степень его сходства с окружностью характеризуется отношением Закон Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии. Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца поэклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу. Закон Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.
Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты: Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.
Билет №6 Функция Лагранжа. Уравнения Лагранжа. Обобщенные импульсы, энергия. Цикличе-ские координаты. Функция Гамильтона и уравнения Гамильтона.
Функция Лагранжа Функция Лагранжа- функция L(X,λ), определенная выражением L(X,λ) = F(X) + ∑λiφi(x), где λi - множители Лагранжа. Функция Лагранжа используется при решении задач на условный экстремум. Правило множителей Лагранжа Если x*=(x1,..., xn) - решение задачи на условный экстремум, то существует хотя бы одна ненулевая система множителей Лагранжа λ*(λ1,...,λm) такая, что точка (x*) является точкой стационарности функции Лагранжа по переменным xj и λi, рассматриваемым, как независимые переменные. Метод множителей Лагранжа заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — функции Лагранжа. Уравнения Лагранжа Уравнение Эйлера — Лагранжа Использование уравнений Эйлера — Лагранжа для нахождения экстремума функционала в некотором смысле аналогично использованию теоремы дифференциального исчисления, утверждающей, что лишь в точке, где первая производная функции обращается в нуль, гладкая функция может иметь экстремум (в случае векторного аргумента приравнивается нулю градиент функции, то есть производная по векторному аргументу). Точнее говоря, это прямое обобщение соответствующей формулы на случай функционалов — функций бесконечномерного аргумента. Утверждение Пусть задан функционал Уравнения Лагранжа первого рода Уравнения Лагранжа первого рода — дифференциальные уравнения движения механической системы, записанные в декартовых координатах и содержащие множители Лагранжа. Уравнения Лагранжа первого рода, в некоторых случаях удобно использовать для нахождения реакций связей, если закон движения уже найден каким-либо другим способом (Например с помощью Уравнений Лагранжа второго рода). Уравнения Лагранжа второго рода Уравнениями Лагранжа второго рода называют дифференциальные уравнения движения механической системы, получаемые при применении лагранжева формализма.
Уравнение Д’Аламбера Уравнение Д’Аламбера — дифференциальное уравнение вида Циклические координаты ЦИКЛИЧЕСКИЕ КООРДИНАТЫ, обобщённые координаты механич. системы, не входящие явно в Лагранжа функцию или в др. характеристич. функции этой системы. Наличие Ц. к. упрощает процесс решения (интегрирования) соответствующих дифф. ур-ний движения механич. системы. Напр., если в ф-ции Лагранжа L не входит явно координата q1; то первое из ур-ний Лагранжа примет вид (d/dt)(дL/дq1)=0 и сразу даёт интеграл дL/дq1=const. Билет №7 Гармонические колебания. Амплитуда. Частота. Пружинный маятник, математический маятник, физический маятник. Гармонические колебания. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, Обобщенное гармоническое колебание в дифференциальном виде
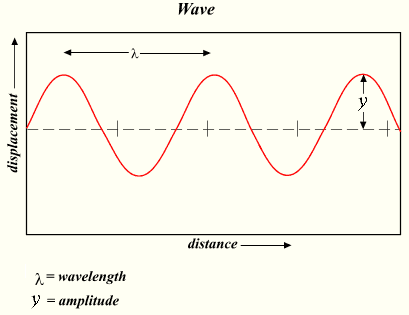
Виды колебаний Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание). Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной). Амплитуда Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины.
Синусоидальное колебание. y — амплитуда волны, λ — длина волны.
Частота Частота колебаний — величина, обратная периоду колебаний, т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени. Разновидность частот колебаний: Циклическая частота- Частота колебаний физического маятника- Частота пружинного маятника- Частота математического маятника- Частота электромагнитных колебаний- Частота колебаний крутильного маятника- Пружинный маятник Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей. В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
Математический маятник Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
Уравнение колебаний маятника Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида Решения уравнения движения
Физический маятник Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести. При небольших углах отклонения (α-мал) физический маятник совершает гармонические колебания. Сила, возвращающая маятник в положение равновесия, представляет собой составляющую силы тяжести, приложенную в точке С: F=mg·sinα. Момент этой силы относительно оси O равен: M=-Fl=-mgd·sinα, где l=d·sinα - плечо силы F относительно оси O, знак минус соответствует тому, что момент M стремится вернуть маятник в положение равновесия, аналогично квазиупругой силе. Циклическая частота ω0=√(mgd/I) Периода колебаний физического маятника T0=2π/ω0=2π√(I/mgd) где d - расстояние от центра тяжести до оси вращения Если период колебаний не зависит от амплитуды, то такие колебания называются изохронными. Мы видим, что малые колебания физического маятника изохронны. Колебания приближенно изохронны, когда угловая амплитуда колебаний не превышает нескольких градусов. При больших амплитудах изохронность нарушается. На свойстве изохронности колебаний маятника основано его применение в часах. Билет №8 Колебания с трением. Диссипативная функция. Диссипативная функция Диссипати́вная функция (функция рассеяния) — функция, вводимая для учёта перехода энергии упорядоченного движения в энергию неупорядоченного движения, в конечном счёте — в тепловую, например, для учёта влияния сил вязкого трения на движение механической системы. Диссипативная функция характеризует степень убывания механической энергии этой системы. Диссипативная функция, делённая на абсолютную температуру, определяет скорость, с которой возрастает энтропия в системе (т. н. производство энтропии). Диссипативная функция имеет размерность мощности Применение понятия Понятие о Диссипативной функции используется при изучении движения диссипативных систем, в частности для учёта влияния сопротивлений на малые колебания системы около её положения равновесия, для исследования затухания колебаний в упругой среде, для учёта тепловых потерь при затухании колебаний электрического тока в системе контуров и др. С учётом диссипации уравнения Лагранжа записываются в виде
|
||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.017 с.) |


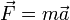

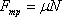 где N — сила реакции опоры, a μ — коэффициент трения скольжения. Коэффициент μ зависит от материала и качества обработки соприкасающихся поверхностей и не зависит от веса тела. Коэффициент трения определяется опытным путем.
где N — сила реакции опоры, a μ — коэффициент трения скольжения. Коэффициент μ зависит от материала и качества обработки соприкасающихся поверхностей и не зависит от веса тела. Коэффициент трения определяется опытным путем. где х0 — первоначальная длина образца, х — его длина в деформированном состоянии. Относительным удлинением тела называют отношение
где х0 — первоначальная длина образца, х — его длина в деформированном состоянии. Относительным удлинением тела называют отношение 
 Здесь х – удлинение тела (пружины) (м). Удлинение положительно при растяжении тела и отрицательно при сжатии.
Здесь х – удлинение тела (пружины) (м). Удлинение положительно при растяжении тела и отрицательно при сжатии. Коэффициент пропорциональности G называется гравитационной постоянной
Коэффициент пропорциональности G называется гравитационной постоянной где g – ускорение свободного падения на планете, R – радиус планеты. Для Земли первая космическая скорость составляет приблизительно 7,9 км/с.
где g – ускорение свободного падения на планете, R – радиус планеты. Для Земли первая космическая скорость составляет приблизительно 7,9 км/с. или
или  где g — ускорение свободного падения, R — расстояние от центра Земли до тела, М — масса Земли, т — масса тела.
где g — ускорение свободного падения, R — расстояние от центра Земли до тела, М — масса Земли, т — масса тела.

 или
или 

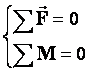

 где r — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, P — импульс частицы.
где r — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, P — импульс частицы. где
где  — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.


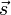 — вектор перемещения; подразумевается, что действующая сила
— вектор перемещения; подразумевается, что действующая сила  постоянна в течение всего того времени, за которое вычисляется работа.
постоянна в течение всего того времени, за которое вычисляется работа.
 где
где  и
и  — радиус-векторы начального и конечного положения тела соответственно.
— радиус-векторы начального и конечного положения тела соответственно. Мощность– физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа.
Мощность– физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа. эта формула справедлива для равномерного движения с постоянной скоростью и в случае переменного движения для средней скорости.
эта формула справедлива для равномерного движения с постоянной скоростью и в случае переменного движения для средней скорости. Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот.
Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот.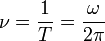
 связаны соотношением
связаны соотношением 


 где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
где: mi — масса i-й точки, ri — расстояние от i-й точки до оси. где Iz — момент инерции тела относительно оси вращения.
где Iz — момент инерции тела относительно оси вращения.  — угловая скорость
— угловая скорость где
где  — тензор инерции,
— тензор инерции,  — угловая скорость,
— угловая скорость,  — момент импульса
— момент импульса
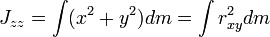
 где
где  — полная кинетическая энергия,
— полная кинетическая энергия,  — энергия движения центра масс,
— энергия движения центра масс, 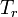 — относительная кинетическая энергия.
— относительная кинетическая энергия. — радиус-вектор рассматриваемой точки в подвижной системе координат. Тогда:
— радиус-вектор рассматриваемой точки в подвижной системе координат. Тогда: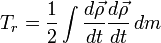
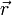 — радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение:
— радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение:  Вычислим полную кинетическую энергию системы в случае, если начало координат подвижной системы помещено в её центр масс. С учетом предыдущего соотношения:
Вычислим полную кинетическую энергию системы в случае, если начало координат подвижной системы помещено в её центр масс. С учетом предыдущего соотношения:
 Первое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно,
Первое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно,  Третий член равен
Третий член равен  относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела
относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела  на квадрат расстояния
на квадрат расстояния  между осями:
между осями: 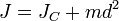 где
где — известный момент инерции относительно оси, проходящей через центр масс тела,
— известный момент инерции относительно оси, проходящей через центр масс тела, — масса тела,
— масса тела, — расстояние между указанными осями.
— расстояние между указанными осями. определяется из равенства
определяется из равенства 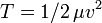 где
где  — скорость той точки системы, к которой приводится масса. В более общем виде приведённая масса является коэффициентом инерции
— скорость той точки системы, к которой приводится масса. В более общем виде приведённая масса является коэффициентом инерции 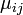 в выражении кинетической энергии системы со стационарными связями, положение которой определяется
в выражении кинетической энергии системы со стационарными связями, положение которой определяется  обобщёнными координатами
обобщёнными координатами 
 где точка означает дифференцирование по времени, а
где точка означает дифференцирование по времени, а 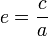 , где
, где  — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),
— расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),  — большая полуось. Величина
— большая полуось. Величина  называется эксцентриситетомэллипса. При
называется эксцентриситетомэллипса. При  и
и 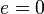 эллипс превращается в окружность
эллипс превращается в окружность , где
, где 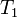 и
и 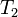 — периоды обращения двух планет вокруг Солнца, а
— периоды обращения двух планет вокруг Солнца, а  и
и  — длины больших полуосей их орбит.
— длины больших полуосей их орбит. , где
, где  — масса Солнца, а
— масса Солнца, а  и
и  — массы планет.
— массы планет. с подынтегральной функцией
с подынтегральной функцией 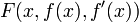 обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом, где через f' обозначена первая производная f по x. Если этот функционал достигает экстремума на некоторой функции
обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом, где через f' обозначена первая производная f по x. Если этот функционал достигает экстремума на некоторой функции  то для неё должно выполняться обыкновенное дифференциальное уравнение
то для неё должно выполняться обыкновенное дифференциальное уравнение 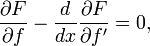 которое называется уравнением Эйлера — Лагранжа.
которое называется уравнением Эйлера — Лагранжа.
 где
где  и
и  или
или 
 — полная фаза колебаний,
— полная фаза колебаний, 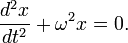 Любое нетривиальное решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой
Любое нетривиальное решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой 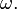







 Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так: — это равнодействующая внешних сил соотнесённая к единице массы груза. В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:
— это равнодействующая внешних сил соотнесённая к единице массы груза. В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c: 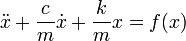
 и не зависит[1] от амплитуды и массы маятника.
и не зависит[1] от амплитуды и массы маятника. где
где  ― это угол отклонения маятника в момент от нижнего положения равновесия, выраженный в радианах;
― это угол отклонения маятника в момент от нижнего положения равновесия, выраженный в радианах;  где
где  ― длина подвеса
― длина подвеса  ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:
― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид: 

 где L — функция Лагранжа,
где L — функция Лагранжа,  и
и  — обобщённые координаты и их частные производные по времени, F — диссипат
— обобщённые координаты и их частные производные по времени, F — диссипат 


