
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Всемирный закон тяготения. Сила тяжести и вес тела.Содержание книги
Поиск на нашем сайте Между любыми двумя материальными точками действуют силы взаимного притяжения, прямо пропорциональные произведению масс этих точек и обратно пропорциональные квадрату расстояния между ними F12 = g (m1m2/R2) R12/R, где F12 - сила тяготения, действующая на точку с массой m1, R12 - радиус-вектор, проведенный из этой точки в точку, обладающую массой m2, R = |R12| - расстояние между точками. Коэффициент g называется гравитационной постоянной (постоянной тяготения). Он численно равен силе взаимного притяжения между двумя материальными точками, которые обладают одинаковыми массами, равными единице массы, и находятся друг от друга на расстоянии, равном единице длины. Гравитационная постоянная определяется опытным путем. Ее численное значение зависит только от выбора системы единиц измерения: g = 6.67*10-11 Н*м2/кг2 = g = 6.67*10-8 дин*см2/г2 По третьему закону Ньютона сила F21 действующая па материальную точку с массой m2 численно равна силе F12, но направлена в противоположную сторону: F12 = - F21 Весом тела называется сила Р, с которой неподвижное относительно Земли тело давит на опору вследствие притяжения его к Земле. Вес тела равен векторной разности силы F тяготения тела к Земле и центростремительной силы Fц обусловливающей участие тела в суточном вращении Земли: P = F – Fц причем Fц = mw2 Rcos f, где m - масса тела, w - угловая скорость суточного вращения Земли, R - радиус Земли, а f - географическая широта места наблюдения А. Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если М – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна
Упругие силы. Модуль Юнга. При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости. Простейшим видом деформации является деформация растяжения или сжатия. При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации: Fx = Fупр = –kx. Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ: 6. Теорема об изменении импульса тела и системы. Закон сохранения импульса.
Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны m 1, m 2,.... mn, и v1, v2,..., v n. Пусть Складывая почленно эти уравнения, получаем
Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то
или
7. Центр масс механической системы. В механике Галилея—Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С,положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен Учитывая, что pi = mi v i, a Подставив выражение в уравнение, получим Из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным. 8. Уравнение движения тела переменной массы. Уравнение Циолковского. Движение некоторых тел сопровождается изменением их массы, например масса ракеты уменьшается вследствие истечения газов, образующихся при сгорании топлива, и т. п. Выведем уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты m, а ее скорость v, то по истечении времени d t ее масса уменьшится на d m и станет равной т — d m, а скорость станет равной v + dv. Изменение импульса системы за отрезок времени d t (учли, что d m dv — малый высшего порядка малости по сравнению с остальными). Если на систему действуют внешние силы, то dp=Fd t, поэтому Полагая F=0 и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса m 0, то С = u ln(m 0). Следовательно, v = u ln (m 0/ m). Это соотношение называется формулой Циолковского. Она показывает, что: 1) чем больше конечная масса ракеты т, тем больше должна быть стартовая масса ракеты m 0; 2) чем больше скорость истечения и газов, тем больше может быть конечная масса при данной стартовой массе ракеты.
9. Работа и мощность. Кинетическая энергия. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs = F cos), умноженной на перемещение точки приложения силы: Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная. Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с). Кинетическая энергия механической системы — это энергия механического движения этой системы. Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа d A силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии d T тела, т. е. 10. Консервативные силы. Потенциальная энергия. Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, — консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является сила трения. Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:
12. Абсолютно неупругий и упругий удары. Удар (или соударение)—это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Если для сталкивающихся тел e (коэффициент восстановления)=0, то такие тела называются абсолютно неупругими, если e=1 — абсолютно упругими. Абсолютно упругий удар — столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию (подчеркнем, что это идеализированный случай). Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии. Обозначим скорости шаров массами т 1 и m 2 до удара через v1 и v2, после удара—через Находим Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу (рис. 22). Если массы шаров т 1 и т 2, их скорости до удара v1 и v2, то, используя закон сохранения импульса, можно записать
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.008 с.) |

 где g – ускорение свободного падения у поверхности Земли:
где g – ускорение свободного падения у поверхности Земли: 
 Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах.
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах. Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются — внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т. е. геометрическая сумма внутренних сил равна нулю.
Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются — внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т. е. геометрическая сумма внутренних сил равна нулю. — равнодействующие внутренних сил, действующих на каждое из этих тел, a
— равнодействующие внутренних сил, действующих на каждое из этих тел, a  — равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:
— равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы: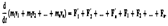

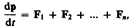 где
где  — импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему. В случае отсутствия внешних сил (рассматриваем замкнутую систему)
— импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему. В случае отсутствия внешних сил (рассматриваем замкнутую систему) Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. где mi и ri — соответственно масса и радиус-вектор i -й материальной точки; n — число материальных точек в системе;
где mi и ri — соответственно масса и радиус-вектор i -й материальной точки; n — число материальных точек в системе; 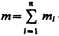 – масса системы. Скорость центра масс
– масса системы. Скорость центра масс 
 есть импульс р системы, можно написать
есть импульс р системы, можно написать 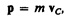 т. е. импульс системы равен произведению массы системы на скорость ее центра масс.
т. е. импульс системы равен произведению массы системы на скорость ее центра масс. т. е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе. Выражение представляет собойзакон движения центра масс.
т. е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе. Выражение представляет собойзакон движения центра масс. где u — скорость истечения газов относительно ракеты. Тогда
где u — скорость истечения газов относительно ракеты. Тогда 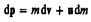
 или
или 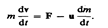 Второе слагаемое в правой части (10.1) называют реактивной силой Fp. Если u противоположен v по направлению, то ракета ускоряется, а если совпадает с v, то тормозится. Таким образом, мы получили уравнение движения тела переменной массы
Второе слагаемое в правой части (10.1) называют реактивной силой Fp. Если u противоположен v по направлению, то ракета ускоряется, а если совпадает с v, то тормозится. Таким образом, мы получили уравнение движения тела переменной массы  .
. откуда
откуда 
 (11.1) В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения — прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина
(11.1) В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения — прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина  где — угол между векторами F и dr; ds = |dr| — элементарный путь; Fs — проекция вектора F на вектор dr (рис. 13).
где — угол между векторами F и dr; ds = |dr| — элементарный путь; Fs — проекция вектора F на вектор dr (рис. 13). (11.2). Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н × м). Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
(11.2). Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н × м). Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:  За время d t силаF совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени
За время d t силаF совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени 
 Используя второй закон Ньютона
Используя второй закон Ньютона  и умножая на перемещение dr получаем
и умножая на перемещение dr получаем  Так как
Так как 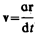 то d A = mv d v =mvdv= d T, откуда
то d A = mv d v =mvdv= d T, откуда  Таким образом, тело массой т, движущееся со скоростью v, обладает кинетической энергией
Таким образом, тело массой т, движущееся со скоростью v, обладает кинетической энергией  (12.1) Из формулы (12.1) видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения. При выводе формулы (12.1) предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать законы Ньютона. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.
(12.1) Из формулы (12.1) видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения. При выводе формулы (12.1) предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать законы Ньютона. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета. (12.2) Работа d A выражается как скалярное произведение силы F на перемещение dr и выражение (12.2) можно записать в виде
(12.2) Работа d A выражается как скалярное произведение силы F на перемещение dr и выражение (12.2) можно записать в виде (12.3) Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу F по модулю и направлению. Потенциальная энергия может быть определена исходя из (12.3) как
(12.3) Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу F по модулю и направлению. Потенциальная энергия может быть определена исходя из (12.3) как  где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня. Для консервативных сил
где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня. Для консервативных сил или в векторном виде
или в векторном виде  (12.4) где
(12.4) где (12.5) (i, j, k — единичные векторы координатных осей). Вектор, определяемый выражением (12.5), называется градиентом скаляра П.
(12.5) (i, j, k — единичные векторы координатных осей). Вектор, определяемый выражением (12.5), называется градиентом скаляра П.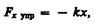 где Fx упp — проекция силы упругости на ось х; k — коэффициент упругости (для пружины — жесткость), а знак минус указывает, что Fx упpнаправлена в сторону, противоположную деформации x. По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е.
где Fx упp — проекция силы упругости на ось х; k — коэффициент упругости (для пружины — жесткость), а знак минус указывает, что Fx упpнаправлена в сторону, противоположную деформации x. По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е.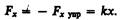 Элементарная работа d A, совершаемая силой Fx при бесконечно малой деформации d x, равна
Элементарная работа d A, совершаемая силой Fx при бесконечно малой деформации d x, равна а полная работа
а полная работа  идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела
идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела 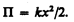

 и
и 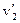 (рис. 18). В случае прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. Их направления учтем знаками: положительное значение припишем движению вправо, отрицатель-нос — движению влево.
(рис. 18). В случае прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. Их направления учтем знаками: положительное значение припишем движению вправо, отрицатель-нос — движению влево.

 где v — скорость движения шаров после удара. Тогда
где v — скорость движения шаров после удара. Тогда (15.10) Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае, если массы шаров равны (т 1= т 2), то
(15.10) Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае, если массы шаров равны (т 1= т 2), то  Абсолютно неупругий удар — пример того, как происходит «потеря» механической энергии под действием диссипативных сил.
Абсолютно неупругий удар — пример того, как происходит «потеря» механической энергии под действием диссипативных сил.


