
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диполь. Потенциал поля диполя.Содержание книги
Поиск на нашем сайте
Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q,–Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя 1. Вектор Согласно принципу суперпозиции, напряженность Е поля диполя в произвольной точке где Е+ и Е– — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряженность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси. Во внешнем электрическом поле на диполь действует момент сил, который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля. Потенциальная энергия диполя в электрическом поле равна
43. Диэлектрики и их типы и поляризация. Диэлектрик (как и всякое вещество) состоит из атомов и молекул. Так как положительный заряд всех ядер молекулы равен суммарному заряду электронов, то молекула в целом электрически нейтральна. Если заменить положительные заряды ядер молекул суммарным зарядом + Q, находящимся в центре «тяжести» положительных зарядов, а заряд всех электронов — суммарным отрицательным зарядом – Q, находящимся в центре «тяжести» отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом. Первую группу диэлектриков (N2, Н2, О2, СО2, СН4,...) составляют вещества, молекулы которых имеют симметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и, следовательно, дипольный момент молекулы р равен нулю. Молекулы таких диэлектриков называются неполярными. Вторую группу диэлектриков (H2O, NН3, SO2, CO,...) составляют вещества, молекулы которых имеют асимметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов не совпадают. Таким образом, эти молекулы в отсутствие внешнего электрического поля обладают дипольным моментом. Молекулы таких диэлектриков называются полярными. При отсутствии внешнего поля, однако, дипольные моменты полярных молекул вследствие теплового движения ориентированы в пространстве хаотично и их результирующий момент равен нулю. Третью группу диэлектриков (NaCl, KCl, КВr,...) составляют вещества, молекулы которых имеют ионное строение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. Таким образом, внесение всех трех групп диэлектриков во внешнее электрическое поле приводит к возникновению отличного от нуля результирующего электрического момента диэлектрика, или, иными словами, к поляризации диэлектрика. Поляризацией диэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей. Соответственно трем группам диэлектриков различают три вида поляризации: электронная, или деформационная, поляризация диэлектрика с неполярными молекулами, заключающаяся в возникновении у атомов индуцированного дипольного момента за счет деформации электронных орбит; ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура; ионная поляризация диэлектриков с ионными кристаллическими решетками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных — против поля, приводящем к возникновению дипольных моментов. Для количественного описания поляризации диэлектрика пользуются векторной величиной — поляризованностью, определяемой как дипольный момент единицы объема диэлектрика:
44. Формы теоремы Гаусса. Вектор электрического смещения. Безразмерная величина Вектор электрической индукции D (называемый также электрическим смещением) является суммой двух векторов различной природы: напряжённости электрического поля Е - главной характеристики этого поля - и поляризации Р, которая определяет электрическое состояние вещества в этом поле. В системе Гаусса: D = e0E + P, где e0 - размерная константа, называемая электрической постоянной или диэлектрической проницаемостью вакуума. Теорема Гаусса для электростатического поля в диэлектрике: Для вакуума Dn = e 0 En (e =1), тогда поток вектора напряженности Е сквозь произвольную замкнутую поверхность равен
45. ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ СОСТАВЛЯЮЩИХ ВЕКТОРОВ Е и Д. Рассмотрим связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых e1 и e2) при отсутствии на границе свободных зарядов. Построим вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l, ориентировав его так, как показано на рис. 136. Согласно теоремео циркуляции вектора Е,
46. ЭЛЕКТРОЕМКОСТЬ ПРОВОДНИКА И КОНДЕНСАТОРА. Рассмотримуединенный проводник, т. е. проводник, который удален от других проводников, тел и зарядов. Его потенциал, согласно (84.5), прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, имеют различные потенциалы. Поэтому для уединенного проводника можно записать На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов. Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (j1 — j2) между его обкладками:
47. ПАРАЛЛЕЛЬНОЕ и ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЯ КОНДЕНСАТОРОВ. Параллельное соединение конденсаторов (рис. 144). У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна jA – jB. Если емкости отдельных конденсаторов С 1, С 2 ,..., Сn, то, их заряды равны Последовательное соединение конденсаторов (рис. 145). У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.60.62 (0.007 с.) |

 совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо l, называется электрическим моментом диполя или дипольным моментом.
совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо l, называется электрическим моментом диполя или дипольным моментом.

 Некомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными. Так как их поверхностная плотность s' меньше плотности s свободных зарядов плоскостей, то не все поле Е компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть — обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика Е = Е 0. Поверхностная плотность связанных зарядов s' равна поляризованности Р. Получим
Некомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными. Так как их поверхностная плотность s' меньше плотности s свободных зарядов плоскостей, то не все поле Е компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть — обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика Е = Е 0. Поверхностная плотность связанных зарядов s' равна поляризованности Р. Получим  откуда напряженность результирующего поля внутри диэлектрика равна
откуда напряженность результирующего поля внутри диэлектрика равна 
 называетсядиэлектрической проницаемостью среды.
называетсядиэлектрической проницаемостью среды. т. е. поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.
т. е. поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред. Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Е в самом общем виде можно записать как
Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Е в самом общем виде можно записать как  где
где  — соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S. Однако эта формула неприемлема для описания поля Е в диэлектрике, так как она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения.
— соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S. Однако эта формула неприемлема для описания поля Е в диэлектрике, так как она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения. откуда
откуда  (знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы). Поэтому
(знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы). Поэтому  и
и  (90.3) Заменив, согласно
(90.3) Заменив, согласно  , проекции вектора D проекциями вектора Е, умноженными на e0e, получим
, проекции вектора D проекциями вектора Е, умноженными на e0e, получим  (90.4) Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е (Еt) и нормальная составляющая вектора D (Dn) изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора Е (En) и тангенциальная составляющая вектора D (Dt) претерпевают скачок. Учитывая записанные выше условия, получим закон преломления линий напряженности Е (а значит, и линий смещения D)
(90.4) Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е (Еt) и нормальная составляющая вектора D (Dn) изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора Е (En) и тангенциальная составляющая вектора D (Dt) претерпевают скачок. Учитывая записанные выше условия, получим закон преломления линий напряженности Е (а значит, и линий смещения D) 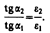 Эта формула показывает, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали.
Эта формула показывает, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали. Величину
Величину  (93.1) называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу. Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала. Получим, что емкость шара
(93.1) называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу. Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала. Получим, что емкость шара 
 (94.1) Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Получим выражение для емкости плоского конденсатора:
(94.1) Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Получим выражение для емкости плоского конденсатора:  , где e — диэлектрическая проницаемость. Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами r 1 и r 2 (r 2 > r 1), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Получим выражение для емкости цилиндрического конденсатора:
, где e — диэлектрическая проницаемость. Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами r 1 и r 2 (r 2 > r 1), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Получим выражение для емкости цилиндрического конденсатора:  Для определения емкости сферического конденсатора, состоящего из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r 1 и r 2 (r 2 > r 1) от центра заряженной сферической поверхности. Получим
Для определения емкости сферического конденсатора, состоящего из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r 1 и r 2 (r 2 > r 1) от центра заряженной сферической поверхности. Получим 
 а заряд батареи конденсаторов
а заряд батареи конденсаторов 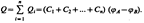 Полная емкость батареи
Полная емкость батареи  т. е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.
т. е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.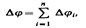 где для любого из рассматриваемых конденсаторов D ji = Q / Сi. С другой стороны,
где для любого из рассматриваемых конденсаторов D ji = Q / Сi. С другой стороны,  откуда
откуда  т. е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при.последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.
т. е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при.последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.


