Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность магнитного поля в среде. Проницаемость.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Напряжённость магнитного поля, векторная физическая величина (Н), являющаяся количественной характеристикой магнитного поля. Н. м. п. не зависит от магнитных свойств среды. В вакууме Н. м. п. совпадает с магнитной индукцией В; численно Н = В в СГС системе единиц и Н = В/m0 в Международной системе единиц (СИ), m0 — магнитная постоянная. В среде Н. м. п. Н определяет тот вклад в магнитную индукцию В, который дают внешние источники поля: Н = В — 4pj (в системе единиц СГС), или Н = (B/m0) — j (в СИ), где j — намагниченность среды. Магнитная проницаемость — физическая величина, характеризующая связь между магнитной индукцией B и магнитным полем H в веществе. Обозначается μ. У изотропных веществ μ = B / H (в Международной системе единиц СИ). Выделяют относительную и абсолютную магнитные проницаемости Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В) является обобщением закона (118.1):
ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ.
Вихревое электрическое поле не является фундаментальным физическим полем. Его природа состоит в действии обычных сил инерции, связанных с изменением скорости движения или скорости вращения полевой среды. Индукционное электрическое поле является вихревым. Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля. ПЛОТНОСТЬ ТОКА СМЕЩЕНИЯ. УРАВНЕНИЯ МАКСВЕЛЛА. Ток смещения — понятие из области теории классической электродинамики. Введено Дж. К. Максвеллом при построении теории электромагнитного поля для описания слабых токов, возникающих при смещении заряженных частиц в диэлектриках. Для описания и объяснения «прохождения» переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения. Итак, полная система уравнений Максвелла в интегральной форме: Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.199 (0.007 с.) |

 , где μr - относительная, а μ - абсолютная проницаемость, μ0 — магнитная постоянная.
, где μr - относительная, а μ - абсолютная проницаемость, μ0 — магнитная постоянная. где I и I' — соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L. Таким образом, циркуляция вектора магнитной индукции В по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Тогда закон полного тока для магнитного поля в веществе можно записать также в виде
где I и I' — соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L. Таким образом, циркуляция вектора магнитной индукции В по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Тогда закон полного тока для магнитного поля в веществе можно записать также в виде  (133.9) где I, подчеркнем это еще раз, есть алгебраическая сумма токов проводимости. Выражение, стоящее в скобках в (133.9), согласно (133.5), есть не что иное, как введенный ранее вектор H напряженности магнитного поля. Итак, циркуляция вектора Н по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром:
(133.9) где I, подчеркнем это еще раз, есть алгебраическая сумма токов проводимости. Выражение, стоящее в скобках в (133.9), согласно (133.5), есть не что иное, как введенный ранее вектор H напряженности магнитного поля. Итак, циркуляция вектора Н по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром:  (133.10) Выражение (133.10) представляет собой теорему о циркуляции вектора Н.
(133.10) Выражение (133.10) представляет собой теорему о циркуляции вектора Н.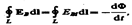 (137.1)
(137.1) 
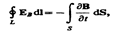 где символ частной производной подчеркивает тот факт, что интеграл
где символ частной производной подчеркивает тот факт, что интеграл  B d S является функцией только от времени. Циркуляция вектора напряженности электростатического поля (обозначим его E Q) вдоль любого замкнутого контура равна нулю:
B d S является функцией только от времени. Циркуляция вектора напряженности электростатического поля (обозначим его E Q) вдоль любого замкнутого контура равна нулю: (137.3) Сравнивая выражения (137.1) и (137.3), видим, что между рассматриваемыми полями (E B и Е Q) имеется принципиальное различие: циркуляция вектора E B в отличие от циркуляции вектора E Q не равна нулю. Следовательно, электрическое поле E B, возбуждаемое магнитным полем, как и само магнитное поле (см. § 118), является вихревым.
(137.3) Сравнивая выражения (137.1) и (137.3), видим, что между рассматриваемыми полями (E B и Е Q) имеется принципиальное различие: циркуляция вектора E B в отличие от циркуляции вектора E Q не равна нулю. Следовательно, электрическое поле E B, возбуждаемое магнитным полем, как и само магнитное поле (см. § 118), является вихревым.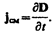 (138.2) Выражение (138.2) и было названо Максвеллом плотностью тока смещения.
(138.2) Выражение (138.2) и было названо Максвеллом плотностью тока смещения.
 где e 0 и m 0 — соответственно электрическая и магнитная постоянные, e и m — соответственно диэлектрическая и магнитная проницаемости, g — удельная проводимость вещества. Можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):
где e 0 и m 0 — соответственно электрическая и магнитная постоянные, e и m — соответственно диэлектрическая и магнитная проницаемости, g — удельная проводимость вещества. Можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):