
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силовые линии магнитного поляСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Магнитное поле, как и электростатическое, удобно представлять в графической форме – с помощью силовых линий магнитного поля.
Силовые линии магнитного поля проводят так, что их густота пропорциональна величине магнитной индукции: чем больше магнитная индукция в некоторой точке, тем больше густота силовых линий. Таким образом, силовые линии магнитного поля имеют сходство с силовыми линиями электростатического поля. Однако им свойственны и некоторые особенности. Рассмотрим магнитное поле, созданное прямым проводником с током I. Пусть этот проводник перпендикулярен плоскости рисунка. В различных точках, расположенных на одинаковых расстояниях от проводника, индукция одинакова по величине. Направление вектора В в разных точках показано на рисунке. Линией, касательная к которой во всех точках совпадает с направлением вектора магнитной индукции, является окружность.
Таким образом, силовые линии магнитного поля замкнуты (силовые линии электростатического не могут быть замкнуты, они начинаются и заканчиваются на зарядах). Поэтому магнитное поле является вихревым (так называют поля, силовые линии которых замкнуты).
Поэтому не бывает отдельно существующе-го северного или южного магнитного полюса магнита. Даже если распилить пополам постоянный магнит, то получится два магнита, каждый из которых имеет оба полюса. Сила Лоренца
Экспериментально установлено, что на заряд, движущийся в магнитном поле, действует сила. Эту силу принято называть силой Лоренца:
Модуль силы Лоренца
где a – угол между векторами v и B. Направление силы Лоренца зависит от направления вектора Дело в том, что сила Лоренца равна результату произведения вектора [ v, В ] на скаляр q. Если заряд положительный, то F л параллельна вектору [ v, В ]. Если же q < 0, то сила Лоренца противоположна направлению вектора [ v, В ] (см. рисунок). Если заряженная частица движется параллельно силовым линиям магнитного поля, то угол a между векторами скорости и магнитной индукции равен нулю. Следовательно, сила Лоренца на такой заряд не действует (sin 0 = 0, Fл = 0). Если же заряд будет двигаться перпендикулярно силовым линиям магнитного поля, то угол a между векторами скорости и магнитной индукции равен 900. В этом случае сила Лоренца имеет максимально возможное значение: Fл = q v B. Сила Лоренца всегда перпендикулярна скорости движения заряда. Это означает, что сила Лоренца не может изменить величину скорости движения, но изменяет её направление. Поэтому в однородном магнитном поле заряд, влетевший в магнитное поле перпендикулярно его силовым линиям, будет двигаться по окружности. Если на заряд действует только сила Лоренца, то движение заряда подчиняется следующему уравнению, составленному на основе второго закона Ньютона: ma = Fл. Поскольку сила Лоренца перпендикулярна скорости, постольку ускорение заряженной частицы является центростремительным (нормальным): Используя выражение для расчёта ускорения и заменив Fл на q v B, получаем
Отсюда следует, что радиус окружности, по которой будет двигаться заряд в однородном магнитном поле, равен
Если заряженная частица влетит в однородное магнитное поле под углом a к силовым линиям, то её траектория будет более сложной. Для того чтобы установить форму траектории и её параметры, разложим скорость частицы на две компоненты – параллельную v || = vcosa и перпендикулярную v ^= v sina силовым линиям магнитного поля. Компонента скорости v|| не изменяется, так как сила Лоренца не действует на заряженную частицу, движущуюся параллельно силовым линиям магнитного поля. За счёт этой компоненты заряд будет равномерно двигаться вдоль силовых линий.
Заряженная частица одновременно будет участвовать в этих движениях, поэтому её траектория будет представлять собой винтовую линию. Радиус винтовой линии будет равен Период обращения заряженной частицы равен времени, за которое она пройдёт один виток, Шаг винтовой линии равен расстоянию, которое заряд пройдёт за один период: L = v || T. Рассмотрим два одноимённых заряда, движущихся с одинаковой скоростью v вдоль параллельных прямых. За счёт кулоновского взаимодействия они отталкиваются с силой Каждый из зарядов создаёт магнитное поле. Следовательно, на заряды действует сила Лоренца. Заряд q 1 создаёт магнитное поле, индукция которого направлена на нас (см. рисунок), и по модулю равна
Тогда сила Лоренца, действующая на второй заряд, по модулю равна
и направлена так, как показано на рисунке справа. Отношение силы Лоренца к кулоновской силе равно
Значения величин eо и mо связаны между собой соотношением
Таким образом, в рассматриваемой ситуации сила Лоренца меньше кулоновской и возрастает по мере роста скорости движения заряда. Это ещё раз указывает на релятивистский характер магнитного взаимодействия.
Сила Ампера
Если проводник с током поместить в магнитное поле, то на каждый электрон, направленно движущийся в проводнике, действует сила Лоренца. Действие этой силы передаётся всему проводнику. В результате на проводник с током, находящийся в магнитном поле, будет действовать некоторая сила. Найдём её величину. Для этого выделим элементарный участок проводника d l. Результирующая сила d F, действующая на элемент проводника, равна сумме сил, действующих на все электроны в участке d l:
поскольку q. n. v = j, постольку сила d F равна
Это и есть выражение для расчёта силы Ампера, т. е. силы, действующей на элемент проводника с током, находящийся в магнитном поле. Направление силы Ампера совпадает с направлением вектора Для вычисления силы, действующей на весь проводник, необходимо взять интеграл от d F по длине проводника:
Теперь рассмотрим два параллельных проводника с токами I 1 и I 2, расположенных на расстоянии b друг от друга. Первый проводник создаёт магнитное поле, индукция которого
В этом поле на единицу длины второго проводника действует сила, равная
Такая же по величине сила действует и на первый проводник. Легко увидеть, что если токи направлены в одну сторону, проводники притягиваются, если же токи противоположны, то проводники отталкиваются.
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1783; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.114 (0.007 с.) |

 Силовая линия магнитного поля – это линия, касательная к которой в каждой точке совпадает с направлением вектора магнитной индукции.
Силовая линия магнитного поля – это линия, касательная к которой в каждой точке совпадает с направлением вектора магнитной индукции. Следовательно, силовые линии магнитного поля в этом случае представляют собой окружности, охватывающие проводник. Центры всех силовых линий расположены на проводнике.
Следовательно, силовые линии магнитного поля в этом случае представляют собой окружности, охватывающие проводник. Центры всех силовых линий расположены на проводнике. Замкнутость силовых линий означает ещё одну, очень важную особенность магнитного поля – в природе не существует (по крайней мере, пока не обнаружено) магнитных зарядов, которые являлись бы источником магнитного поля определённой полярности.
Замкнутость силовых линий означает ещё одну, очень важную особенность магнитного поля – в природе не существует (по крайней мере, пока не обнаружено) магнитных зарядов, которые являлись бы источником магнитного поля определённой полярности. .
.
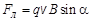 ,
, . Его можно определить с помощью правила правого винта или правила левой руки. Но направление силы Лоренца не обязательно совпадает с направлением вектора
. Его можно определить с помощью правила правого винта или правила левой руки. Но направление силы Лоренца не обязательно совпадает с направлением вектора 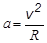 (здесь R – радиус кривизны траектории заряженной частицы).
(здесь R – радиус кривизны траектории заряженной частицы). .
. .
. Компонента скорости v ^ не будет меняться по величине, но будет непрерывно изменяться её направление. За счёт этой компоненты заряд будет двигаться по окружности, плоскость ко-торой перпендикулярна силовым линиям.
Компонента скорости v ^ не будет меняться по величине, но будет непрерывно изменяться её направление. За счёт этой компоненты заряд будет двигаться по окружности, плоскость ко-торой перпендикулярна силовым линиям.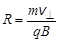 .
. .
. .
. .
.


 .
. , где с – скорость света в вакууме. Поэтому
, где с – скорость света в вакууме. Поэтому .
. .
. ;
; .
. и может быть определено по правилу правого винта для векторного произведения (или по правилу левой руки).
и может быть определено по правилу правого винта для векторного произведения (или по правилу левой руки).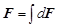 .
. .
.
 .
.


