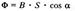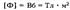Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитный поток. Теорема Гаусса для магнитного поля в вакууме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Внешняя часть магнитного поля(определяемая числом магнитных силовых линий), направленных от северного полюса магнита,называется магнитным потоком. Магнитный поток численно выражается общим количеством магнитных силовых линий,проходящих через определённую площадь и обозначаются Ф. Потоком вектора магнитной индукции или магнитным потоком сквозь малую поверхность площадью dS называется скалярная физическая величина, равная
Ф =
Отсюда определяется единица магнитного потока вебер (Вб): 1 Вб – это магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл, т.е. 1 Вб = 1 Тл·м2. Теорема Гаусса для магнитного поля формулируется следующим образом: поток вектора магнитной индукции сквозь произвольную замкнутую поверхность равен нулю: Эта теорема отражает тот факт, что в природе не существует магнитных масс (магнитных зарядов) – источников магнитного поля, на которых начинались бы или заканчивались линии магнитной индукции. Вследствие этого силовые линии магнитного поля не имеют ни начала, ни конца и являются замкнутыми. Циркуляция вектора магнитной индукции. Закон полного тока. Циркуляция вектора В по заданному замкнутому контуру называется интеграл
30. Поток магнитной индукции. Правило Ленца. Магнитный поток пропрционален числу линий магнитной индукции, пронизывающих поверхность площадью S.
Магнитный поток характеризует распределение магнитного поля по поверхности, ограниченной контуром. Магнитный поток в 1Вб создается однородным магнитным полем с индукцией 1Тл через поверхность площадью 1м2, расположенной перпендикулярно вектору магнитной индукции. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА Прямолинейный проводник Направление индукционного тока определяется по правилу правой руки:Если поставить правую руку так, чтобы вектор магнитной индукции входил в ладонь, отставленный на 90 градусов большой палец указывал направление вектора скорости, то выпрямленные 4 пальца покажут направление индукционного тока в проводнике. Замкнутый контур Направление индукционного тока в замкнутом контуре определяется по правилу Ленца. Правило Ленца:
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.145.219 (0.006 с.) |

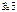 ), где
), где 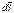 - число линий, пронизывающих площадь,
- число линий, пронизывающих площадь, 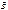 - поле.
- поле. Магнитный поток сквозь произвольную поверхность площадью S равен
Магнитный поток сквозь произвольную поверхность площадью S равен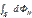 =
= 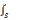 (
(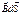 )
)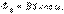
 Если плоская поверхность расположена перпендикулярно вектору
Если плоская поверхность расположена перпендикулярно вектору 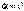 и
и 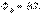
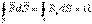
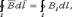 , где dl – вектор элементарной длины контура, направленный вдоль обхода контура, В1=Вcosα – составляющая вектора В в направлении касательной к контуру, α – угол между векторами В и dl. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых этим контуром:
, где dl – вектор элементарной длины контура, направленный вдоль обхода контура, В1=Вcosα – составляющая вектора В в направлении касательной к контуру, α – угол между векторами В и dl. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых этим контуром: 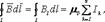 где n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов,
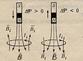
где n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов, 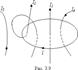 - ΣIk=I1+2I2-0*I3-I4. Выражение справедливо только для поля в вакууме, поскольку для поля в веществе необходимо учитывать молекулярные токи.
- ΣIk=I1+2I2-0*I3-I4. Выражение справедливо только для поля в вакууме, поскольку для поля в веществе необходимо учитывать молекулярные токи.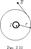 Магнитное поле прямого тока I перпендикулярно плоскости чертежа направленно к нам. Замкнутый контур в виде окружности радиуса r. В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора В равна
Магнитное поле прямого тока I перпендикулярно плоскости чертежа направленно к нам. Замкнутый контур в виде окружности радиуса r. В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора В равна 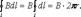 Получаем В*2πr=μ0*I (в вакууме), откуда
Получаем В*2πr=μ0*I (в вакууме), откуда 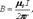 . Таким образом, исходя из теоремы о циркуляции вектора В получили выражение для магнитной индукции поля прямого тока.
. Таким образом, исходя из теоремы о циркуляции вектора В получили выражение для магнитной индукции поля прямого тока.