
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Гауса для поля в диэлектрике.Содержание книги
Поиск на нашем сайте
Если диэлектрик выбрать в форме прямоугольного параллелепипеда, то Для большого класса диэлектриков поляризованность пропорциональна напряженности поля в диэлектрике:
Таким образом, Если поляризация однородна, то внутри диэлектрика. Поле внутри диэлектрика обусловлено как свободными, так и связанными зарядами и. теорему Гаусса для вектора Е можно записать: Подставим в данное выражение Следовательно, Введем новый вектор вектор электрического смещения. Тогда - это и есть теорема Гаусса для электростатического поля в диэлектрике. Из формулы (13) видно, что поток вектора D через замкнутую поверхность определяется только свободными зарядами. Формулировка теоремы Гаусса для поля D: поток вектора электрического смещения через произвольную замкнутую поверхность равен сумме свободных зарядов, охватываемых этой поверхностью.
14. Энергия и плотность энергии электрического поля. Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие. Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Следует отметить, что, строго говоря, термин энергия электромагнитного поля является не вполне корректным. Вычисление полной энергии электрического поля даже одного электрона приводит к значению равному бесконечности, поскольку соответствующий интеграл (см. ниже) расходится. Бесконечная энергия поля вполне конечного электрона составляет одну из теоретических проблем классической электродинамики. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определенной точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству. Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей. В системе СИ: В вакууме (а также в веществе при рассмотрении микрополей):
где E — напряжённость электрического поля, B — магнитная индукция, D — электрическая индукция, H — напряжённость магнитного поля, с — скорость света, — электрическая постоянная, и — магнитная постоянная. Иногда для констант и — используют термины диэлектрическая проницаемость и магнитная проницаемость вакуума, — которые являются крайне неудачными, и сейчас почти не употребляются.
Магнитное поле в вакууме. Силовые линии магнитного поля Магнитное поле — это особый вид материи, посредством которой осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом. Свойства: Индуктивность, Напряженность Приращение плотности энергии магнитного поля равно: Dw= H*dB где: H — напряжённость магнитного поля, B— магнитная индукция Силовые линии магнитного поля
Индукция магнитного поля. Магнитная индукция «B» — векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Показывает, с какой силой «F» магнитное поле действует на заряд «q», движущийся со скоростью «v» Магнитную индукцию можно определить с помощью рамки с током, через силу Ампера, через силу Лоренца. Сила Лоренца — сила, с которой магнитное поле действует на точечную заряженную частицу. F= q*v*B*sin(B^v) Где q – заряд частицы v-скорость движущейся частицы B-магнитная индукция
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.94.189 (0.007 с.) |

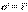 (8)
(8) (9)где X - диэлектрическая восприимчивость вещества. Подставим (9) в (8), а затем получивщееся выражение в (3):
(9)где X - диэлектрическая восприимчивость вещества. Подставим (9) в (8), а затем получивщееся выражение в (3):
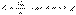 - диэлектрическая проницаемость среды, показывает во сколько раз поле внутри диэлектрика меньше поля в вакууме. Как видно из формулы, напряженность электростатического поля зависит от свойств среды. При неоднородной поляризации связанные заряды могут появиться не только на поверхности, но и в объеме диэлектрика. Вычислим заряд, появляющийся внутри диэлектрика при неоднородной поляризации. Выделим мысленно в диэлектрике произвольный объем V, ограниченный замкнутой поверхностью S. Заряд, смещенный при поляризации через площадку dS в отрицательном направлении нормали равен. Через всю поверхность S внутрь объема V при поляризации поступает поляризационный заряд:
- диэлектрическая проницаемость среды, показывает во сколько раз поле внутри диэлектрика меньше поля в вакууме. Как видно из формулы, напряженность электростатического поля зависит от свойств среды. При неоднородной поляризации связанные заряды могут появиться не только на поверхности, но и в объеме диэлектрика. Вычислим заряд, появляющийся внутри диэлектрика при неоднородной поляризации. Выделим мысленно в диэлектрике произвольный объем V, ограниченный замкнутой поверхностью S. Заряд, смещенный при поляризации через площадку dS в отрицательном направлении нормали равен. Через всю поверхность S внутрь объема V при поляризации поступает поляризационный заряд:  (10)
(10) (11)
(11)

 (12)
(12) (13)
(13)





