
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрический заряд. Взаимодействие электрических зарядов. Закон Кулона. Принцип суперпозиции для сил.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электрический заряд. Взаимодействие электрических зарядов. Закон Кулона. Принцип суперпозиции для сил. Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Электрический заряд обычно обозначается буквами q или Q. Существует два рода электрических зарядов, условно названных положительными и отрицательными. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд. Одноименные заряды отталкиваются, разноименные – притягиваются. Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов, отличавшихся чрезвычайно высокой чувствительностью. Идея измерений основывалась на том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами (заряженное тело, размерами которого в условиях данной задачи можно пренебречь.)
Силы взаимодействия подчиняются третьему закону Ньютона. Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках. Взаимодействие.неподвижных.электрических.зарядов.называют электростатическим или кулоновским взаимодействием.
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции. Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел. Если к системе из двух заряженных шаров поднсти третий заряженный шар, то взаимодействие между 1 и 2 изменится из-за перераспределения зарядов. Принцип суперпозиции утверждает, что при заданном (фиксированном) распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.
Если в данной точке пространства различные заряды создают электрические поля направление который Е1,Е2 ит.д. то результирующая напряжённость поля в этой точке равна геометрической сумме полей Е1,Е2 и т.д.
Условие стационарности тока Окружим участок проводника, по которому течет ток с плотностью
или
16. Закон Ома для участка цепи. Электрическое сопротивление. Закон Ома в дифференциальной форме. Закон Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома.
И записывается формулой: Где: I — сила тока (А), U — напряжение (В), R — сопротивление (Ом). Следует иметь в виду, что закон Ома является фундаментальным (основным) и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов. Закон Ома в дифференциальной форме Сопротивление Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно определить как R — сопротивление; U — разность электрических потенциалов на концах проводника, измеряется в вольтах; I — ток, протекающий между концами проводника под действием разности потенциалов, измеряется в амперах. Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он состоит. Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле: где ρ — удельное сопротивление вещества проводника, L — длина проводника, а S — площадь сечения. Удельное сопротивление — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади. Прямолинейный проводник Направление индукционного тока определяется по правилу правой руки:Если поставить правую руку так, чтобы вектор магнитной индукции входил в ладонь, отставленный на 90 градусов большой палец указывал направление вектора скорости, то выпрямленные 4 пальца покажут направление индукционного тока в проводнике. Замкнутый контур Направление индукционного тока в замкнутом контуре определяется по правилу Ленца. Правило Ленца:
Правило Ленца Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока,которым он связан.Это правило позволяет определить направление индукционного тока. Применение правила Ленца: 1.установить направление линий магнитной индукции внешнего магнитного поля. 2.выяснить,увеличивается или уменьшается поток магнитной индукции этого поля через поверхность,ограниченную этим контуром. 3.установить направление линий магнитной индукции магнитного поля индукционного тока. Эти линии, согласно правилу Ленца, должны быть направлены противоположно линиям магнитной индукции внешнего поля при увеличении магнитного потока и иметь одинаковое с ними направление при уменьшении магнитного потока. 4.зная направление линий магнитной индукции, можно найти направление индукционного тока,пользуясь правилом буравчика.
Энергия магнитного поля. Для определения энергии магнитного поля рассмотрим контур, состоящий из источника э.д.с. - ε, катушки индуктивности - L и сопротивления - R (рис.3.4). При замыкании цепи ток возрастает от 0 до I, и, следовательно, возникает э.д.с. самоиндукции εis, направленная против э.д.с. ε, возбуждающей ток. При размыкании цепи сила тока уменьшается от I до 0, что вызывает появление э.д.с. самоиндукции εis того же направления, что и направление внешней ε. Можно предположить, что на увеличение тока в контуре затрачивается дополнительная работа, идущая на создание энергии магнитного поля. При снижении тока эта энергия выделяется в виде дополнительного джоуль-ленцева тепла.
Подсчитаем работу, совершаемую источником э.д.с. за время dt. Для этого воспользуемся формулой для мощности тока N=dA/dt=Iε. Объединив два последних выражения, получим
Первое слагаемое dA1 = I2Rdt – это работа, расходуемая на нагревание проводника, т.е. тепло, выделяемое в проводнике за время dt. Второе слагаемое dA2 = LIdI – работа, обусловленная индукционными явлениями. Данная дополнительная работа, затрачиваемая на увеличение силы тока в контуре от 0 до I, находится как интеграл:
Увеличение силы тока в проводнике вызывает соответствующее усиление его магнитного поля, которое, подобно электрическому, обладает энергией. Найденная нами собственная энергия тока в контуре есть не что иное, как энергия Wm магнитного поля этого контура с током. Эта энергия запасена в магнитном поле катушки так же, как энергия электрического поля запасена в заряженном конденсаторе. Таким образом, L = n2μμ0V. Индукция магнтного поля соленоида В = nμμ0I, откуда I=B/nμμ0. Таким образом, искомая энергия:
Так как В= μμ0Н, то Если магнитное поле однородно, его энергия распределена равномерно по всему объему поля с некоторой объемной плотностью wm: Последнее соотношение можно переписать в трех эквивалентных формах: .Если магнитное поле неоднородно, его объемная плотность меняется от точки к точке. Зная wm в каждой точке, можно найти энергию поля, заключенную в некотором объеме V. Для этого нужно вычислить интеграл:
Электромагнитные волны Английский ученый Джеймс Максвелл высказал гипотезу о существовании в природе особых волн, способных распространяться в вакууме. Эти волны Максвелл назвал электромагнитными волнами. По представлениям Максвелла: при любом изменении электрического поля возникает вихревое магнитное поле и, наоборот, при любом изменении магнитного поля возникает вихревое электрическое поле. Процесс взаимопорождения электрических и магнитных полей происходит во взаимно перпендикулярных плоскостях. Переменное электрическое поле порождает вихревое магнитное поле, переменное магнитное поле порождает вихревое электрическое поле. Электрические и магнитные поля могут существовать не только в веществе, но и в вакууме. Поэтому должно быть возможным распространение электромагнитных волн в вакууме. Условием возникновения электромагнитных волн является ускоренное движение электрических зарядов. Так, изменение магнитного поля происходит при изменении тока в проводнике, а изменение тока происходит при изменении скорости зарядов, т. е. при движении их с ускорением. Скорость распространения электромагнитных волн в вакууме, по расчетам Максвелла, должна быть приблизительно равна 300 000 км/с. Впервые опытным путем получил электромагнитные волны физик Генрих Герц, использовав при этом высокочастотный искровой разрядник (вибратор Герца). Герц опытным путем определил также скорость электромагнитных волн. Она совпала с теоретическим определением скорости волн Максвеллом. Простейшие электромагнитные волны — это волны, в которых электрическое и магнитное поля совершают синхронные гармонические колебания. Электромагнитные волны обладают всеми основными свойствами волн. Они подчиняются закону отражения волн: угол падения равен углу отражения. При переходе из одной среды в другую преломляются и подчиняются закону преломления волн: отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух данных сред и равная отношению скорости электромагнитных волн в первой среде к скорости электромагнитных волн во второй среде и называется показателем преломления второй среды относительно первой. Явление дифракции электромагнитных волн, т. е. отклонение направления их распространения от прямолинейного, наблюдается у края преграды или при прохождении через отверстие. Электромагнитные волны способны к интерференции. Интерференция — это способность когерентных волн к наложению, в результате чего волны в одних местах друг друга усиливают, а в других местах — гасят. (Когерентные волны — это волны, одинаковые по частоте и фазе колебания.) Электромагнитные волны обладают дисперсией, т. е. когда показатель преломления среды для электромагнитных волн зависит от их частоты. Опыты с пропусканием электромагнитных волн через систему из двух решеток показывают, что эти волны являются поперечными. При распространении электромагнитной волны векторы напряженности Е и магнитной индукции В перпендикулярны направлению распространения волны и взаимно перпендикулярны между собой. Если электромагнитные волны возникают в контуре из катушки и конденсатора, то переменное магнитное поле оказывается связанным с катушкой, а переменное электрическое поле — сосредоточенным между пластинами конденсатора. Такой контур называется закрытым. Закрытый колебательный контур практически не излучает электромагнитные волны в окружающее пространство. Если контур состоит из катушки и двух пластин плоского конденсатора, то под чем большим углом развернуты эти пластины, тем более свободно выходит электромагнитное поле в окружающее пространство Предельным случаем раскрытого колебательного контура является удаление пластин на противоположные концы катушки. Такая система называется открытым колебательным контуром.
Шкала электромагнитных волн Электромагнитные волны пронизывают все окружающее нас пространство. В первую очередь это свет, а также радиоволны, тепловое излучение, ультра-фиолетовое, рентгеновское и γ-излучение. Все эти электромагнитные волны различаются по длине волны и, соответственно, по частоте. Длины электромагнитных волн лежат в пределе V=лямда на ню Лямда = от 108до1013 Общим для всех электромагнитных излучений являются механизмы их возникновения: электромагнитные волны с любой длиной волны могут возникать при ускоренном движении электрических зарядов или при переходах молекул, атомов или атомных ядер из одного квантового состояния в другое. Гармонические колебания электрических зарядов сопровождаются электромагнитным излучением, имеющим частоту, равную частоте колебаний зарядов.
Интерференция на клине.
Рассмотрим интерференционную картину, получаемую от пластинок переменной толщины (от клина). Направления распространения световой волны, отраженной от верхней и нижней границы клина, не совпадают. Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость). Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности. Результат интерференции в точках
Закон Малюса. До сих пор при исследовании дифракции или интерференции мы занимались волнами без учета их поляризации. Можно сказать, что в случае волн поперечных, мы считали их поляризованными одинаково. Только в этом случае с помощью векторной диаграммы можно складывать амплитуды колебаний, т.е. в случае, если они происходят по одному направлению. Теперь нам нужно сосредоточиться на поперечных волнах, при сложении которых может оказаться существенной поляризация волны. Поляризация определяется тем, как направлен, например, вектор электрического поля в плоскости, перпендикулярной к направлению распространения волны. Вектор В естественном свете это направление изменяется случайным образом. Такой свет называют неполяризованным.
o
фотоприемник Каким образом можно судить о поляризованности света? Имеются приборы, которые пропускают только свет с определенным направлением вектора Кроме света неполяризованного выделяют частично поляризованный свет. В этом случае направление вектора электрического поля также изменяется хаотически, но имеется некоторое направление, при котором в среднем амплитуда колебаний больше. Для такого случая вводится понятие степени поляризации: вращая анализатор, определяют значения максимальной и минимальной интенсивности, воспринимаемой фотоприемником. Степень поляризации определяется выражением: Частично поляризованным может быть смесь неполяризованного и линейно поляризованного света.
E0 O’
Eôê E^ j
O Для линейно поляризованного света справедлив закон Малюса. Пусть колебания электрического вектора происходят в вертикальной плоскости и амплитуда колебаний равна E0. Если ось анализатора повернута не угол j по отношению к направлению поляризации, к фотоприемнику пройдет свет с амплитудой Поскольку интенсивность света пропорциональна квадрату амплитуды, мы получаем закон Малюса
Опыт Боте. Фотоны. Эйнштейн выдвинул гипотезу, что свет распространяется в виде дискретных частиц, названных первоначально световыми квантами. Впоследствии эти частицы получили название фотоны. Таким образом, фотоны - световые кванты. Наиболее непосредственное подтверждение гипотезы Эйнштейна дал опыт Боте. Тонкая металлическая фольга помещалась между двумя газозярядными счетчиками. Фольга освещалась слабым пучком рентгеновских лучей, под действием которых она сама начинала испускать рентгеновские кванты, которые фиксировались счетчиками. При попадании в него рентгеновских лучей счетчик срабатывал и приводил в действие особый механизм М, делавший отметку на движущейся ленте Л. Если бы излучаемая энергия распространялась равномерно во все стороны, оба счетчика должны были срабатывать одновременно и отметке на ленте приходились бы одна против другой. В действительности же наблюдалось совершенно беспорядочное расположение отметок. Это можно объяснить лишь тем, что в отдельных актах излучения возникают световые частицы - фотоны, летящие то в одном, то в другом направлении.
Это и доказывает существование особых световых частиц – фотонов. Фотон, подобно всем частицам обладает определенной порцией энергии E=hn. Энергию фотона часто выражают не через частоту n, а через циклическую частоту w=2pn, при этом в качестве коэффициент пропорциональности вместо величины h используют величину Найдем импульс фотона: Из квантового соотношения E= масса фотона равна нулю, фотон всегда движется со скоростью света с Это означает, что фотон представляет собой частицу особого рода, отличную от таких частиц, как электрон, протон и т.п., которые могут существовать, двигаясь со скоростями,, меньшими с, и даже покоясь.
Масса и энергия связи ядра Масса и энергия связи ядра Масса ядра измеряется в атомных единицах массы (а.е.м). За одну атомную единицу массы принимается 1/12 часть массы нейтрального атома углерода 12 С: 1а.е.м = 1.6606 10-27 кг. А.е.м. выражается через энергетические единицы: 1а.е.м = 1.510-3 эрг = 1.510-10Дж = 931.49 МэВ Масса ядра всегда меньше суммы масс составляющих его нуклонов. Есв(A, Z) = [Z mp + (A - Z)mn - M(A, Z)]c2, где Z - число протонов, (A - Z) - число нейтронов, mp - масса протона, mn - масса нейтрона, М(A,Z) - масса ядра с массовым числом А и зарядом Z. Есв(A, Z) = [ZmH + (A - Z)mn - Mат(A, Z)]c2, где mH - масса атома водорода. Удельная энергия связи ядра ε(A, Z) это энергия связи, приходящаяся на один нуклон ε(A, Z) = Eсв(A,Z) / A. На рис. 1 показана зависимость удельной энергии связи ядра Избыток масс (дефект масс) Δ связан с массой атома Mат(A,Z) и массовым числом A соотношением: Δ = Мат(A,Z) - А.
Исследовательские реакторы Квантование энергии Формула Планка. Некоторые физические величины, относящиеся к микрообъектам, изменяются не непрерывно, а скачкообразно. О величинах, которые могут принимать только вполне определенные, то есть дискретные значения (латинское "дискретус" означает разделенный, прерывистый), говорят, что они квантуются. В 1900 г. немецкий физик М. Планк, изучавший тепловое излучение твердых тел, пришел к выводу, что электромагнитное излучение испускается в виде отдельных порций - квантов - энергии. Значение одного кванта энергии равно Δ E = h ν, где Δ E - энергия кванта, Дж; ν - частота, с-1; h - постоянная Планка (одна из фундаментальных постоянных природы), равная 6,626·10−34 Дж·с. Идея о квантовании энергии позволила объяснить происхождение линейчатых атомных спектров, состоящих из набора линий, объединенных в серии. В своих расчетах Планк выбрал наиболее простую модель излучающей системы (стенок полости) в виде гармонических осцилляторов (электрических диполей) со всевозможными собственными частотами. Здесь Планк следовал Рэлею. Но Планку пришла мысль связать с энергией осциллятора не его температуру, а его энтропию. Оказалось, что полученное выражение хорошо описывает экспериментальные данные (октябрь 1900 г.). Однако обосновать свою формулу Планк смог только в декабре 1900 года, после того, как более глубоко понял вероятностный смысл энтропии, на которую указал Больцман ( Термодинамическая вероятность В данном случае это число возможных способов распределения энергии между осцилляторами. Однако, такой процесс подсчета возможен, если энергия будет принимать не любые непрерывные значения, а лишь дискретные значения, кратные некоторой единичной энергии. Эта энергия колебательного движения должна быть пропорциональна частоте. Итак, энергия осциллятора должна быть целым кратным некоторой единицы энергии, пропорциональной его частоте.
Минимальная порция энергии Где Окончательный вид формулы Планка:
Атом водорода по Бору. Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модель атома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать непрерывно, и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка[1]:
Здесь me — масса электрона, Z — количество протонов в ядре, Именно такое выражение для энергии можно получить, применяя уравнение Шрёдингера, решая задачу о движении электрона в центральном кулоновском поле. Радиус первой орбиты в атоме водорода R0=5,2917720859(36)×10−11 м[2], ныне называется боровским радиусом, либо атомной единицей длины и широко используется в современной физике. Энергия первой орбиты E 0 = − 13.6 эВ представляет собой энергию ионизации атома водорода. Достоинства теории Бора 1) Объяснила дискретность энергетических состояний водородоподобных атомов. 2)Теория Бора подошла к объяснению внутриатомных процессов с принципиально новых позиций, стала первой полуквантовой теорией атома. 3)Эвристическое значение теории Бора состоит в смелом предположении о существовании стационарных состояний и скачкообразных переходов между ними. Эти положения позднее были распространены и на другие микросистемы. Недостатки теории Бора 1) Не смогла объяснить интенсивность спектральных линий. 2)Справедлива только для водородоподобных атомов и не работает для атомов, следующих за ним в таблице Менделеева. 3)Теория Бора логически противоречива: не является ни классической, ни квантовой. В системе двух уравнений, лежащих в её основе, одно — уравнение движения электрона — классическое, другое — уравнение квантования орбит — квантовое. Теория Бора являлась недостаточно последовательной и общей. Поэтому она в дальнейшем была заменена современной квантовой механикой, основанной на более общих и непротиворечивых исходных положениях. Сейчас известно, что постулаты Бора являются следствиями более общих квантовых законов. Но правила квантования типа широко используются и в наши дни как приближенные соотношения: их точность часто бывает очень высокой.
Индукция магнитного поля. Магнитная индукция «B» — векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Показывает, с какой силой «F» магнитное поле дейс
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.212.129 (0.02 с.) |

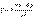
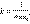
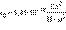 – электрическая постоянная.
В системе СИ элементарный заряд e равен:
e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.
– электрическая постоянная.
В системе СИ элементарный заряд e равен:
e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.
 , замкнутой поверхностью S. По определению вектора
, замкнутой поверхностью S. По определению вектора  не будет постоянным. Отсюда следует условие стационарности тока:
не будет постоянным. Отсюда следует условие стационарности тока: 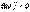
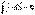 . Линии постоянного или стационарного тока нигде не должны начинаться или заканчиваться: они замкнуты. Поэтому цепь постоянного тока обязательно должна быть замкнута.
. Линии постоянного или стационарного тока нигде не должны начинаться или заканчиваться: они замкнуты. Поэтому цепь постоянного тока обязательно должна быть замкнута.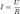
 зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.
зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.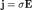 где:
где:  — вектор плотности тока,
— вектор плотности тока, — удельная проводимость,
— удельная проводимость,  — вектор напряжённости электрического поля. Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1). Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред. Электри́ческое сопротивле́ние — скалярная физическая величина, характеризующая свойства проводника и равная отношению напряжения на концах проводника к силе электрического тока, протекающему по нему.
— вектор напряжённости электрического поля. Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1). Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред. Электри́ческое сопротивле́ние — скалярная физическая величина, характеризующая свойства проводника и равная отношению напряжения на концах проводника к силе электрического тока, протекающему по нему.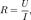 где
где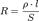
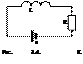 Пусть при замыкании контура ток меняется со скоростью dI/dt. Тогда, как мы уже знаем, в контуре индуцируется э.д.с. самоиндукции εs, равная -LdI/dt, препятствующая изменениям тока. В контуре действует также постоянная э.д.с. ε. Если за положительное направление тока принять то направление, в котором ε заставляет течь ток в контуре, то полная э.д.с. в любой момент времени будет равна ε- LdI/dt. Эта суммарная э.д.с. вызывает ток I через сопротивление R. На сопротивлении происходит падение напряжения, равное IR. Закон Ома для контура имеет вид
Пусть при замыкании контура ток меняется со скоростью dI/dt. Тогда, как мы уже знаем, в контуре индуцируется э.д.с. самоиндукции εs, равная -LdI/dt, препятствующая изменениям тока. В контуре действует также постоянная э.д.с. ε. Если за положительное направление тока принять то направление, в котором ε заставляет течь ток в контуре, то полная э.д.с. в любой момент времени будет равна ε- LdI/dt. Эта суммарная э.д.с. вызывает ток I через сопротивление R. На сопротивлении происходит падение напряжения, равное IR. Закон Ома для контура имеет вид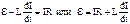 .
.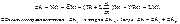
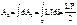 Полученная работа LI2/2 представляет собой собственную энергию тока в контуре с индуктивностью L.
Полученная работа LI2/2 представляет собой собственную энергию тока в контуре с индуктивностью L.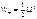 В этой формуле магнитная энергия выражена через параметры, характеризующие контур с током – силу тока I и индуктивность катушки L. Ту же энергию Wm можно выразить через параметры, характеризующие само магнитное поле, а именно, напряженность поля
В этой формуле магнитная энергия выражена через параметры, характеризующие контур с током – силу тока I и индуктивность катушки L. Ту же энергию Wm можно выразить через параметры, характеризующие само магнитное поле, а именно, напряженность поля 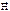 , магнитную индукцию
, магнитную индукцию 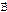 и объем занимаемого полем пространства V. Для этого найдем энергию магнитного поля соленоида. Воспользуемся полученным нами ранее выражением для индуктивности соленоида:
и объем занимаемого полем пространства V. Для этого найдем энергию магнитного поля соленоида. Воспользуемся полученным нами ранее выражением для индуктивности соленоида: .
.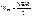 .
. .
.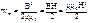
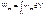

 и
и 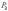 экрана определяется по известной формуле
экрана определяется по известной формуле  , подставляя в неё толщину пленки в месте падения луча (
, подставляя в неё толщину пленки в месте падения луча (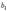 или
или 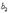 ). Свет обязательно должен быть параллельным (
). Свет обязательно должен быть параллельным ( ): если одновременно будут изменяться два параметра b и α, то устойчивой интерференционной картины не будет. Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рис. 8.11). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
): если одновременно будут изменяться два параметра b и α, то устойчивой интерференционной картины не будет. Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рис. 8.11). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.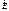 перпендикулярен направлению распространения волны, но это направление может тем или иным способом изменяться. Свет называют поляризованным, если наблюдается некоторая регулярность такого изменения.
перпендикулярен направлению распространения волны, но это направление может тем или иным способом изменяться. Свет называют поляризованным, если наблюдается некоторая регулярность такого изменения. анализатор
анализатор

 o’
o’
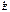 (в зависимости от назначения их называют поляризаторами или анализаторами). Если свет неполяризован, то при повороте анализатора вокруг горизонтальной оси интенсивность света, воспринимаемого фотоприемником, не изменяется: амплитуда колебаний электрического вектора остается неизменной.
(в зависимости от назначения их называют поляризаторами или анализаторами). Если свет неполяризован, то при повороте анализатора вокруг горизонтальной оси интенсивность света, воспринимаемого фотоприемником, не изменяется: амплитуда колебаний электрического вектора остается неизменной.
 Если неполяризованный свет проходит через поляризатор, он становится линейно или плоско поляризованным светом. В этом случае колебания вектора
Если неполяризованный свет проходит через поляризатор, он становится линейно или плоско поляризованным светом. В этом случае колебания вектора 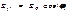
 . Свет с амплитудой E^ задерживается анализатором.
. Свет с амплитудой E^ задерживается анализатором.

 (аш с чертой), равную:
(аш с чертой), равную:  .Тогда энергия фотона записывается так: E=hn=
.Тогда энергия фотона записывается так: E=hn=  .
. . Импульс фотона направлен по световому лучу.
. Импульс фотона направлен по световому лучу.
 от числа нуклонов A. Видно, что наиболее сильно связаны ядра в районе железа и никеля (A ~ 55-60). Такой ход зависимости ε(A) показывает, что для легких ядер энергетически выгодны реакции синтеза более тяжелых ядер, а тяжелых - деление на более легкие осколки.
от числа нуклонов A. Видно, что наиболее сильно связаны ядра в районе железа и никеля (A ~ 55-60). Такой ход зависимости ε(A) показывает, что для легких ядер энергетически выгодны реакции синтеза более тяжелых ядер, а тяжелых - деление на более легкие осколки.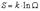 ).
). – число возможных микроскопических комбинаций, совместимое с данным состоянием в целом.
– число возможных микроскопических комбинаций, совместимое с данным состоянием в целом.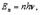 где n = 1, 2, 3…
где n = 1, 2, 3…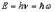
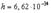 – постоянная Планка;
– постоянная Планка; 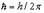 и
и 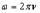 Принципиальное отличие вывода Планка от выводов Рэлея и других в том, что «не может быть и речи о равномерном распределении энергии между осцилляторами».
Принципиальное отличие вывода Планка от выводов Рэлея и других в том, что «не может быть и речи о равномерном распределении энергии между осцилляторами».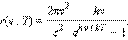
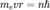 . Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты Rn и энергии En находящегося на этой орбите электрона:
. Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты Rn и энергии En находящегося на этой орбите электрона: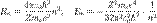
 — диэлектрическая постоянная, e — заряд электрона.
— диэлектрическая постоянная, e — заряд электрона.


