
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрокинетические явления и строение двойного электрического слояСодержание книги
Поиск на нашем сайте
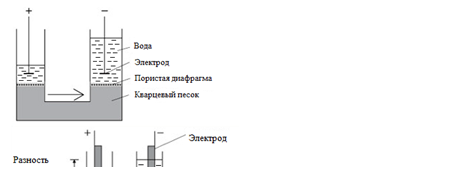
В 1809 г. профессор Московского университета Фердинанд Фридрих фон Рейсс, исследуя электролиз, провел два опыта, сыгравших в дальнейшем значительную роль при изучении свойств коллоидных систем. В первом опыте Рейсс заполнил среднюю часть U-образной стеклянной трубки кварцевым песком, залил водой и ввел металлические электроды. При пропускании постоянного тока им было замечено поднятие уровня воды в колене трубки с отрицательным электродом (рисунок 6.1 a).
В другом опыте, где две стеклянные трубки были погружены в сырую глину и залиты водой, при пропускании тока происходил отрыв частиц глины от ее поверхности и перемещение их к положительному электроду (рисунок 6.1 b). Первое явление – переносдисперсионной среды (воды), несущей положительный заряд, в электрическом поле через неподвижную дисперсную фазу (слой кварцевого песка) было названо электроосмосом, а второе – перемещение отрицательно заряженных частиц дисперсной фазы в электрическом поле – электрофорезом. Позже немецкий врач Генрих Ирениус Квинке (1859 г.) обнаружил, что при продавливании воды или разбавленного раствора электролита через пористую мембрану на ней возникает разность потенциалов, пропорциональная приложенному давлению. Это, обратное электроосмосу, явление получило название потенциала протекани я. Наконец, немецким физиком Фридрихом Эрнстом Дорном (1878 г.) было установлено, что при осаждении (седиментации) высокодисперсного порошка в воде возникает скачок потенциала между электродами, расположенными на разных уровнях. Это явление, обратное электрофорезу, было названо потенциалом осаждения (седиментации), Перечисленные явления, названные электрокинетическими явлениями, широко изучаются и находят практическое применение. Электрокинетическими эти явления были названы потому, что в них обнаруживалась связь между скоростью движения одной из фаз относительно другой фазы, т.е. кинетикой, и скачком электрического потенциала на границе раздела фаз. Объяснение природы электрокинетических явлений, в частности, электроосмоса, было сделано на основании предположения о существовании на границе раздела фаз двойного электрического слоя (ДЭС). Причинами образования ДЭС являются: - избирательная адсорбция ионов из раствора (дисперсионной среды) поверхностью твердых частиц (дисперсной фазы) или диссоциация поверхностных молекул дисперсной фазы (знак заряда поверхности определяют по правилу Панета-Фаянса-Пескова, приведенному ниже); - ориентирование полярных молекул в поверхностном слое. По этому механизму ДЭС образуется, если вещества, составляющие фазы системы не могут обмениваться ионами. В этом случае знак заряда поверхности определяют по правилу Кёна, гласящему, что из двух соприкасающихся фаз положительно заряжается та, которая имеет большую диэлектрическую проницаемость. Благодаря наличию двойного электрического слоя на границе раздела фаз в дисперсных системах наблюдаются электрокинетические явления, к которым относятся электрофорез, электроосмос, потенциал седиментации (эффект Дорна), потенциал течения. Электроосмос – явление перемещения жидкости в пористых телах под действием электрического поля. Электрофорез – явление перемещения частиц дисперсной фазы в электрическом поле. Потенциал течения – явление возникновения разности потенциалов при течении жидкости через пористые тела. Потенциал оседания – явление возникновения разности потенциалов при оседании частиц суспензии. Объяснение явлений, обусловленных существованием ДЭС, возможно на основе теории, описывающей его структуру. Первая теория строения ДЭС была предложена в 1879 г. немецким физиком Л. Гельмгольцем (Герман Людвиг Фердинанд фон Гельмгольц). Эта теория получила развитие в работах французского физика и физико-химика Жана Батиста Перрена (1904 г.). Теория Гельмгольца-Перрена рассматривала ДЭС как плоский конденсатор (рисунок 6.2 a), одна обкладка которого – твердая поверхность, а другая расположена внутри раствора на расстоянии d и параллельна твердой поверхности коллоидной частицы. В соответствии с этой моделью поверхностный потенциал j0 можно рассчитать по формуле
где ρ – поверхностная плотность заряда, С – емкость единицы площади раздела фаз, d – расстояние между обкладками конденсатора, e – диэлектрическая постоянная среды.
Падение потенциала в ДЭС происходит линейно в соответствии с теорией плоского конденсатора от значения j0 на твердой поверхности (x =0) до 0 при x =d (рисунок 6.2 a). При рассмотрении двойного слоя как плоского конденсатора предполагалось, что внутренняя обкладка его образована зарядами, фиксированными на поверхности твердого тела, а внешняя – зарядами, находящимися в жидкости. Считалось, что количество потенциалопределяющих ионов и противоионов в двойном электрическом слое эквивалентно. Ионы рассматривались как точечные заряды. Предполагалось, что слой жидкости, непосредственно прилегающий к поверхности, остается неподвижным в электрическом поле. Толщина двойного электрического слоя считалась незначительной и соответствовала примерно двум молекулярным слоям. В теории Гельмгольца-Перрена не учитывалось тепловое движение ионов, и предпосылка об эквивалентности количества потенциалопределяющих и противоионов в двойном электрическом слое оказалась несостоятельной. Она не могла объяснить существование электрокинетических явлений, перезарядку коллоидных частиц, коагуляцию. Другими словами, эта теория не объясняла результатов экспериментально наблюдаемых явлений. Более совершенная теория строения ДЭС появилась только в начале XX в., она была предложена независимо друг от друга французским физиком Луи Георгом Гуи (1910 г.) и английским электрохимиком Дэвидом Чепменом (1913 г.), которые учли, что избыток ионов одинакового знака не может быть сосредоточен на межфазной границе. Вследствие теплового движения ионы распределяются в виде диффузионной оболочки около твердой поверхности коллоидных частиц. Протяженность этой оболочки зависит от электростатического взаимодействия противоионов с потенциалопределяющими ионами, с одной стороны, и теплового движения противоионов – с другой. Конкуренция электростатических взаимодействий и теплового движения ионов приводит к плавному изменению потенциала внутри ДЭС от величины j0 на твердой поверхности до нуля внутри раствора. При этом в пределах ДЭС концентрация ионов, одноименных с потенциалопределяющими, изменяется от нуля до величины, соответствующей их концентрации в растворе. Одновременно с этим концентрация противоионов, имеющая максимальную величину вблизи поверхности раздела фаз, снижается до величины, равной концентрации ионов противоположного заряда для симметричных электролитов (т.е., электролитов с одинаковым по величине зарядом ионов) или эквивалентной ей (для несимметричных электролитов). Распределение противоионов в диффузионной части двойного ионного слоя зависит от их природы, концентрации электролитов в растворе и от температуры. В теории Гуи-Чепмена принято, что это распределение подчиняется закону Больцмана:
где Объёмная плотность заряда ρ x в точке с координатой х диффузного слоя описывается уравнением
Суммарная объемная плотность заряда по всему раствору ρ=0 (условие электронейтральности раствора):
При выводе уравнения зависимости потенциала 1) ДЭС является плоским, т.е. радиус кривизны поверхности коллоидной частицы значительно больше толщины двойного слоя; 2) диэлектрическая проницаемость растворителя в пределах ДЭС постоянна, т.е. она не зависит от расстояния до поверхности частицы; 3) при переходе ионов из объема раствора в точку, расположенную на расстоянии х от твердой поверхности работа совершается только против сил электрического взаимодействия; 4) собственный объем ионов исчезающе мал, т.е. рассматриваются точечные заряды; 5) распределение ионов в пределах двойного электрического слоя подчиняется закону Больцмана. Для симметричного бинарного электролита, для которого z+ =z– =z было получено уравнение для поверхностей с потенциалом не более 50·10-3 В, связывающее поверхностную плотность заряда ρ s с потенциалом j0:
где e – диэлектрическая постоянная среды, κ – параметр Дебая, C 0 - концентрация ионов в растворе. Потенциал с удалением от заряженной твердой поверхности изменяется экспоненциально:
где j x – потенциал на расстоянии x от твердой поверхности. Величина 1/κ – величина, обратная толщине диффузной части ДЭС. Подстановка величины x =1/κ в уравнение (6.7) приводит к значению Современные представления о строении двойного электрического слоя развиты в теории Штерна. В соответствии с теорией Штерна двойной электрический слой состоит из двух частей – плотной и диффузной. Как уже было сказано, двойной электрический слой образуется за счет избирательной адсорбции ионов из раствора поверхностью коллоидных частиц или за счет диссоциации поверхностных молекул. Те ионы, которые придают заряд твердой поверхности, принято называть потенциалопределяющими ионами, а ионы, переходящие в раствор или остающиеся в растворе – противоионами. Согласно теории Штерна, в плотной части двойного слоя противоионы удерживаются электрическими или адсорбционными силами и располагаются на некотором расстоянии d от поверхности. Плотную часть двойного электрического слоя иногда называют слоем Гельмгольца, а d– толщиной слоя Гельмгольца. В плотной части двойного электрического слоя происходит линейное падение потенциала заряженной поверхности от значения j0до значения jd. В диффузной части двойного электрического слоя концентрация противоионов уменьшается экспоненциально благодаря их тепловому движению. Падение потенцнала в диффузной части двойного электрического слоя также происходит по экспоненте. Диффузную часть двойного электрического слоя иногда называют слоем Гуи. При перемещении дисперсной фазы и дисперсионной среды относительно друг друга независимо от причин, его вызвавших, происходит разрыв двойного электрического слоя по плоскости скольжения, плоскость скольжения обычно проходит по диффузному слою и часть его ионов остается в дисперсионной среде. В результате дисперсная фаза и дисперсионная среда оказываются противоположно заряженными. Плоскость скольжения может находиться на разном расстоянии от поверхности раздела фаз. Это расстояние зависит от скорости движения фаз, от вязкости среды, природы фаз и других факторов. Потенциал плоскости скольжения получил название электрокинетического или z (дзета)- потенциала. Строение двойного электрического слоя по Штерну приведено на рисунке 6.2 с (D – расстояние, на котором находится граница скольжения между дисперсной фазой и дисперсионной средой, z – электрокинетический потенциал). По теории Штерна, ионы, образующие ДЭС, распределяются в нем не только под действием сил электростатического взаимодействия и теплового движения, но и под влиянием адсорбционного взаимодействия с твердой поверхностью. Для учета этого взаимодействия Штерн использовал введенное им понятие «специфического» адсорбционного потенциала. Исследования показали, что адсорбционные силы могут быть настолько значительными, что могут приводить к сверхэквивалентной адсорбции на поверхности поливалентных противоионов по отношению к потенциалопределяющим ионам. Образующийся адсорбционный слой, как правило, мономолекулярный. В результате специфической адсорбции на межфазной поверхности накапливается такое количество электричества, что потенциал вблизи поверхности на расстоянии d будет отличаться от j0 не только по величине, но и по знаку. Теория Штерна позволила объяснить перезарядку коллоидных частиц, что было недоступно теориям Гельмгольца-Перрена и Гуи-Чепмена. Главным в модели ДЭС по Штерну является разделение двойного слоя на две части, внутреннюю (плотная часть или слой Гельмгольца) и внешнюю (диффузная часть или слой Гуи). Таким образом, Штерн не только объединил две более ранние теории строения двойного слоя, но и развил их, введя понятие о специфической адсорбции ионов в плотной части ДЭС. Плотная часть ДЭС по Штерну образована специфически адсорбированными ионами. Полное падение потенциала в пределах двойного слоя складывается из падения потенциала в плотной части и падения потенциала в диффузионной части ДЭС. Внутреннюю (плотную) часть ДЭС Штерн описал на основании теории мономолекулярной адсорбции Ленгмюра, расширив представление об адсорбции ионов на активных участках поверхности раздела фаз. Потенциал jd часто называют штерновским. Во внешней, диффузной части адсорбционные силы и собственный размер гидратированных ионов не учитываются, так как предполагается, что протяженность действия сил, обусловливающих специфическую адсорбцию, в отличие от электростатических, столь мала, что учет их важен только на расстоянии, соответствующем размеру гидратированного иона. Распределение потенциала в диффузной части двойного слоя описывается уравнением теории Гуи-Чепмена. Положение плоскости скольжения в модели Штерна остается неопределенным. Часто полагают, что плоскость скольжения совпадает с границей, разделяющей слой Штерна и слой Гуи. Однако в более общем случае считается, что плоскость скольжения проходит в слое Гуи. Теория Штерна применима не только к твердым частицам с четко выраженной границей раздела, но и к системам, в которых граница раздела фаз размыта, например, к волокнам, набухающим в водных растворах, или отсутствует, что характерно для растворов белков и полиэлектролитов. В любом случае, в системе должно устанавливаться электрохимическое равновесие. При большом количестве ионогенных групп или активных центров на частицах коллоидной фазы уравнение закона действующих масс, используемое для описания степени диссоциации поверхностных ионогенных групп и уравнение изотермы адсорбции Ленгмюра совпадают. Это позволяет использовать теорию Штерна для описания процессов в разнообразных дисперсных системах. Потенциалопределяющими ионами при получении золей будут ионы, которые удовлетворяют эмпирическому правилу Панета-Фаянса-Пескова: на поверхности агрегата в первую очередь адсорбируются ионы, которые - входят в состав агрегата; - способны достраивать кристаллическую решетку агрегата; - образуют труднорастворимое соединение с ионами агрегата; - изоморфны с ионами агрегата. Примером двойного электрического слоя, образовавшегося вокруг частицы твердого вещества, может служить двойной электрический слой, возникающий на кристалликах йодида серебра, полученного по реакции:
в присутствии избытка йодида калия. При этом на поверхности частицы
В случае избытка AgNO3 в достройке кристалла AgI участвуют уже ионы Ag+. Поверхность частицы заряжается положительно, к ней притягиваются противоионы NO3-, образуя двойной электрический слой. Строение мицеллы в этом случае имеет вид: { [(AgI) m ] n Ag+ (n – x)NO3-} х + x NO3-. Возникновение двойного электрического слоя за счет ионизации можно проиллюстрировать образованием двойного электрического слояна кристалликах водного золя диоксида кремния. Молекулы SiO2, находящиеся на поверхности таких кристалликов, взаимодействуют с водой, образуя кремневую кислоту, которая ионизируется по уравнению: Н2SiO3 При этом ионы
|
|||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 , (6.1)
, (6.1)
 , (6.2)
, (6.2)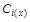 ,
,  – концентрация ионов i -го вида на расстоянии x от твердой поверхности и в объеме раствора, соответственно; Wi = ziF j x – работа перемещения 1 кг - экв ионов i -го вида с бесконечно большого расстояния в точку с координатой x ДЭС; zi – заряд ионов i -го вида (с учетом знака); F – число Фарадея; j x – потенциал в точкес координатой x ДЭС; R – универсальная газовая постоянная, T – температура.
– концентрация ионов i -го вида на расстоянии x от твердой поверхности и в объеме раствора, соответственно; Wi = ziF j x – работа перемещения 1 кг - экв ионов i -го вида с бесконечно большого расстояния в точку с координатой x ДЭС; zi – заряд ионов i -го вида (с учетом знака); F – число Фарадея; j x – потенциал в точкес координатой x ДЭС; R – универсальная газовая постоянная, T – температура. . (6.3)
. (6.3) . (6.4)
. (6.4) от расстояния x в теории Гуи-Чепмена были сделаны следующие предположения:
от расстояния x в теории Гуи-Чепмена были сделаны следующие предположения: , (6.5)
, (6.5) , (6.6)
, (6.6) , (6.7)
, (6.7) , т.е. толщиной диффузного слоя является такое расстояние от твердой поверхности, на котором потенциал в e раз меньше, чем j0.
, т.е. толщиной диффузного слоя является такое расстояние от твердой поверхности, на котором потенциал в e раз меньше, чем j0.
 лучше адсорбируются ионы, входящие в состав частиц твердой фазы или изоморфные с ними (правило Панета-Фаянса-Пескова), в данном случае, это – анионы йода I–. Таким образом, частица оказывается заряженной отрицательно и к ней притягиваются ионы противоположного знака (катионы K+) – в итоге образуется ДЭС.
лучше адсорбируются ионы, входящие в состав частиц твердой фазы или изоморфные с ними (правило Панета-Фаянса-Пескова), в данном случае, это – анионы йода I–. Таким образом, частица оказывается заряженной отрицательно и к ней притягиваются ионы противоположного знака (катионы K+) – в итоге образуется ДЭС.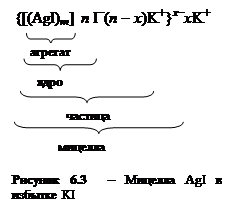 Полученный коллоидный раствор называется золем иодида серебра, а частицы
Полученный коллоидный раствор называется золем иодида серебра, а частицы  .
. остаются на поверхности частицы, придавая ей отрицательный заряд, а ионы водорода переходят в раствор. Строение мицелл SiO2 в водном растворе может быть представлено следующей формулой (рисунок 6.4):
остаются на поверхности частицы, придавая ей отрицательный заряд, а ионы водорода переходят в раствор. Строение мицелл SiO2 в водном растворе может быть представлено следующей формулой (рисунок 6.4):



