
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проведение седиментационного анализа на приборе фигуровскогоСодержание книги
Поиск на нашем сайте
Цель работы: построить интегральную и дифференциальную кривую распределения частиц суспензии по размерам. Определить наиболее вероятный радиус частиц и их содержание в суспензии. Ход работы. Чаще всего определение скорости оседания суспензии осуществляют весовым методом – путем периодического или непрерывного взвешивания осадка, собирающегося на дне сосуда для осаждения.
Наиболее простым и чувствительным прибором для этой цели являются седиментационные весы Фигуровского. Прибор (рисунок 7.1) состоит из стеклянного или кварцевого коромысла 1, на тонком конце которого имеется крючок, к которому на длинной и тонкой стеклянной нити 2 подвешивается легкая стеклянная чашечка 3 с несколько загнутыми краями. Чашечка погружается в цилиндр с анализируемой дисперсной системой. Оседающие на чашечку частицы увеличивают ее массу и вызывают дополнительную деформацию коромысла весов, которую фиксируют во времени с помощью отсчетного микроскопа. Работа с прибором очень проста. После заполнения цилиндра исследуемой суспензией на крючок коромысла подвешивают чашечку и проверяют: * расположение чашечки относительно стенок цилиндра – она должна располагаться примерно по центру сечения цилиндра и ни в коем случае не должна их касаться; * глубина погружения чашечки в суспензию должна составлять примерно 10-15 см или несколько более; * настройка отсчетного микроскопа должна быть выполнена так, чтобы точка, по которой будут производиться замеры деформации коромысла (обычно кончик крючка коромысла), находилась в нижней части шкалы (обратное изображение). Теперь все готово для того, чтобы начать эксперимент за исключением изучаемой дисперсной системы, часть частиц которой за время настройки уже осела. Поэтому аккуратно, чтобы не нарушить настройку, снимают чашечку с крючка и вынимают ее из цилиндра. Затем стеклянной палочкой, на кончик которой надет отрезок резиновой трубки, производят взбалтывание системы. Стеклянную палочку надо перемещать вверх-вниз по всей высоте цилиндра. Считается, что за 2-3 минуты непрерывного перемешивания получается вполне равномерное распределение дисперсной фазы по всему объему цилиндра. Немедленно после окончания перемешивания: * в цилиндр опускают чашечку и подвешивают ее на крючок коромысла; * если необходимо, быстро корректируют (вверх/вниз) шкалу отсчетного микроскопа, (при этом точка отсчета не обязательно! должна установиться точно на нулевое деление шкалы); * включают секундомер и записывают в таблицу данные 1-го отсчета (в делениях шкалы микроскопа) для времени начала опыта равного нулю. Первый отсчет делают не позднее 15-20 с после включения секундомера. Далее делают 3 отсчета через каждые 15 с, 4 отсчета через 30 с, 4 – через каждые 60 с, затем интервал времени между отсчетами увеличивают до 3, 5, 10 мин и т.д. Опыт прекращают после прекращения деформации коромысла, т. е. когда два последовательных отсчета по микроскопу совпадут. Результаты наблюдений записывают в таблицу 7.1.
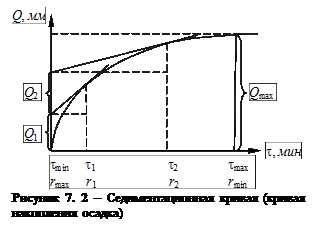
По окончании опыта линейкой измеряют глубину погружения чашечки H (рисунок 7.1). При этом, если исследуемая суспензия не осветлилась и чашечку не видно, необходимо аккуратно сдвинуть несколько в сторону цилиндр так, чтобы через его стенку подвешенная чашечка стала видна. Обработка результатов 1. По данным таблицы 7.1 в Excel строят седиментационную кривую (кривую накопления осадка) Q = f (t), причем на оси абсцисс откладывают время в с (или в мин), а по оси ординат – величину деформации коромысла весов. Величина деформации коромысла Q в пределах справедливости закона Гука пропорциональна массе осадка, выпавшего на чашечку. Вид седиментационной кривой представлен на рисунке 7.2.
3. Определяют максимальный и минимальный радиусы частиц исследуемой дисперсной системы. Для нахождения 4. Далее, к 4 ¸ 5 точкам седиментационной кривой (рисунок 7.2), соответствующим моментам времени
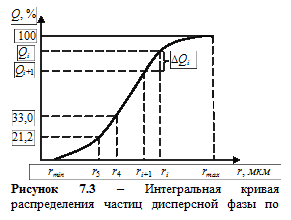
5. По данным таблицы 7.2 строят интегральную кривую распределения частиц дисперсной фазы по размерам (рисунок 7.3). Для этого по оси ординат откладывают суммарное содержание фракции D Q, начиная с наиболее мелких частиц, а по оси абсцисс – радиусы, соответствующие большему радиусу данной фракции. Например, если в дисперсной системе содержится 21,2% частиц с радиусами Интегральная кривая распределения позволяет определить процентное содержание фракции с радиусами частиц, лежащими в интервале от ri до ri +1 (i =1, 2, …). Как следует из рисунка 7.3, процентное содержание фракций с радиусами частиц от ri до ri+ 1будет равно D Qi.
Соединяя середины верхних оснований прямоугольников, получим дифференциальную кривую распределения частиц по размерам (радиусам).
Выводы. 1. Анализируемая дисперсная система содержит частицы с радиусами от r min =… до r max = …. 2. Площадь под всей дифференциальной кривой распределения дает общее количество всех частиц дисперсной системы, выраженное в % (Q = 100%). 3. По дифференциальной кривой распределения можно определить содержание частиц (в %) с радиусами в интервале от ri до ri +1 (площадь под кривой на рисунке 7.5 в диапазоне радиусов от ri до ri +1. 4. Максимум кривой распределения соответствует наиболее вероятному размеру (радиусу) частиц данной дисперсной системы (т.е. процентное содержание таких частиц в данной дисперсной системе самое большое).
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 833; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.208.220 (0.009 с.) |

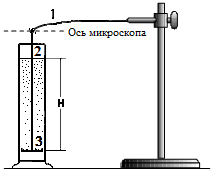 Рисунок 7.1 –Прибор Фигуровского
Рисунок 7.1 –Прибор Фигуровского
 2. Рассчитывают константу К (значения вязкости дисперсионной среды, плотности дисперсной фазы и дисперсионной среды необходимо взять у лаборанта или у преподавателя).
2. Рассчитывают константу К (значения вязкости дисперсионной среды, плотности дисперсной фазы и дисперсионной среды необходимо взять у лаборанта или у преподавателя).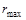 проводят касательную к седиментационной кривой из начала координат. Конец прямолинейного участка кривой, т.е. точка отрыва касательной от седиментационной кривой дает время
проводят касательную к седиментационной кривой из начала координат. Конец прямолинейного участка кривой, т.е. точка отрыва касательной от седиментационной кривой дает время 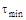 , соответствующее
, соответствующее 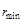 вычисляется по времени
вычисляется по времени 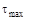 , соответствующему той точке, в которой кривая накопления переходит в прямую, параллельную оси абсцисс, т.е. моменту времени, в который оседание полностью закончилось (рисунок 7.2). Радиусы
, соответствующему той точке, в которой кривая накопления переходит в прямую, параллельную оси абсцисс, т.е. моменту времени, в который оседание полностью закончилось (рисунок 7.2). Радиусы 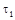 ,
, 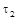 и т.д., проводят касательные, продолжая их до пересечения с осью ординат. Для построения касательных выбирают участки кривой с наибольшей кривизной.[2] По уравнению (7.4) рассчитывают радиусы частиц, полностью осевших ко времени
и т.д., проводят касательные, продолжая их до пересечения с осью ординат. Для построения касательных выбирают участки кривой с наибольшей кривизной.[2] По уравнению (7.4) рассчитывают радиусы частиц, полностью осевших ко времени 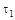
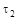 …
…
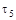
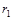
 …
…
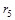
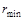
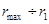
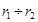 …
…
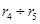
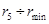
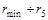 (таблица 7.2), то по оси ординат откладывают 21,2%, а по оси абсцисс – r 5. Если следующая фракция имеет размеры частиц в диапазоне r 5 ¸ r 4 и ее содержание составляет 11,8%, то по оси ординат откладывают суммарное процентное содержание обеих фракций, т.е. 21,2+11,8 = 33,0%, а по оси абсцисс – r 4 и т.д.
(таблица 7.2), то по оси ординат откладывают 21,2%, а по оси абсцисс – r 5. Если следующая фракция имеет размеры частиц в диапазоне r 5 ¸ r 4 и ее содержание составляет 11,8%, то по оси ординат откладывают суммарное процентное содержание обеих фракций, т.е. 21,2+11,8 = 33,0%, а по оси абсцисс – r 4 и т.д.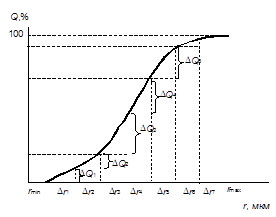 Рисунок 7.4 –Обработка интегральной кривой распределения (D ri = 2 мкм)
Рисунок 7.4 –Обработка интегральной кривой распределения (D ri = 2 мкм)
 6. Более наглядное представление о распределении частиц исследуемой дисперсной системы по размерам дает дифференциальная кривая распределения. Для этого по интегральной кривой распределения находят величины приращения процентного содержания частиц D Qi, приходящиеся на равные интервалы радиусов, например на D r = 2 мкм (рисунок 7.4). Для этого весь диапазон размеров частиц от rmin до rmax разбивают на равные интервалы D r и находят для каждого интервала соответствующее ему приращение процентного содержания фракции D Q. Найденные величины D Q 1,D Q 2,D Q 3 и т.д. записывают в таблицу 7.3. По данным таблицы 7.3 строят дифференциальную кривую распределения частиц дисперсной системы по размерам. Для этого в координатах
6. Более наглядное представление о распределении частиц исследуемой дисперсной системы по размерам дает дифференциальная кривая распределения. Для этого по интегральной кривой распределения находят величины приращения процентного содержания частиц D Qi, приходящиеся на равные интервалы радиусов, например на D r = 2 мкм (рисунок 7.4). Для этого весь диапазон размеров частиц от rmin до rmax разбивают на равные интервалы D r и находят для каждого интервала соответствующее ему приращение процентного содержания фракции D Q. Найденные величины D Q 1,D Q 2,D Q 3 и т.д. записывают в таблицу 7.3. По данным таблицы 7.3 строят дифференциальную кривую распределения частиц дисперсной системы по размерам. Для этого в координатах 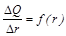 на график наносят серию прямоугольников, основания которых равны 2 мкм, а высоты – величинам отношений
на график наносят серию прямоугольников, основания которых равны 2 мкм, а высоты – величинам отношений 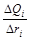 для данных диапазонов размеров частиц D ri (рисунок 7.5).
для данных диапазонов размеров частиц D ri (рисунок 7.5).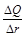
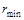 ¸ (
¸ ( Рисунок 7.5 –Дифференциальная кривая распределения частиц дисперсной системы по размерам (D r = ri +1 – ri = 2 мкм)
Рисунок 7.5 –Дифференциальная кривая распределения частиц дисперсной системы по размерам (D r = ri +1 – ri = 2 мкм)



