
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическое выражение для седиментационной кривой и его использование при обработке экспериментальных данныхСодержание книги
Поиск на нашем сайте
Нанесение касательных графическим путем является очень трудоемким, субъективным методом и сопряжено с существенными ошибками, особенно в области наименьших значений радиуса кривизны кривой. Поэтому вполне разумной представляется идея найти аналитическое выражение функции распределения в интегральной и дифференциальной форме. Будучи свободным от ошибок, вызванных эмпирическими приемами обработки кривой накопления, оно позволяет всесторонне изучать особенности дисперсных систем. Форма седиментационной кривой такова, что формально ее можно описать уравнением вида:
где Физический смысл обеих констант легко устанавливается. Во-первых, если положить Q = Qm /2, то t = t1/2, т.е. t1/2 является «временем половинной седиментации». Во-вторых, если t ® ¥, то в знаменателе можно пренебречь величиной t1/2 по сравнению с t, и тогда Q = Qm, т.е. Qm является предельным (суммарным) значением массы частиц дисперсной фазы. Общая масса Q дисперсной фазы на дне сосуда ко времени t, таким образом, составит: Q = Q 0 + q, (7.7) где Q 0 – масса осевших частиц дисперсной фазы, q – масса еще оседающих частиц дисперсной фазы. Скорость накопления дисперсной фазы в этот момент времени выразится как
Это уравнение представляет собой уравнение касательной к одной из точек кривой седиментации (кривой осаждения, накопления): Q 0 – отрезок на оси ординат, соответствующий количеству дисперсной фазы, нацело выпавшей к данному моменту времени t, а Для получения аналитического выражения интегральной кривой распределения необходимо выразить в явном виде массу нацело выпавших частиц
Выражение для Q нам известно (уравнение 7.6), а для нахождения производной
Подставляя уравнения (7.6) и (7.10) в уравнение (7.9), после элементарных преобразований получим:
Полученное уравнение станет уравнением интегральной кривой распределения, если аргумент tзаменить через радиус частиц r. Для этого воспользуемся уравнением (7.6), из которого следует, что
где r по физическому смыслу представляет собой радиус частиц, выпадающих ко времени половинной седиментации t1/2. Подставляя выражения (7.12) в (7.11), получим аналитическое выражение интегральной кривой распределения:
Чтобы получить уравнение дифференциальной кривой распределения надо, очевидно, продифференцировать по r уравнение (7.13). Результат дифференцирования дает аналитическое выражение дифференциальной кривой распределения в виде:
Точке максимума на дифференциальной кривой распределения (точке перегиба на интегральной кривой распределения) соответствует так называемый наиболее вероятный радиус частиц r 0, величину которого нетрудно вычислить. Для этого необходимо функцию F (уравнение 7.14) продифференцировать по r и приравнять производную нулю. В результате получим следующее уравнение для расчета наиболее вероятного радиуса:
Иногда при выполнении седиментационного анализа определяют еще два радиуса: максимальный и минимальный, т.е. находят размеры наиболее крупных частиц и самых мелких. Основная трудность, которую при этом надо преодолеть, заключается в достаточно обоснованном выборе времени осаждения этих частиц. Чаще всего для нахождения максимального r max радиуса частиц проводят касательную к седиментационной кривой из начала координат. Конец прямолинейного участка кривой, т.е. точка отрыва касательной от кривой седиментации и дает время tmax (рисунок 7.2) соответствующее r max. Имея аналитическое выражение для седиментационной кривой (7.8), нетрудно найти и аналитическое выражение для касательной, проведенной к этой кривой из начала координат. Это уравнение имеет вид:
Минимальный радиус определяют аналогичным образом, но касательную проводят к кривой там, где она переходит в прямую параллельную оси абсцисс. В действительности понятие минимального радиуса в полидисперсных системах весьма неопределенно (скорее, не имеет физического смысла, так как, в действительности очень мелкие частицы не осаждаются из-за участия в броуновском движении). Уравнения (7.13) и (7.14) содержат константы Qm и r, которые должны быть определены на основании экспериментальных исследований седиментации конкретной дисперсной системы. Для этого перепишем уравнение (7.8) в виде:
Это уравнение в координатах
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.202.48 (0.005 с.) |

 , (7.6)
, (7.6) и t1/2 - константы.
и t1/2 - константы.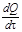 , а ее масса q как
, а ее масса q как  :
: . (7.8)
. (7.8)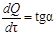 - угловой коэффициент. Типичная седиментационная кривая (кривая накопления) представлена на рисунке 7.2.
- угловой коэффициент. Типичная седиментационная кривая (кривая накопления) представлена на рисунке 7.2. в любой момент времени t. Для этого перепишем уравнение касательной (7.8) в виде:
в любой момент времени t. Для этого перепишем уравнение касательной (7.8) в виде: . (7.9)
. (7.9) продифференцируем (7.6) по t:
продифференцируем (7.6) по t: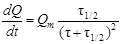 . (7.10)
. (7.10) . (7.11)
. (7.11)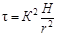 и
и  , (7.12)
, (7.12)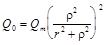 . (7.13)
. (7.13)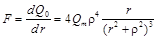 . (7.14)
. (7.14) . (7.15)
. (7.15)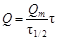 . (7.16)
. (7.16) . (7.17)
. (7.17) является уравнением прямой, константы которого (Qm – котангенс угла наклона прямой; t1/2/ Qm – отрезок, отсекаемый на оси ординат) легко определяются из графика (приближенно) или аналитически методом наименьших квадратов.
является уравнением прямой, константы которого (Qm – котангенс угла наклона прямой; t1/2/ Qm – отрезок, отсекаемый на оси ординат) легко определяются из графика (приближенно) или аналитически методом наименьших квадратов.


