
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика приготовления золя диоксида марганцаСодержание книги
Поиск на нашем сайте
Золь диоксида марганца получают методом химической конденсации по реакции восстановления перманганата калия тиосульфатом натрия: 8КМnO4 + 3 Na2S2O3 + Н2O ® 8 MnO2 + Na2SO4 + 3K2SO4 + 2KOH Для получения золя диоксида марганца в мерной колбе готовят 250 мл раствора перманганата калия, разбавляя 100 мл 0,01 М КМnО4 водой до метки. Переливают раствор КМnО4 в стакан и туда медленно вводят 15 мл 0,125%-ного раствора тиосульфата натрия. При этом образуется золь диоксида марганца темно-вишневого цвета. Ход работы: Для проведения работы готовят 2 серии по 10 пробирок, нумеруют их. В 10 пробирок первой серии наливают по 5 мл золя диоксида марганца. В 10 пробирках второй серии готовят растворы электролита разной концентрации последовательным разбавлением. Для этого в первую пробирку наливают 4 мл исходного раствора электролита, из нее отбирают 2 мл в следующую пробирку и туда же добавляют 2 мл дистиллированной воды. Из второй пробирки также отбирают 2 мл раствора в следующую, третью, пробирку, в которую затем добавляют 2 мл дистиллированной воды и т. д. Таким же образом готовят 10 растворов электролита по 2 мл. После приготовления растворов электролита отмечают время и добавляют эти растворы в пробирки с золем. Полученные смеси встряхивают и оставляют на 15 минут. При добавлении растворов электролитов в пробирки с золем необходимо точно соблюдать последовательность расположения пробирок по возрастанию концентрации добавленного электролита! Через 15 минут в некоторых пробирках произойдет коагуляция, о которой можно судить по помутнению золя или по выпадению осадка. Результаты наблюдений за изменениями в пробирках с золем и электролитом записывают в таблицу 6.3. В графе "Вид системы" указывают образование осадка, помутнение, прозрачность.
Таблица 6.3 - Результаты наблюдений за изменениями в пробирках с золем и электролитом Электролит............................................ (название, концентрация)
Порог коагуляции определяют по концентрации электролита между пробирками с прозрачным золем и помутневшим. Предположим, что через 15 минут после добавления раствора электролита в 5-ой пробирке золь прозрачный, а в 6-ой – мутный. Вычисляют концентрации растворов электролита в этих пробирках по соотношению: где V 1 и C 1 - объем и концентрация исходного раствора электролита, а V 2 и C 2 -его концентрация после добавления к золю. Например, для 0,4 М раствора ВаСl2, если порог коагуляции лежит между концентрациями растворов электролита в 5-ой и 6-ой пробирках: С5 = (0,04×2)/(16×7) = 7,14×10-4 моль / л; С6 = (0,04×2)/(32×7) = 3,57×10-4 моль / л. Порог коагуляции С к=(С 5 + С 6)/ 2 =5,355×10-4 моль / л. Аналогичные опыты проводят с каждым из электролитов. По полученным концентрациям С кпроверяют правило Шульце-Гарди.
7. Седиментационный анализ суспензий и эмульсий
В практике бурения скважин и их эксплуатации широко используют различные промывочные жидкости и цементные растворы, нефтяные эмульсии, пены и ряд других микрогетерогенных систем. Одной из наиболее важных характеристик таких систем является их полидисперсность, поэтому для теории и практики важно знать фракционный состав таких систем, то есть количественное распределение частиц по их размерам (радиусам). Несмотря на относительно малое содержание частиц с коллоидными размерами в указанных выше системах, их присутствие во многом определяет физико-механические и реологические свойства таких систем. Это объясняется тем, что на фракцию частиц с коллоидными размерами приходится большая часть общей межфазной поверхности. Учет и исследование этого фактора имеет большое значение при приготовлении и регулировании свойств дисперсных систем, применяемых в нефтепромысловом деле, а также при расчете и конструировании электродегидраторов, отстойных и очистных устройств. Знание характеристик дисперсности необходимо также для расчета запасов нефти в нефтяных коллекторах (определение свободного межпорового пространства). Одним из важнейших методов исследования полидисперсных систем является седиментационный анализ, дающий возможность находить так называемую “функцию распределения”, то есть, определять относительное содержание частиц в системе с найденными размерами (радиусами).
Принцип седиментационного анализа состоит в измерении скорости оседания частиц дисперсной фазы в какой-либо дисперсионной среде. В основе седиментационного анализа лежит закон Стокса, по которому сила трения
Если частица движется под действием силы тяжести, и сила трения уравновешивает силу тяжести, действующую на частицу, и выталкивающую силу Архимеда, то она движется равномерно:
где D и d – плотность дисперсной фазы и дисперсионной среды, соответственно; g – ускорение силы тяжести (9,81 м / c 2). Из уравнения (7.2) получим:
Закон Стокса выведен для равномерного движения сферических частиц в вязкой среде и применим к частицам, диаметр которых меньше 100 мкм, но больше 0,1 мкм, так как частицы, диаметр которых меньше 0,1 мкм, обладают заметным броуновским движением, а частицы с диаметром, большим 100 мкм, движутся равномерно ускоренно. Таким образом, закон Стокса применим к системам с низкой степенью дисперсности - суспензиям и эмульсиям. Для данной дисперсной фазы и дисперсионной среда величины h, D и d постоянны. Тогда
Так как скорость оседания суспензии
Следует обратить внимание, что константа К имеет размерность м 1/2 с 1/2, если все величины под корнем в формуле (7.4) выражены в системе СИ:
Радиус частицы, рассчитанный по формуле (7.4) с учетом размерности H (м) и t (с) будет выражен в м. Так как радиус частицы, выраженный в м, величина очень маленькая, то ее удобно выражать в микрометрах (мкм): 1 м = 106 мкм.
Лабораторная работа №7.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.91.108 (0.011 с.) |

 ,
, , возникающая при движении сферической частицы радиусом r со скоростью uв среде с вязкостью h выражается уравнением:
, возникающая при движении сферической частицы радиусом r со скоростью uв среде с вязкостью h выражается уравнением: . (7.1)
. (7.1) . (7.2)
. (7.2)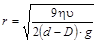 . (7.3)
. (7.3) и
и  .
. , то есть, равна пройденному частицами расстоянию Н, деленному на время t, то расчетной формулой для определения радиусов частиц будет
, то есть, равна пройденному частицами расстоянию Н, деленному на время t, то расчетной формулой для определения радиусов частиц будет . (7.4)
. (7.4) .
.



