Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа перемещения проводника с током в магнитном полеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим участок проводника с током, который может перемещаться в магнитном поле. Поле будем считать однородным и перпендикулярным к плоскости контура. Работа, совершенная силой F при перемещении на x участка проводника l с током I, будет равна: A = Fx = BIlx = IBS = IdФ В случае если поле неоднородно dA = IdФ, где dФ - поток магнитной индукции пересекаемый проводником при движении. Можно показать, что если В не перпендикулярно плоскости контура, то формула для расчета работы будет той же. Формула будет справедлива и для перемещения проводника с током любой формы, в том числе и замкнутого контура с током (в этом cлучае dФ - изменение потока, пересекающего контур). Она справедлива не только для прямолинейного перемещения, но и для перемещения любого типа. Примечания: 1. Если контур перемещается в однородном поле таким образом, что поток его пересекающий остается неизменным, то работа не производится. Работа по перемещению проводника с током совершается за счет энергии источника тока. Естественный и поляризованный свет. Способы поляризации света. Закон Малюса. Закон Брюстера Естественный и поляризованный свет Следствием теории Максвелла является поперечность световых волн: векторы напряженностей электрического? и магнитного Н полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости v распространения волны (перпендикулярно лучу). Поэтому для описания закономерностей поляризации света достаточно знать поведение лишь одного из векторов. Обычно все рассуждения ведутся относительно светового вектора - вектора напряженности Е электрического поля (это название обусловлено тем, что при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества). Свет представляет собой суммарное электромагнитное излучение множества атомов. В данном случае равномерное распределение векторов Е объясняется большим числом атомарных излучателей, а равенство амплитудных значений векторов Е - одинаковой (в среднем) интенсивностью излучения каждого из атомов. Свет со всевозможными равновероятными ориентациями вектора Е (и, следовательно, Н) называется естественным. Свет, в котором направления колебаний светового вектора каким-то образом упорядочены, называется поляризованным. Так, если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное!) направление колебаний вектора Е, то имеем дело с частично поляризованным светом. Свет, в котором вектор Е (и, следовательно, Н) колеблется только в одном направлении, перпендикулярном лучу, называется плоскополяризованным (линейно поляризованным). Способы поляризации света Поляризация - для электромагнитных волн это явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H. Когерентное электромагнитное излучение может иметь: Линейную поляризацию - в направлении, перпендикулярном направлению распространения волны; Круговую поляризацию - правую либо левую, в зависимости от направления вращения вектора индукции; Эллиптическую поляризацию - случай, промежуточный между круговой и линейными поляризациями. Некогерентное излучение может не быть поляризованным, либо быть полностью или частично поляризованным любым из указанных способов. В этом случае понятие поляризации понимается статистически. При теоретическом рассмотрении поляризации волна полагается распространяющейся горизонтально. Тогда можно говорить о вертикальной и горизонтальной линейных поляризациях волны. Теория явления Электромагнитная волна может быть разложена (как теоретически, так и практически) на две поляризованные составляющие, например поляризованные вертикально и горизонтально. Возможны другие разложения, например по иной паре взаимно перпендикулярных направлений, или же на две составляющие, имеющие левую и правую круговую поляризацию. При попытке разложить линейно поляризованную волну по круговым поляризациям (или наоборот) возникнут две составляющие половинной интенсивности. Как с квантовой, так и с классической точки зрения, поляризация может быть описана двумерным комплексным вектором (вектором Джонса). Поляризация фотона является одной из реализаций q-бита. Практическое использование Свет солнца, являющийся тепловым излучением, не имеет поляризации, однако рассеянный свет неба приобретает частичную линейную поляризацию. Поляризация света меняется также при отражении. На этих фактах основаны применения поляризующих фильтров в фотографии и т. д. Линейную поляризацию имеет обычно излучение антенн. По изменению поляризации света при отражении от поверхности можно судить о структуре поверхности, оптических постоянных, толщине образца. Если рассеянный свет поляризовать, то, используя поляризационный фильтр с иной поляризацией, можно ограничивать прохождение света. Интенсивность света прошедшего через поляризаторы подчиняется закону Малюса. На этом принципе работают жидкокристаллические экраны. Некоторые живые существа, например пчёлы, способны различать линейную поляризацию света, что даёт им дополнительные возможности для ориентации в пространстве. Обнаружено, что некоторые животные, например креветка-богомол павлиновая [1] способны различать циркулярно-поляризованный свет, то есть свет с круговой поляризацией Поляриметр - прибор, предназначенный для измерения угла вращения плоскости поляризации оптически активными прозрачными и однородными растворами и жидкостями. Применяется в лабораториях пищевой, химической промышленности и других отраслях науки и производства для определения концентрации растворов оптически активных веществ, таких как сахар, глюкоза, белок, по углу вращения плоскости поляризации. Поляриметр круговой СМ-3 Поляриметр СМ-3 предназначен для измерения угла вращения плоскости поляризации оптически активными прозрачными и однородными растворами и жидкостями с целью определения их концентрации. Поляриметр визуального типа удобен в эксплуатации, обладает высокой надежностью и точностью измерений, соответствует современным эстетическим и эргономическим требованиям. Поляриметр СМ-3 применяется в различных отраслях промышленности: пищевой, химической, полиграфической. Поляриметр П161-М портативный Поляриметр П161-М предназначен для измерения угла вращения плоскости поляризации оптически активными прозрачными и однородными растворами и жидкостями. Поляриметр П161-М применяется в лабораториях пищевой, химической промышленности и других отраслях науки и производства для определения концентрации растворов оптически активных веществ, таких как сахар, глюкоза, белок по углу вращения плоскости поляризации. Полярископ ПКС-250 М Полярископ ПКС-250 М предназначен для определения двойного лучепреломления в плоских заготовках и изделиях из прозрачных и слабоокрашенных материалов. Полярископ ПКС-250 М используется: для количественной оценки величины двойного лучепреломления методом Сенармона с погрешностью не более 10 нм, для оценки распределения двойного лучепреломления в объекте по интерференционной окраске, для исследований распределения двойного лучепреломления в объекте в свете, поляризованном по кругу. Достоинства полярископа: большое просматриваемое поле позволяет контролировать крупногабаритные заготовки и детали, а также производить одновременный контроль нескольких образцов. Двойное лучепреломление. Все прозрачные кристаллы (кроме кристаллов кубической системы, которые оптически изотропны) обладают способностью двойного лучепреломления, т. е. раздваивания каждого падающего на них светового пучка. Это явление, в 1669 г. впервые обнаруженное датским ученым Э. Бартолином (162S-1698) для исландского шпата (разновидность кальцита СаСО3), объясняется особенностями распространения света в анизотропных средах и непосредственно вытекает из уравнений Максвелла. Если на толстый кристалл исландского шпата направить узкий пучок света, то из кристалла выйдут два пространственно разделенных луча, параллельных друг другу и падающему лучу (рис. 1). Рис. 1 Даже в том случае, когда первичный пучок падает на кристалл нормально, преломленный пучок разделяется на два, причем один из них является продолжением первичного, а второй отклоняется (рис. 2). Второй из этих лучей получил название необыкновенного (е), а первый - обыкновенного (о). Рис. 2 В кристалле исландского шпата имеется единственное направление, вдоль которого двойное лучепреломление не наблюдается. Направление в оптически анизотропном кристалле, по которому луч света распространяется, не испытывая двойного луче преломления, называется оптической осью кристалла. В данном случае речь идет именно о направлении, а не о прямой линии, проходящей через какую-то точку кристалла. Любая прямая, проходящая параллельно данному направлению, является оптической осью кристалла. Кристаллы в зависимости от типа их симметрии бывают одноосные и двуосные, т.е. имеют одну или две оптические оси (к первым и относится исландский шпат). Исследования показывают, что вышедшие из кристалла лучи плоскополяризованы во взаимно перпендикулярных плоскостях. Плоскость, проходящая через направление луча света и оптическую ось кристалла, называется главной плоскостью (или главным сечением кристалла). Колебания светового вектора (вектора напряженности Е электрического поля) в обыкновенном луче происходят перпендикулярно главной плоскости, в необыкновенном - в главной плоскости (рис. 2). Неодинаковое преломление обыкновенного и необыкновенного лучей указывает на различие для них показателей преломления. Очевидно, что при любом направлении обыкновенного луча колебания светового вектора перпендикулярны оптической оси кристалла, поэтому обыкновенный луч распространяется по всем направлениям с одинаковой скоростью и, следовательно, показатель преломления n0для него есть вели чина постоянная. Для необыкновенного же луча угол между направлением колебаний светового вектора и оптической осью отличен от прямого и зависит от направления луча, поэтому необыкновенные лучи распространяются по различным направлениям с разными скоростями. Следовательно, показатель преломления пенеобыкновенного луча является переменной величиной, зависящей от направления луча. Таким образом, обыкновенный луч подчиняется закону преломления (отсюда и название «обыкновенный»), а для необыкновенного луча этот закон не выполняется. После выхода из кристалла, если не принимать во внимание поляризацию во взаимно перпендикулярных плоскостях, эти два луча ничем друг от друга не отличаются. Как уже рассматривалось, обыкновенные лучи распространяются в кристалле по всем направлениям с одинаковой скоростью v0 = c/n0,а необыкновенные - с разной скоростью vв =с/nв. (в зависимости от угла между вектором Е и оптической осью). Для луча, распространяющегося вдоль оптической оси, n0 = ne, v0 = ve т.е. вдоль оптической оси существует только одна скорость распространения света. Различие в ve и vвдля всех направлений, кроме направления оптической оси, и обусловливает явление двойного лучепреломления света в одноосных кристаллах. Допустим, что в точке Sвнутри одноосного кристалла находится точечный источник света. На рис. 3 показано распространение обыкновенного и необыкновенного лучей в кристалле (главная плоскость совпадает с плоскостью чертежа, ОО' - направление оптической оси). Рис. 3 Волновой поверхностью обыкновенного луча (он распространяется с v0 = const) является сфера, необыкновенного луча (ve const) - эллипсоид вращения. Наибольшее расхождение волновых поверхностей обыкновенного и необыкновенного лучей наблюдается в направлении, перпендикулярном оптической оси. Эллипсоид и сфера касаются друг друга в точках их пересечения с оптической осью ОО', Если то ve < vо (nе > no),эллипсоид необыкновенного луча вписан в сферу обыкновенного луча (эллипсоид скоростей вытянут относительно оптической оси) и одноосный кристалл называется положительным (рис. 279, а). Если ve > v0 (ne < n0),то эллипсоид описан вокруг сферы (эллипсоид скоростей растянут в направлении, перпендикулярном оптической оси) и одноосный кристалл называется отрицательным (рис. 3, б). Рассмотренный выше исландский шпат относится к отрицательным кристаллам. Призма Николя Схема действия призмы Николя. Призма Николя (сокр. николь) - поляризационное устройство, в основе принципа действия которого лежат эффекты двойного лучепреломления и полного внутреннего отражения. Устройство изобрёл Уильям Николь в 1820 г. Призма Николя представляет собой две одинаковые треугольные призмы из исландского шпата, склеенные тонким слоем канадского бальзама. Призмы вытачиваются так, чтобы торец был скошен под углом 68° относительно направления проходящего света, а склеиваемые стороны составляли прямой угол с торцами. При этом оптическая ось кристалла (AB) находится под углом 64° с направлением света. Апертура полной поляризации призмы составляет 29°. Особенностью призмы является изменение направления выходящего луча при вращении призмы, обусловенное преломлением скошенных торцов призмы. Призма не может применяться для поляризации ультрафиолета, так как канадский бальзам поглощает ультрафиолет. Принцип действия: Свет с произвольной поляризацией, проходя через торец призмы испытывет двойное лучепреломление, расщепляясь на два луча - обыкновенный, имеющий горизонтальную плоскость поляризации (AO) и необыкновенный, с вертикальной плоскостью поляризации (АE). После чего обыкновенный луч испытывает полное внутреннее отражение о плоскость склеивания и выходит через боковую поверхность. Необыкновенный беспрепятственно выходит через противоположный торец призмы. Применение: Призма Николя находит своё применение наряду с прочими поляризационными устройствами в различных областях науки и техники, хотя подавляющей частью они ныне заменены на более технологичные. До появления дешёвых поляроидных плёнок призма Николя использовалась для просмотра стереофотографий, проецируемых на экран (предложено Андертоном в 1891 г. [1]). Закон Малюса - зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла между плоскостями поляризации падающего света и поляризатора. где I0 - интенсивность падающего на поляризатор света, I - интенсивность света, выходящего из поляризатора. Установлен Э.Л. Малюсом в 1810 году. Свет с иной (не линейной) поляризацией может быть представлен в виде суммы двух линейно-поляризованных составляющих, к каждой из которых применим закон Малюса. По закону Малюса рассчитываются интенсивности проходящего света во всех поляризационных приборах, например в поляризационных фотометрах и спектрофотометрах. Потери на отражение, зависящие от и не учитываемые законом Малюса, определяются дополнительно. Закон Брюстера - закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко установить, что в этом случае отраженный и преломленный лучи взаимно перпендикулярны. Соответствующий угол называется углом Брюстера. Закон Брюстера:, где n12 - показатель преломления второй среды относительно первой,?Br - угол падения (угол Брюстера). Это явление оптики названо по имени шотландского физика Дэвида Брюстера, открывшего его в 1815 году.
11. Явление электромагнитной индукции открыто Фарадеем в 1831 г. При изменении магнитного потока, пронизывающего замкнутый проводящий контур, в нем возникает индукционный ток. Наличие индукционного тока i вызвано появлением в контуре ЭДС индукции
где «-» в этом уравнении связан со знаком магнитного потока и знаком ЭДС индукции (рис. 1, а, б).
Знак магнитного потока связан с выбором нормали
Направление индукционного тока (знак ЭДС индукции) определяется правилом Ленца: Индукционный ток имеет такое направление, что созданное им магнитное поле противодействует причине, его вызывающей. Действительно, индукционный ток в контуре создает собственное магнитное поле, которое препятствует изменению внешнего магнитного потока, вызывающего ЭДС индукции (рис. 2, а, б). Если, например, постоянный магнит приближать северным магнитным полюсом к виткам катушки, замкнутой на гальванометр, то в контуре возникает индукционный ток, такого направления (стрелка гальванометра отклоняется влево), что созданное им магнитное поле будет направлено навстречу нарастающему магнитному потоку, стремясь его уменьшить (рис. 2, а). Если же магнит удалять от катушки северным магнитным полюсом, то возникает индукционный ток противоположного направления (стрелка гальванометра отклоняется вправо) и созданное им магнитное поле будет направлено в сторону убывающего магнитного потока, стремясь замедлить его уменьшение (рис. 2, б). Силовые линии магнитного поля, созданного индукционным током на рис. 2, а, б, показаны в виде пунктирных линий с двойными стрелками. Индукционный ток можно вызвать различными способами. В рассмотренном выше примере контур покоился, его витки пронизывали силовые линии переменного магнитного поля постоянного магнита. В этом случае возникновение индукционного тока свидетельствует о том, что изменяющееся магнитное поле вызывает в контуре появление сторонних сил. Ясно, что это не магнитные силы, т. к. привести в движение покоившиеся заряды (v = 0) они не могут. Других сил, кроме силы Следовательно, индукционный ток вызван появляющимся в проводящем контуре электрическим полем Позднее Максвелл предположил, что изменяющееся во времени магнитное поле приводит к появлению в пространстве переменного электрического поля независимо от того, есть замкнутый контур или нет. Этот контур лишь позволяет обнаружить (по возникновению в нем индукционного тока) существование электрического поля (не путать с электростатическим полем, создаваемым неподвижными зарядами). Циркуляция вектора
Символ частной производной определяет то положение, когда контур и натянутая на него поверхность, находятся в покое. Магнитный поток, пронизывающий этот контур,
Вследствие того, что интегрирование проводится по произвольной поверхности, натянутой на неподвижный контур,
С учетом этого выражение (3.77) представим в виде
или в дифференциальной форме rot Уравнение (4) выражает локальную связь между электрическим и магнитным полями: переменное магнитное поле Поскольку циркуляция переменного электрического поля, возбуждаемого переменным магнитным полем, отлична от нуля, то это электрическое поле не потенциально, а является вихревым, как и магнитное поле. Рассмотрим, что является причиной возникновения индукционного тока, если проводящий контур движется в постоянном магнитном поле (рис. 3) Пусть одна сторона контура АС является подвижной. При перемещении АС, например, вправо со скоростью На каждый электрон начнет действовать вдоль АС сила Лоренца
где v*- скорость упорядоченного движения электронов вдоль проводника под действием составляющей силы Лоренца.
Электроны начнут перемещаться вниз по линии АС - возникнет индукционный ток, направленный вверх. Из-за перераспределения зарядов на поверхности проводящего контура возникнет электрическое поле, которое возбудит ток и в остальных участках проводника. Поэтому напряженность возникшего стороннего электрического поля (v* = 0)
Циркуляция вектора где знак «-» взят в соответствии с правилом правого винта (положительное направление обхода контура - по часовой стрелке). В этом случае стороннее электрическое поле Приращение площади, ограниченной контуром в единицу времени при движении АС, запишем в виде
Поэтому формула (5) принимает вид
где dФm - изменение магнитного потока сквозь контур; ( Закон электромагнитной индукции остается справедливым для контура произвольной формы и размеров, движущегося в неоднородном магнитном поле. Таким образом, возникновение ЭДС индукции при движении контура в неоднородном постоянном магнитном поле объясняется действием силы Лоренца. ЭДС индукции возникает в контуре за счет возбуждения изменяющегося во времени электрического поля или из-за действия силы Лоренца при изменении магнитного потока, пронизывающего контур. Поэтому закон электромагнитной индукции можно представить в общем виде:
Изменяющийся по величине ток всегда создаёт изменяющееся магнитное поле, которое, в свою очередь, всегда индуктирует ЭДС. При всяком изменении тока в катушке (или вообще в проводнике) в ней самой индуктируется ЭДС самоиндукции, она зависит от скорости изменения тока. Чем больше скорость изменения тока, тем больше ЭДС самоиндукции. Величина ЭДС самоиндукции зависит также от числа витков катушки и её размеров. Чем больше диаметр катушки и число её витков, тем больше ЭДС самоиндукции. Эта зависимость имеет большое значение в электротехнике. Направление ЭДС самоиндукции определяет Закон Ленца:
ЭДС самоиндукции имеет всегда такое направление, при котором она препятствует изменению вызвавшего её тока.
Иначе говоря, убывание тока в катушке влечёт за собой появление ЭДС самоиндукции, направленной по направлению тока, т. е. препятствующей его убыванию. И, наоборот, - при возрастании тока в катушке возникает ЭДС самоиндукции, направленная против тока, т. е. препятствующая его возрастанию. Если ток в катушке не изменяется, то никакой ЭДС самоиндукции не возникает. Явление самоиндукции особенно резко проявляется в цепи, содержащей в себе катушку со стальным сердечником, так как сталь значительно увеличивает магнитный поток катушки, а следовательно, и величину ЭДС самоиндукции. Продемонстрировать явление самоиндукции можно, проведя следующий эксперимент. Соберём электрическую цепь, состоящую из аккумулятора, разъединителя и двух параллельных цепей: в первой - лампочка и резистор, а во второй - лампочка и катушка, причём сопротивление обеих лампочек одинаковое, и сопротивление резистора и катушки также одинаково. 1. При включении разъединителя лампа Л1 загорится с задержкой, так как ЭДС самоиндукции катушки препятствует быстрому нарастанию тока в цепи лампы Л1 (рис. 1а и 1б). 2. При отключении разъединителя обе лампы кратковременно вспыхнут, так как ЭДС самоиндукции катушки выше ЭДС батареи. Когда ЭДС самоиндукции иссякает, то обе лампы одновременно гаснут (рис. 2а и 2б).
· Проводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока. Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля. · Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток Ф =LI, причем при изменении тока на d I магнитный поток изменяется на dФ= L d I. Однако для изменения магнитного потока на величину dФ необходимо совершить работу d А=I dФ =LI d I. Тогда работа по созданию магнитного потока Ф будет равна · Следовательно, энергия магнитного поля, связанного с контуром, W = LI2/2 (130.1) · Исследование свойств переменных магнитных полей, в частности распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля локализована в пространстве. Это соответствует представлениям теории поля. · Энергию магнитного поля можно представить как функцию величин, характеризующих это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение · · Так как I=Bl/ (m 0 mN) и В=m 0 mH, то · · Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью · · Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный объемной плотности энергии электростатического поля, с той разницей, что электрические величины заменены в нем магнитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднородных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам.
12. Интерфере́нция све́та — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.
Впервые явление интерференции было независимо обнаружено Робертом Бойлем (1627—1691 гг.) и Робертом Гуком (1635—1703 гг.). Они наблюдали возникновение разноцветной окраски тонких плёнок (интерференционных полос), подобных масляным или бензиновым пятнам на поверхности воды. В 1801 году Томас Юнг (1773—1829 гг.), введя «принцип суперпозиции», первым объяснил явление интерференции света, ввёл в научный обиход термин «интерференция» (1803) и объяснил «цветастость» тонких пленок. Он также выполнил первый демонстрационный эксперимент по наблюдению интерференции света, получив интерференцию от двух щелевых источников света (1802); позднее этот опыт Юнга стал классическим. Интерферометр — измерительный прибор, действие которого основано на явлении интерференции. Принцип действия интерферометра заключается в следующем: пучок электромагнитного излучения (света, радиоволн и т. п.) с помощью того или иного устройства пространственно разделяется на два или большее количество когерентных пучков. Каждый из пучков проходит различные оптические пути и направляется на экран, создавая интерференционную картину, по которой можно установить разность фаз интерферирующих пучков в данной точке картины. Интерферометры применяются как при точных измерениях длин, в частности в станко- и машиностроении, так и для оценки качества оптических поверхностей и проверки оптических систем в целом.
13. Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос. Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т. Юнгом. Независимо от него в 1818 г. французский ученый О. Френель развил количественную теорию дифракционных явлений. В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Принцип Гюйгенса в его первоначальном виде позволял находить только положения волновых фронтов в последующие моменты времени, т. е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающей вторичных волн Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 3.8.1 иллюстрирует принцип Гюйгенса–Френеля.
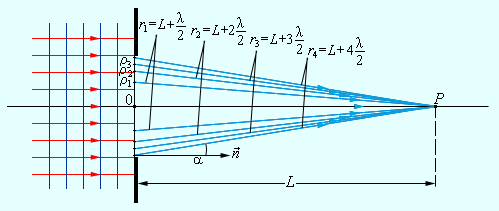
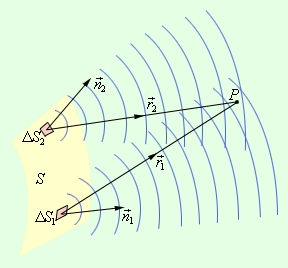
Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер. Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS1, ΔS2 и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием. Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса R в непрозрачном экране (рис. 3.8.2).
Точка наблюдения P находится на оси симметрии на расстоянии L от экрана. В соответствии с принципом Гюйгенса–Френеля следует мысленно заселить волновую поверхность, совпадающую с плоскостью отверстия, вторичными источниками, волны от которых достигают точки P. В результате интерференции вторичных волн в точке P возникает некоторое результирующее колебание, квадрат амплитуды которого (интенсивность) нужно определить при заданных значениях длины волны λ, амплитуды A0 падающей волны и геометрии задачи. Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на половину длины волны, т. е.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.190.187 (0.016 с.) |

 i. При этом ЭДС индукции не зависит от того, каким образом происходит изменение магнитного потока, а определяется лишь скоростью его изменения
i. При этом ЭДС индукции не зависит от того, каким образом происходит изменение магнитного потока, а определяется лишь скоростью его изменения 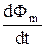 . Закон электромагнитной индукции записывают в виде
. Закон электромагнитной индукции записывают в виде , (1)
, (1) Рис. 1
Рис. 1
 к поверхности S, ограниченной рассматриваемым контуром. Знак ЭДС индукции - с выбором положительного направления обхода по контуру. Направление нормали
к поверхности S, ограниченной рассматриваемым контуром. Знак ЭДС индукции - с выбором положительного направления обхода по контуру. Направление нормали  i и
i и  Рис. 2
Рис. 2
 , нет.
, нет. . Это поле и вызывает появление ЭДС индукции в неподвижном контуре.
. Это поле и вызывает появление ЭДС индукции в неподвижном контуре. =
= 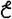 i ¹ 0. (2)
i ¹ 0. (2) .
. .
. (3)
(3)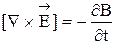 . (4)
. (4) в данной точке определяет ротор поля
в данной точке определяет ротор поля  электроны проводимости начнут двигаться с такой же скоростью.
электроны проводимости начнут двигаться с такой же скоростью. ,
, Рис. 3
Рис. 3

 , (5)
, (5)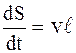 .
. , (6)
, (6) .
. Явление самоиндукции имеет как положительные, так и отрицательные свойства, причём и те и другие проявляются при работе аппаратов и электрических цепей подвижного состава метрополитена:
Явление самоиндукции имеет как положительные, так и отрицательные свойства, причём и те и другие проявляются при работе аппаратов и электрических цепей подвижного состава метрополитена:
 , получим
, получим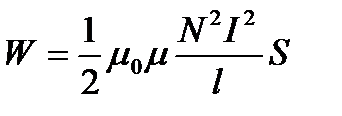
 , где Sl = V — объем соленоида. (130.2)
, где Sl = V — объем соленоида. (130.2) (130.3)
(130.3)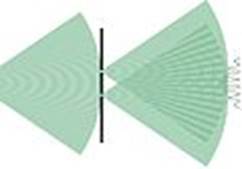
 и
и  – нормали
– нормали