
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное поле кругового витка с током.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Общая картина силовых линий тоже просматривается (рис.7.10). Сложение гармонических колебаний Если система участвует одновременно в нескольких колебательных процессах, то под сложением колебаний понимают нахождение закона, описывающий результиующий колебательный процесс.
Направление вектора Мы добыли такой результат:
А теперь, в качестве проверки, поле в центре витка равна: 39. Работа, совершаемая при перемещении контура с током в магнитном поле. Рассмотрим отрезок проводника с током, способный свободно перемещаться по двум направляющим во внешнем магнитном поле (рис.9.5). Магнитное поле будем считать однородным и направленным под углом α по отношению к нормали к плоскости переме-щения проводника.
Рис.9.5. Отрезок проводника с током в однородном магнитном поле. Как видно из рис.9.5, вектор
где I – сила тока в проводнике; l – длина проводника; B – индукция магнитного поля. Работа этой силы на элементарном пути перемещения ds есть:
Произведение lds равно площади dS, заметанной проводником при движении, а величина BdScosα равна потоку магнитной индукции dФ через эту площадь. Следовательно, можем написать: dA=IdФ. Рассматривая отрезок проводника с током как часть замкнутого контура и интегрируя это соотношение, найдем работу при перемещении контура с током в магнитном поле: A = I(Ф2 – Ф1) где Ф1 и Ф2 обозначают поток индукции магнитного поля через площадь контура соответственно в начальном и конечном положениях. 40. Движение заряженных частиц в Однородном магнитном поле Рассмотрим частный случай, когда нет электрического поля, но имеется магнитное поле. Предположим, что частица, обладающая начальной скоростью u0, попадает в магнитное поле с индукцией B. Это поле мы будем считать однородным и направленным перпендикулярно к скорости u0.
Основные особенности движения в этом случае можно выяснить, не прибегал к полному решению уравнений движения. Прежде всего, отметим, что действующая на частицу сила Лоренца всегда перпендикулярна к скорости движения частицы. Это значит, что работа силы Лоренца всегда равна нулю; следовательно, абсолютное значение скорости движения частицы, а значит, и энергия частицы остаются постоянными при движении. Так как скорость частицы u не изменяется, то величина силы Лоренца
остается постоянной. Эта сила, будучи перпендикулярной, к направлению движения, является центростремительной силой. Но движение под действием постоянной по величине центростремительной силы есть движение по окружности. Радиус r этой окружности определяется условием
откуда
Если энергия электрона выражена в эВ и равна U, то
и поэтому
Кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: время полного обращения частицы по окружности (период движения) не зависит от энергии частицы. Действительно, период обращения равен
Подставляя сюда вместо r его выражение по формуле (3.6), имеем:
Частота же оказывается равной
Для данного типа частиц и период, и частота зависят только от индукции магнитного поля. Выше мы предполагали, что направление начальной скорости перпендикулярно к направлению магнитного поля. Нетрудно сообразить, какой характер будет иметь движение, если начальная скорость частицы составляет некоторый угол с направлением поля.
В результате сложения обоих движений частица будет двигаться по цилиндрической спирали. Шаг винта этой спирали равен
подставляя вместо T его выражение (3.7), имеем:
41. Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота. Свойства В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов
Скорость электронов
где
Коэффициент
42. Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа[ источник не указан 111 дней ] 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током. 43.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 943; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.188.174 (0.007 с.) |











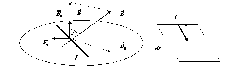
 По идее, нас интересовало бы поле
По идее, нас интересовало бы поле  , но в элементарных функциях указать поле этого витка нельзя. Найти можно только на оси симметрии. Мы ищем поле в точках (х,0,0).
, но в элементарных функциях указать поле этого витка нельзя. Найти можно только на оси симметрии. Мы ищем поле в точках (х,0,0).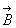 определяется векторным произведением
определяется векторным произведением 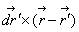 . Вектор
. Вектор  и
и  . Когда мы начнём суммировать эти вектора, то все перпендикулярные составляющие в сумме дадут ноль.
. Когда мы начнём суммировать эти вектора, то все перпендикулярные составляющие в сумме дадут ноль.  . А теперь пишем:
. А теперь пишем:  ,
,  =
=  , а
, а  .
.  , и, наконец1),
, и, наконец1),  .
.
 .
.
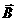 имеет две составляющие
имеет две составляющие  и
и  , из которых только составляющая
, из которых только составляющая 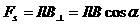 ,
, .
.



 (3.6)
(3.6)

 (3.7)
(3.7)
 В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Ut, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью
В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Ut, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью


 течёт электрический ток под действиемнапряжённости
течёт электрический ток под действиемнапряжённости  . Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.
. Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде. не скомпенсирует магнитную составляющую силы Лоренца:
не скомпенсирует магнитную составляющую силы Лоренца:
 можно выразить через плотность тока:
можно выразить через плотность тока:
 — концентрация носителей заряда. Тогда
— концентрация носителей заряда. Тогда
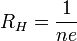 пропорциональности между
пропорциональности между  называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак
называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак  , что объясняется в полуклассической и квантовой теориях твёрдого тела.
, что объясняется в полуклассической и квантовой теориях твёрдого тела.


