
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Циркуляция вектора магнитной индукции.Расчёт магнитного поля длинного соленоида.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Циркуляция Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта, а ток противоположного направления - отрицательным (рис. 7, где I1 > 0, I3 > 0, I2 < 0, I4 < 0).
Рассмотрим магнитное поле прямого проводника с током бесконечной длины (рис.8, ток направлен к нам). В качестве замкнутой поверхности используем окружность L радиуса r. Вектор индукции магнитного поля
Согласно определению циркуляции вектора
Формулу (27) называют законом полного тока. Если ток распределен по объему, где расположен контур L, то
Интеграл берется по произвольной поверхности S, натянутой на контур L. Поэтому плотность тока
Замечание 1: Магнитное поле называют вихревым, или соленоидальным, поскольку циркуляция вектора
Следовательно,
Для электростатического поля мы вводили понятие циркуляции вектора напряжённости электростатического поля как
Полученное выражение называется законом полного тока для магнитного поля в вакууме и читается так: циркуляция вектора магнитной индукции в вакууме по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром, умноженной на магнитную постоянную.Напомним, что для электростатического поля циркуляция вектора напряжённости равна нулю и это позволило ввести понятие потенциала для электростатического поля. Для магнитного поля циркуляция отлична от нуля и это означает, что для магнитного поля нельзя ввести понятие потенциала. Если токи текут по всему пространству, охватываемому контуром, то
37.Действие магнитного поля на движущийся заряд.Характер движения свободного заряда в магнитном поле. Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника. Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца. Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:
38.Элементарная теория Холла(на примере проводника). Эффект Холла – появление в проводнике (или в полупроводнике) с током плотностью , (1) где R – коэффициент пропорциональности (коэффициент Холла), его величина и знак зависит от химического состава проводника, от температуры и заряда носителей тока; I – сила тока в образце; В – индукция магнитного тока; d – толщина образца. Рассмотрим элементарную теорию эффекта Холла. Пусть носителями тока являются электроны (например, в металлах и примесных полупроводниках n-типа). При протекании в образце тока плотностьюэлектроны имеют скорость дрейфа
В Fэл = Fл или еЕу = еvВ, (3) так как в данном случае вектор скорости Из уравнения (3) находим напряженность поля Холла: Еу =vВ(4) и разность потенциалов между гранями 1 и 2 (напряжение Холла):
где b– размер образца вдоль направления поля Холла. Учитывая, что плотность тока j=еnv, гдеn– концентрация электронов проводимости в образце, а сила тока через образецI=jS, гдеS=bd– площадь сечения пластинки, получим для скорости движения электронов выражение:
Напряжение Холла, согласно уравнению (5) с учетом формулы (6), запишем в виде
Сравнив выражения (1) и (7), получим Коэффициент Холла (м3/Кл):
Более строгая теория, учитывающая взаимодействия носителей тока (электронов) с кристаллической решеткой, дает постоянную Холла:
где r– Холл-фактор, его величинаr1 и зависит от напряженности магнитного поля, температуры и свойств материала образца. Для слабо легированного германия при комнатной температуре>r/8.p=3Из формулы (8) следует, что знак коэффициента Холла определяется знаком заряда носителей тока. Для металлов и полупроводников n-типа величинаR0, а для полупроводников с дырочной проводимостью (р-типа)<R0.>Знак напряжения Холла связан со знаком носителей тока в образце. Величина постоянной Холла, которая может быть определена из опыта, связана с концентрацией и подвижностью носителей тока (9). Таким образом, эффект Холла может быть применен для определения этих параметров (знака, концентрации и подвижности носителей тока), что особенно важно в теории и практике применения полупроводниковых материалов. Очевидно, знание этих параметров для какого-либо образца позволяет применить его в качестве датчика величины магнитного поля, кроме того, эффект Холла при некоторых условиях применим для определения плотности тока в образце.Эффект Холла технологически является очень выгодным, на нем основан принцип работы МГД - генераторов, преобразующих тепловую энергию непосредственно в электрическую. Также на основе эффекта Холла работают некоторые виды ионных реактивных двигателей.Эффект Холла лежит в основе одной из самых прогрессивных технологий бесконтактной регистрации положения, перемещения, скорости вращения и присутствия ферромагнитных объектов. Основным чувствительным элементом таких устройств является датчик Холла, который представляет собой тонкую прямоугольную пластину (площадь – несколько мм2), или пленку, изготовленную из полупроводникового материала в котором эффект Холла проявляется в сильной степени (германий Ge, кремний Si, антимонид и арсенид индия InSb и InAs, арсенид-фосфид индия InAsP, арсенид галлия GaAs, селенид и теллурид ртути HgSe и HgTe). Пластина имеет четыре электрода для подвода тока и съёма напряжения Холла. Чтобы избежать механических повреждений, пластинку монтируют (а пленку напыляют в вакууме) на прочной подложке из диэлектрика (слюды, керамики). Для получения наибольшего эффекта толщина пластины (плёнки) делается как можно меньшей.Благодаря тому, что выходной эффект определяется произведением двух величин (НиI), датчики Холла имеют весьма широкое применение.Датчики Холла применяют для бесконтактного измерения магнитных полей (от 10-5 до 106 А/м).
|
||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.107.152 (0.008 с.) |

 по произвольному контуру L в вакууме равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охваченных этим контуром.
по произвольному контуру L в вакууме равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охваченных этим контуром. Рис.7.
Рис.7.
 перпендикулярен радиус-вектору
перпендикулярен радиус-вектору  и совпадает по направлению с вектором элемента длины
и совпадает по направлению с вектором элемента длины  .
. Рис. 8
Рис. 8
 имеем
имеем , (cosa =1)Применив формулу индукции прямого проводника с током бесконечной длины, последнее равенство перепишем в виде
, (cosa =1)Применив формулу индукции прямого проводника с током бесконечной длины, последнее равенство перепишем в виде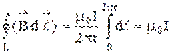 .Теорема остается справедливой и для контура произвольной формы, который охватывает N проводников с током, т. е.
.Теорема остается справедливой и для контура произвольной формы, который охватывает N проводников с током, т. е.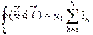 . (27)
. (27) .
. под интегралом соответствует точке, где расположена площадка (направление обхода и вектор нормали
под интегралом соответствует точке, где расположена площадка (направление обхода и вектор нормали 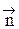 связаны правилом правого винта). С учетом этого теорему о циркуляции запишем в виде
связаны правилом правого винта). С учетом этого теорему о циркуляции запишем в виде . (28)
. (28) не равна нулю (в отличие от электростатического поля, которое является потенциальным).Замечание 2: Поле вектора
не равна нулю (в отличие от электростатического поля, которое является потенциальным).Замечание 2: Поле вектора  к площадке S, натянутой на контур L. Ориентация этого контура связана с вектором нормали
к площадке S, натянутой на контур L. Ориентация этого контура связана с вектором нормали  к плоскости контура правилом правого винта. В пределе при S ® 0, имеем
к плоскости контура правилом правого винта. В пределе при S ® 0, имеем . (29)Формулу (29) называют ротором поля
. (29)Формулу (29) называют ротором поля  на нормаль. Используя (29), формулу (28) представим в виде:
на нормаль. Используя (29), формулу (28) представим в виде:  (30)или
(30)или  (31)где
(31)где  - векторный дифференциальный оператор.
- векторный дифференциальный оператор. . (32).Ротор поля
. (32).Ротор поля 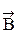 совпадает по направлению с вектором плотности тока
совпадает по направлению с вектором плотности тока  в данной точке. Формула (32) - дифференциальная форма теоремы о циркуляции
в данной точке. Формула (32) - дифференциальная форма теоремы о циркуляции  . Дифференциальная форма теоремы о циркуляции
. Дифференциальная форма теоремы о циркуляции  расширяет ее возможности для исследования и расчета сложных магнитных полей.
расширяет ее возможности для исследования и расчета сложных магнитных полей. . (3.16)Аналогично вводится циркуляция для магнитного поля:
. (3.16)Аналогично вводится циркуляция для магнитного поля:  . (3.17)
. (3.17) Здесь Вl=Bcosa – проекция вектора B на направление касательной к контуру, a – угол между касательной к контуру и вектором B. Посчитаем теперь циркуляцию для прямолинейного проводника с током. В качестве контура обхода выберем окружность некоторого радиуса b, в центре которой находится проводник с током. В этом случае индукция определяется выражением (3.14). Теперь, с учётом выражения (3.14), посчитаем циркуляцию (3.17). Как видно из рис. 3.7, dl=bda. Тогда
Здесь Вl=Bcosa – проекция вектора B на направление касательной к контуру, a – угол между касательной к контуру и вектором B. Посчитаем теперь циркуляцию для прямолинейного проводника с током. В качестве контура обхода выберем окружность некоторого радиуса b, в центре которой находится проводник с током. В этом случае индукция определяется выражением (3.14). Теперь, с учётом выражения (3.14), посчитаем циркуляцию (3.17). Как видно из рис. 3.7, dl=bda. Тогда (3.18)При вычислении интеграла мы также учли, что cosa=1. Мы получили этот результат, специальным образом выбрав контур обхода. Оказывается, этот результат остаётся справедливым для любого контура обхода. Знак уравнения (3.18) зависит только от направления обхода – если направление обхода и направление тока соответствуют правилу правого винта, то знак уравнения (3.18) будет положительным. В противном случае знак будет отрицательным. Если же контур обхода охватывает несколько токов, то, в силу принципа суперпозиции для магнитного поля, можно записать, что
(3.18)При вычислении интеграла мы также учли, что cosa=1. Мы получили этот результат, специальным образом выбрав контур обхода. Оказывается, этот результат остаётся справедливым для любого контура обхода. Знак уравнения (3.18) зависит только от направления обхода – если направление обхода и направление тока соответствуют правилу правого винта, то знак уравнения (3.18) будет положительным. В противном случае знак будет отрицательным. Если же контур обхода охватывает несколько токов, то, в силу принципа суперпозиции для магнитного поля, можно записать, что . (3.19)Каждый из интегралов в последней сумме равен m0Im. Таким образом, окончательно получим
. (3.19)Каждый из интегралов в последней сумме равен m0Im. Таким образом, окончательно получим  . (3.20)
. (3.20) , и тогда вместо уравнения (3.20) получим
, и тогда вместо уравнения (3.20) получим  . (3.21)Преобразуем левую часть уравнения (3.21) по теореме Стокса:
. (3.21)Преобразуем левую часть уравнения (3.21) по теореме Стокса: . (3.22)Последнее равенство в выражении (3.22) справедливо, если подинтегральные выражения одинаковы в каждой точке поверхности S:
. (3.22)Последнее равенство в выражении (3.22) справедливо, если подинтегральные выражения одинаковы в каждой точке поверхности S:  . (3.23)Поля, у которых ротор отличен от нуля, называются вихревыми или соленоидальными. Таким образом, магнитное поле является вихревым.Применим закон полного тока для расчёта магнитного поля бесконечно длинного соленоида (соленоидом называют катушку с намотанным на ней проводом, по которому пропускают электрический ток). Соленоиды используют для получения магнитного поля. В реальности, модель бесконечно длинного соленоида можно использовать для реальных соленоидов, если длина соленоида много больше его диаметра. Эксперимент показывает, что магнитное поле, в основном, сосредоточено внутри соленоида. Выберем некий контур обхода АБСД (рис.3.8) и посчитаем циркуляцию вектора магнитной индукции для этого контура.Пусть на длине AD=BC укладывается N витков. Тогда
. (3.23)Поля, у которых ротор отличен от нуля, называются вихревыми или соленоидальными. Таким образом, магнитное поле является вихревым.Применим закон полного тока для расчёта магнитного поля бесконечно длинного соленоида (соленоидом называют катушку с намотанным на ней проводом, по которому пропускают электрический ток). Соленоиды используют для получения магнитного поля. В реальности, модель бесконечно длинного соленоида можно использовать для реальных соленоидов, если длина соленоида много больше его диаметра. Эксперимент показывает, что магнитное поле, в основном, сосредоточено внутри соленоида. Выберем некий контур обхода АБСД (рис.3.8) и посчитаем циркуляцию вектора магнитной индукции для этого контура.Пусть на длине AD=BC укладывается N витков. Тогда . (3.24)
. (3.24)  Интегралы на участках АВ и СD равны нулю, поскольку на этих участках Bl=0 (угол между векторами B и dl равен 90o). На участке DA магнитное поле равно нулю (для конечного соленоида поле вне его, конечно же, будет, но очень слабым, поэтому им можно пренебречь). Таким образом, вместо выражения (3.24) получим
Интегралы на участках АВ и СD равны нулю, поскольку на этих участках Bl=0 (угол между векторами B и dl равен 90o). На участке DA магнитное поле равно нулю (для конечного соленоида поле вне его, конечно же, будет, но очень слабым, поэтому им можно пренебречь). Таким образом, вместо выражения (3.24) получим . (3.25)Теперь вспомним, что поле внутри соленоида постоянное и его можно вынести за знак интеграла. Оставшийся интеграл даст длину участка ВС=l. Следовательно, для поля внутри соленоида окончательно получим
. (3.25)Теперь вспомним, что поле внутри соленоида постоянное и его можно вынести за знак интеграла. Оставшийся интеграл даст длину участка ВС=l. Следовательно, для поля внутри соленоида окончательно получим  . (3.26)Здесь n = N/l – число витков, приходящееся на единицу длины. Важное место в технике занимает также тороид – кольцевая катушка с навитым на ней проводом. Как показывает опыт, поле полностью сосредоточено внутри катушки, поэтому выберем контур обхода, проходящий внутри катушки. Очевидно, что это будет окружность радиуса r. Если в катушке N витков, то для поля внутри тороида получим
. (3.26)Здесь n = N/l – число витков, приходящееся на единицу длины. Важное место в технике занимает также тороид – кольцевая катушка с навитым на ней проводом. Как показывает опыт, поле полностью сосредоточено внутри катушки, поэтому выберем контур обхода, проходящий внутри катушки. Очевидно, что это будет окружность радиуса r. Если в катушке N витков, то для поля внутри тороида получим  . (3.27)Из выражений (3.26) и (3.27) видно, что формулы для тороида и бесконечно длинного соленоида одинаковы. И это неудивительно, если вспомнить, что бесконечно длинный соленоид можно представить как тороид с бесконечно большими радиусами.
. (3.27)Из выражений (3.26) и (3.27) видно, что формулы для тороида и бесконечно длинного соленоида одинаковы. И это неудивительно, если вспомнить, что бесконечно длинный соленоид можно представить как тороид с бесконечно большими радиусами. .Сила Ампера равна
.Сила Ампера равна  , сила тока равна
, сила тока равна 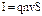 (см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:
(см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим: ,где
,где  - угол между векторами скорости и магнитной индукции. Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону). Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
- угол между векторами скорости и магнитной индукции. Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону). Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы. , помещенном в магнитное поле
, помещенном в магнитное поле  , напряжения U в направлении, перпендикулярном векторам и. Эффект был открыт в 1879 г. американским физиком Эдвином Гербертом Холлом.Холл экспериментально установил следующее выражение для напряжения, впоследствии названное напряжением Холла или Холловской разностью потенциалов:
, напряжения U в направлении, перпендикулярном векторам и. Эффект был открыт в 1879 г. американским физиком Эдвином Гербертом Холлом.Холл экспериментально установил следующее выражение для напряжения, впоследствии названное напряжением Холла или Холловской разностью потенциалов: 
 (рис.1). Если проводник с током помещен в магнитное поле, то на электроны действует сила Лоренца:
(рис.1). Если проводник с током помещен в магнитное поле, то на электроны действует сила Лоренца: , (2)
, (2)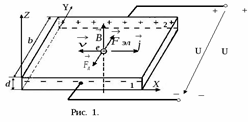 заряд. Это приводит к появлению поперечного электрического поля
заряд. Это приводит к появлению поперечного электрического поля  , направленного вдоль осиY, и действующего на электроны с силой
, направленного вдоль осиY, и действующего на электроны с силой 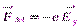 , направление которой противоположно силе Лоренца. Когда напряженность поперечного поляЕу достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Этому состоянию соответствует условие
, направление которой противоположно силе Лоренца. Когда напряженность поперечного поляЕу достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Этому состоянию соответствует условие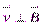 .
.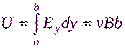 , (5)
, (5) . (6)
. (6) (7)
(7)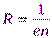 (8)
(8) (9)
(9)


