
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение вектора магнитной индукции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Магни́тная инду́кция
где α — угол между векторами скорости и магнитной индукции. 70) Теорема Гаусса для магнитного поля. Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
71) Почему поток вектора магнитной индукции через замкнутую поверхность равен 0? Потому что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле. 72) Что такое циркуляция вектора напряжённости электростатического поля и чему она равна? Циркуляцией вектора 73) Что такое циркуляция вектора индукции магнитного поля и чему она равна в отсутствии переменного электрического поля? циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную. 74) В чём заключается явление электромагнитной индукции? Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина э.д.с. не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле.
75) Закон Электромагнитной индукции Фарадея. (Э.Д.С. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.) что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина э.д.с. не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой э.д.с., называется индукционным током. 76) Правило Ленца, определяющее направление индукционного тока. Правило Ленца, правило для определения направления индукционного тока: Индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшего этот ток. Сформулировано в 1833 г. Э. Х. Ленцем.Если ток увеличивается, то и магнитный поток увеличивается. Чему равно электродвижущая сила электромагнитной индукции? 78) В чём заключается явление самоиндукции? Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении тока, протекающего через контур. 79) Что называется индуктивностью и от чего она зависит? Индукти́вность — коэффициент пропорциональности между магнитным потоком (создаваемым током какого-либо витка при отсутствии намагничивающих сред, например, в воздухе) и величиной этого тока. Индуктивность зависит только от геометрических свойств контура.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.106 (0.006 с.) |

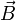 — векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Показывает, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Показывает, с какой силой  магнитное поле действует на заряд
магнитное поле действует на заряд  , движущийся со скоростью
, движущийся со скоростью  .Более точно,
.Более точно,  , равна
, равна
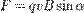
 Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является вихревым.
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является вихревым. по замкнутому контуру
по замкнутому контуру  называют интеграл вида:
называют интеграл вида:  , где d
, где d  – элемент контура (траектории перемещения заряда –замкнутой линии, проведенной в электрическом поле). Циркуляция вектора напряженности по любому замкнутому контуру в электростатическом поле равна нулю.
– элемент контура (траектории перемещения заряда –замкнутой линии, проведенной в электрическом поле). Циркуляция вектора напряженности по любому замкнутому контуру в электростатическом поле равна нулю.


