
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение напряжённости магнитного поля ЗемлиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
С ПОМОЩЬЮ ИНДУКТОРА 1. Цель работы: Ознакомиться с основными характеристиками магнитного поля, законами электромагнетизма. Определить напряженность магнитного поля земли.
Теоретическая часть Конфигурацию магнитных полей принято изображать с помощью силовых линий, касательные к которым совпадают с основной характеристикой поля- вектора магнитной индукции
Рис.1 Около магнитных полюсов силовые линии перпендикулярны к горизонтальной плоскости; во всех других широтах между экватором и полюсами силовые линии Земли составляют с горизонтальной плоскостью угол φ,называемый углом наклонения. Если магнитную стрелку укрепить на горизонтальной оси, перпендикулярной плоскости магнитного меридиана, то очевидно, магнитная стрелка под действием магнитного поля Земли установится в плоскости магнитного меридиана вдоль магнитных силовых линий земного магнетизма, отклонившись от горизонтальной плоскости на угол φ. Основной характеристикой магнитного поля является вектор магнитной индукции
Элементом тока называется вектор, равный по величине произведению малого участка длины dℓпроводника на силу токаJ1в нем и направлен вдоль этого тока. Опыт показывает, что наибольшее отношение (1) достигает при взаимно перпендикулярном расположении векторов Для характеристики магнитного поля без учета взаимодействия его со средой вводится понятие вектора напряженности магнитного поля
где μо = 1.26·-6Гн/м – магнитная постоянная, μ – магнитная проницаемость, характеризующая среду. В СИ напряженность магнитного поля измеряется в А/м. Напряженность
Н2 = Н Следовательно, зная горизонтальную и вертикальную составляющие магнитного поля Земли, легко вычислить и её полную напряженность. Нахождение горизонтальной и вертикальной составляющих напряженности магнитного поля земного магнетизма можно произвести с помощью специальной установки, основными частями которой является индуктор и баллистический гальванометр.
УСТРОЙСТВО ИНДУКТОРА Индуктор состоит из двух легких колец А и В (рис. 2).
Рис. 2 Кольцо А можно поворачивать за головку С на стойке Д около вертикальной оси. Кольцо В можно поворачивать за головку Е около горизонтальной оси. По ободу кольца В уложено 100 витков тонкой изолированной проволоки, концы которой приведены к клеммам К. На основании индуктора укреплен компас для ориентировки плоскости кольца А перпендикулярно или параллельно направлению магнитных силовых линий Земли.
БАЛЛИСТИЧЕСКИЙ ГАЛЬВАНОМЕТР И ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЕГО ИСПОЛЬЗОВАНИЯ
Баллистический гальванометр отличается от обыкновенного тем, что с его помощью можно измерить количество электричества Q, протекающего через него за малый промежуток времени. Подвижная система баллистического, как и любого другого, гальванометра состоит из вращающейся рамки, помещенной между полюсами постоянного магнита. Отличие заключено в конструкции этой подвижной системы. Она сделана таким образом, чтобы период собственных её колебаний был большим по сравнению с длительностью проходящего через него тока. Поэтому кратковременный ток вызывает резкий поворот рамки на угол α, величина которого зависит от длительности и силы этого тока, а значит и от количества прошедшего электричества Q.Поворот рамки вызывает соответствующий ему по величине и направлению отброс «светового зайчика» или смещение индикаторной шкалы с последующим медленным возвращением к нулевому положению. Пусть по рамке баллистического гальванометра протекает ток iГ.Тогда на рамку будет действовать момент силы: М = ВГ РГ, (4) где ВГ – индукция магнитного поля, создаваемого постоянным магнитом галь- ванометра; РГ – магнитный момент рамки с током. По определению РГ = Ѕг iГ nГ, (5) где Ѕг – площадь, ограниченная контуром рамки гальванометра; nГ - число витков на этой рамке. Следовательно, М= ВГ Ѕг iГ nГ (6) Так как величины ВГ,Ѕг, nГ для данного гальванометра являются постоянными, то (6) можно представить в следующем виде: М = С1 iГ, (7) где С 1 = ВГ Ѕг nГ . Запишем основной закон динамики вращения для подвижной системы гальванометра:
где J – момент инерции гальванометра; Δω – изменение угловой скорости поворота рамки за время Δt. Приравнивая левые части формул (7) и (8), получим:
или JΔω = С1 iГ Δt Ввиду того, что в начальный момент рамка покоилась, то есть начальная угловая скорость равнялась нулю, то Δω= ωо, где ωо – угловая скорость, которую получила рамка после прохождения импульса тока. Ввиду того, что Q= i Δt, (10) уравнение (9) можно записать в виде:
Jωо = С1Q, отсюда
Под влиянием приобретенной угловой скорости подвижная система гальванометра повернется на некоторый угол α.Подсчитаем этот угол, исходя из закона сохранения энергии, который для рамки гальванометра запишется следующим образом:
где ķ – коэффициент упругости пружины, возвращающей рамку гальванометра в первоначальное положение. Из (12) выражаем α: α = ωо Учитывая (11), получаем:
Следовательно, Q=С α, (14) где С = Для определения постоянной баллистического гальванометра на практике можно воспользоваться двумя соленоидами. Один соленоид – первичный или нормальный, представляет из себя длинную катушку, последовательно соединенную с аккумулятором, амперметром и реостатом. Другой соленоид – вторичный или баллистический – короткая катушка, одетая на середину первичного соленоида и последовательно соединенная с баллистическим гальванометром. Обозначим параметры этих катушек: площади сечения, линии вдоль оси, количество витков, соответственно Ѕ1 и Ѕ2, ℓ1 и ℓ2 , N1 и N2. Площади поперечных сечений обеих катушек можно считать приблизительно одинаковыми, то есть Ѕ1 = Ѕ2= Ѕ. При включении или выключении тока в цепи с аккумулятором в первичном соленоиде возникает изменяющееся магнитное поле, которое одновременно пронизывает и вторичный соленоид. По закону Фарадея в последнем возникает ЭДС(ε2)электромагнитной индукции:
где ΔФ = Ф2 – Ф1, Ф1 и Ф2 – магнитные потоки, пронизывающие площади Ѕ поперечных сечений катушек в моменты времени, соответствующие t1 и t2, Δt = t2 – t1. Магнитный поток, по определению, равен: Ф = В Ѕсоs θ, (16) где θ – угол между Индуцированная во вторичной катушке ε2 (15) вызывает в ней по закону Ома ток i2:
где R2 – сопротивление всей замкнутой цепи, включающей баллистический гальванометр. Величину R2 мы вычислять не будем, так как в дальнейшем (см. формулы 29 и 30) ее значение сокращается. Учитывая определение количества электричества (10), выражение (17) перепишем в виде:
При включении тока в цепи с первичным соленоидом Ф1 = 0 так как в начальный момент поля нет, при включении, в связи с исчезновением магнитного поля Ф2 = 0. Знак «-» в формуле (18) указывает на направление движения заряда Q во вторичном соленоиде. Поэтому при вычислении его величины этот знак можно опустить. Тогда, обозначая отличный от нуля магнитный поток Ф1 или Ф2 через Ф и учитывая, что угол
Для вычисления Ф в соответствии с формулой (16) необходимо определить Н = i1n1, (20) где i1- ток, текущий в первичном соленоиде,
Тогда, подставляя выражение для Ф (16), В (2), Н (20) в формулу (19), получим:
Однако значение Q также связано с величиной поворота рамки гальванометра (14). Приравнивая правые части соотношений (14) и (21), имеем:
Отсюда находим значение постоянной баллистического гальванометра:
Зная С, можно использовать баллистический гальванометр для определения напряженности магнитного поля Земли.
ОПРЕДЕЛЕНИЕ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ Для этого необходимо найти отдельно горизонтальную и вертикальную составляющие напряженности геомагнитного поля, а затем с помощью формулы (3) вычислить величину его полной напряженности. Чтобы выполнить эту операцию, достаточно к клеммам индуктора присоединить баллистический гальванометр. Для вычисления горизонтальной составляющей напряженности магнитного поля Земли нужно совместить плоскости обеих колец (А и В) индуктора и установить их по компасу так, чтобы они были перпендикулярны плоскости магнитного меридиана. Затем следует быстро повернуть за головку С оба кольца на 180о, отметив при этом угол β отброса «зайчика» (шкалы) гальванометра. Тогда Q=Cβ, (23) где С – постоянная баллистического гальванометра (22); β – угол отброса «зайчика» (шкалы) гальванометра. С другой стороны, при вращении индуктора в магнитном поле, количество электричества выражается формулой (сравните с формулой 18):
где Ф1 – поток магнитной индукции через площадь кольца В до поворота индуктора на 180о; Ф2 – поток магнитной индукции через ту же площадь после поворота индуктора на 180о; N3 – число витков провода на кольце В индуктора; R3 – сопротивление всех проводников, составляющих замкнутую цепь. Поворот рамки на 180о равносилен замене знака у Ф1 на противоположный, то есть Ф2= Ф1 =Ф. Следовательно, Ф2 Ф1 = 2Ф. (25) Не трудно заметить, что Ф = μоμНГS3, (26) где S3 – площадь кольца В индуктора. Подставляя (26) с учетом (25) в формулу (24), получим:
Из (27) выражаем искомую НГ:
Если в цепь с гальванометром одновременно включить последовательно соединенные индуктор и вторичную катушку, то сопротивление этой цепи, очевидно, будет одно и то же и при измерении постоянной баллистического гальванометра и при измерении НГ, то есть R2 = R3 = R. (29) В этом случае, подставляя в формулу (28) выражение постоянной баллистичес-кого гальванометра (22) и производя соответствующие сокращения, получим окончательно:
Для вычисления вертикальной составляющей напряженности магнитного поля Земли НВ также необходимо совместить плоскость обоих колец (А и В) индуктора и установить их параллельно плоскости магнитного меридиана. Последнее позволяет повысить точность измерения. Затем повернуть за головку Е кольцо В на 90о около горизонтальной оси, отметив при этом отброс «зайчика» (шкалы) гальванометра γ. Тогда количество электричества Q, прошедшего через индуктор и гальванометр, по аналогии с (23) будет равно: Q = Сγ. Дальнейшие рассуждения также аналогичны выше приведенным в отношении определения НГ. Отличие заключается в том, что поворот кольца В проходит не на 180о, а на 90о. Причем первоначальное его положение соответствует Ф1 =0, а так как а не 2 Ф, как в случае с НГ. Следовательно, в окончательных формулах:
или
двоек в знаменателях уже не будет.
Экспериментальная часть ОПИСАНИЕ УСТАНОВКИ Собрать электрическую цепь по схеме (рис. 3)
Рис.3 где Z – индуктор; G – баллистический гальванометр; А – амперметр; Е – источник постоянного напряжения; L1, L2 – нормальный и баллистический соленоиды; К1, К2 – ключи цепей с нормальным и баллистическим соленоидами; R – реостат. ПАРАМЕТРЫ ИНДУКТОРА И СОЛЕНОИДОВ. Число витков индуктора N3 = 150 Диаметр индуктора d3 = 28 см. Число витков нормального соленоида N1 = 600, Длина нормального соленоида ℓ1 = 86,5см, Диаметр сечения нормального соленоидаd1 = 3,1 см, Число витков баллистического соленоида N2 =1500,
ВЫПОЛНЕНИЕ РАБОТЫ
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.159.163 (0.008 с.) |

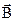 . На рисунке 1 изображены силовые линии магнитного поля Земли, где N и Ѕ – обозначают северный и южный полюсы. Плоскость, которая проходит через магнитные полюсы, называется плоскостью магнитного меридиана. Через каждую точку экватора можно провести свою плоскость магнитного меридиана. Магнитные силовые линии лежат в плоскостях магнитных меридианов, причем на экваторе они располагаются горизонтально.
. На рисунке 1 изображены силовые линии магнитного поля Земли, где N и Ѕ – обозначают северный и южный полюсы. Плоскость, которая проходит через магнитные полюсы, называется плоскостью магнитного меридиана. Через каждую точку экватора можно провести свою плоскость магнитного меридиана. Магнитные силовые линии лежат в плоскостях магнитных меридианов, причем на экваторе они располагаются горизонтально.
 . (1)
. (1) и
и  . Вектор
. Вектор  в этом случае будет перпендикулярен к обоим указанным векторам.
в этом случае будет перпендикулярен к обоим указанным векторам. :
: , (2)
, (2)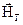 , направленную горизонтально, и
, направленную горизонтально, и 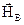 , направленную вертикально. Первая составляющая называется горизонтальной, а вторая - вертикальной составляющей напряженности магнитного поля земного магнетизма. Поскольку
, направленную вертикально. Первая составляющая называется горизонтальной, а вторая - вертикальной составляющей напряженности магнитного поля земного магнетизма. Поскольку 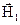 ,
, 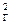 + Н
+ Н  . (3)
. (3)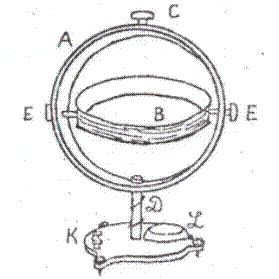
 , (8)
, (8)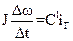 (9)
(9)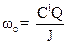 . (11)
. (11)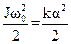 (12)
(12)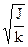 .
.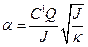 =
= 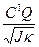 . (13)
. (13)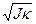 /С1 называется постоянной баллистического гальванометра. Таким образом, угол поворота рамки баллистического гальванометра прямо пропорционален количеству электричества, прошедшего через эту рамку.
/С1 называется постоянной баллистического гальванометра. Таким образом, угол поворота рамки баллистического гальванометра прямо пропорционален количеству электричества, прошедшего через эту рамку.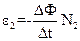 , (15)
, (15) и нормалью к площади Ѕ.
и нормалью к площади Ѕ. , (17)
, (17)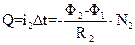 (18)
(18)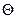 = 0 (соs
= 0 (соs 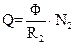 (19)
(19)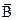 (2), а следовательно
(2), а следовательно 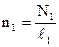 - плотность намотки провода в этом соленоиде.
- плотность намотки провода в этом соленоиде.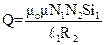 (21)
(21)
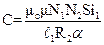 (22)
(22)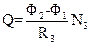 , (24)
, (24)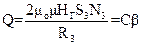 . (27)
. (27) . (28)
. (28)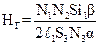 . (30)
. (30) перпендикулярно нормали к площади этого кольца и соs 90о = 0. Поэтому Ф2 – Ф1 = Ф2 = Ф,
перпендикулярно нормали к площади этого кольца и соs 90о = 0. Поэтому Ф2 – Ф1 = Ф2 = Ф,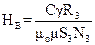 ,
, (31)
(31)



