
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Снятие кривой намагничивания и наблюдение петли гистерезисаСодержание книги
Поиск на нашем сайте
1.Цель работы: Изучить магнитные свойства веществ и методику определения кривой намагничивания и петли гистерезиса.
Теоретическая часть При помещении любого тела в магнитное поле с индукцией
Причины создания собственного магнитного поля
где Sк площадь, ограниченная этим контуром (орбитой k -го электрона);
Рис. 1 Магнитный момент
Для характеристики степени намагниченности вещества введено понятие удельной намагниченности или просто намагниченности
Наличие намагниченности
где µо = 12,5·10-7Гн/м коэффициент пропорциональности, называемый магнитной постоянной. С учетом формулы (5) формулу (1) для результирующего поля в веществе можно переписать в таком виде:
МОЛЕКУЛЫ В МАГНИТНОМ ПОЛЕ
При помещении вещества в магнитное поле 1. Возникает наведенный орбитальный магнитный момент молекулы Как известно, при помещении замкнутого контура с током в магнитное поле М = РmВ sin α, (7) где угол α угол между То же самое происходит и с замкнутым орбитальным током. Однако в связи с тем, что последний распределен по орбите неравномерно, вместо поворота возникает так называемое процессионное движение орбиты электроны. Следовательно, возникает и связанное с орбитой процессионное движение орбитального магнитного момента
Рис. 2 Такое движение вектора
При помещении вещества во внешнее поле 2. Если элементарный магнитный момент Мj = РmjВ sin α. (9) В этом случае процессионное движение не появляется, так как в молекулу входит много движущихся электронов. Следовательно, результирующий орбитальный ток молекулы распределен по некоторой усредненной орбите более равномерно, чем в предыдущем случае. Аналогия его с постоянным током в замкнутом контуре будет более полной. Под действием приложенного вращательного момента
3. Ориентации всех молекулярных В результате воздействия на молекулы помещенного во внешнее магнитное поле Введем новую характеристику результирующего поля в веществе – напряженность магнитного поля
Опыт показывает, что вектор
где х – характерная для данного вещества величина, называемая магнитной восприимчивостью. Согласно (10) размерность Подставив в (10) выражение (11) для
Выразив из (12) вектор
Безразмерная величина µ = 1+х (14) называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества. С учетом (14) формула (13) преобразуется к виду:
С целью выяснения физического смысла µ подставим в (10) выражение индукции
Следовательно, индукция
Таким образом, относительная магнитная проницаемость показывает, во сколько раз усиливается поле в магнетике.
ДИАМАГНЕТИКИ, ПАРАМАГНЕТИКИ И ФЕРРАМАГНЕТИКИ Все вещества при рассмотрении их магнитных свойств принято называть магнетиками. По своим магнитным свойствам магнетики подразделяются на три основные группы: диамагнетики, парамагнетики и феррамагнетики. Диамагнетиками называются вещества, которые намагничиваются во внешнем поле в направлении, противоположном направлению вектора магнитной индукции поля. Их элементарные Диамагнетиками являются инертные газы, водород, азот, висмут, цинк, медь, золото, серебро, кремний, германий, вода, ацетон, глицерин, нафталин и многие другие неорганические и органические соединения. При внесении диамагнетика во внешнее магнитное поле он приобретает, в связи с появлением процессионных движений, наведенный магнитный момент Парамагнетиками называются вещества, которые намагничиваются во внешнем магнитном поле вектора
Намагниченность Ферромагнетиками называются вещества, которые при отсутствии внешнего магнитного поля могут характеризоваться отличной от нуля намагниченностью. Последняя сильно изменяется под влиянием внешних воздействий – магнитного поля, деформации, температуры. Внутреннее магнитное поле ферраманетиков может в тысячи раз превосходить внешнее поле, то есть µ>> 1. Такими свойствами обладает железо, кобальт, никель, чугун, их сплавы. Магнитная проницаемость, например, железа может быть более 10000, а его сплава с никелем (пермаллой -68) - 250000. В настоящей лабораторной работе нас будут интересовать вещества, принадлежащие к третьей группе – феррамагнетики, в частности, железо. Рассмотрим графически зависимость намагничивания железа от напряженности намагничивающего поля
Рис.3
Мы видим, что намагниченность Зависимость магнитной индукции
Рис.4 Зависимость магнитной проницаемости µ от напряженности внешнего поля
Рис.5 Указанные особенности поведения феррамагнетиков связаны с тем, что весь объем феррамагнитного образца как бы разделен на небольшие области – домены, которые самопроизвольно намагничены до насыщения. Линейные размеры доменов порядка 10-3 – 10-2 см. В размагниченном образце в отсутствие внешнего магнитного поля магнитные моменты доменов ориентированы так, что результирующая намагниченность образца в целом равна нулю. При включении поля намагничивание происходит за счет двух процессов: изменения размеров доменов в результате смещения их границ и вращения магнитных моментов доменов. В процессе изменения размеров доменов те из них, которые самопроизвольно намагничены в направлениях, близких к индукции внешнего поля, увеличиваются за счет уменьшения размеров остальных доменов. При намагниченности, близкой у насыщению, начинает проявляться эффект вращения магнитных моментов доменов.
МАГНИТНЫЙ ГИСТЕРЕЗИС Явление магнитного гистерезиса заключается в том, что намагничивание На рисунке 6 приведен график процесса намагничивания и размагничивания железа.
рис.6 Точка О характеризует исходное положение: напряженность внешнего намагничивающего поля равна нулю, и в соответствии с этим намагниченность железа тоже равна нулю. По мере увеличения напряженности Отрезок ОС показывает, что при напряженности внешнего поля, равного нулю, имеется остаточная намагниченность железа. Для того, чтобы совершенно размагнитить железо необходимо приложить к железу намагничивающее поле
ПОЛУЧЕНИЕ КРИВЫХ НАМАГНИЧИВАНИЯ Целью экспериментальной части работы является снятие кривых намаг-
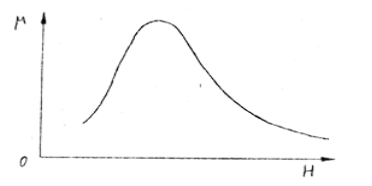
ничивания: В = f1(Н) и µ = f2(Н) Приведенные формулы показывают, что для построения требуемых кривых необходимо знать величину магнитной напряженности Известно, что напряженность магнитного поля внутри замкнутого соленоида определяется по формуле:
где i – сила тока; N1- число витков первичной катушки соленоида;
Так как в данной работе будем пользоваться переменным током, то беря эффективное значение силы тока
Для определения магнитной индукции i = iо sin ω t, где iо – амплитудное значение силы тока; ω – циклическая частота, равная 2πυ, где υ = 50 с-1; t- время Магнитный поток в соленоиде, вызываемый электрическим током, в соответствии с формулой (15) и (18) изменяется по аналогичному закону: Ф = Ф0sin ωt (20) где Фо – максимальное значение магнитного потока. Вследствие того, что вторичная обмотка трансформатора будет находиться в переменном магнитном поле первичной обмотки, во вторичной обмотке будет индуцироваться электродвижущая сила Е, равная
где N2 – число витков вторичной обмотки трансформатора. Подставляя в формулу (21) выражение (20) и производя дифференцирование, получим: E = ωN2Ф0соs ωt. (22) Так как Φ0 = B0 S, (23) где S площадь поперечного сечения трансформатора, то подставляя это выражение в формулу (22), будем иметь E = ωN2B0 S соs ωt. (24) Максимальное амплитудное значение электродвижущей силы Ео получится при условии соs ωt = 1; тогда E0 = ωN2B0 S. (25) Так как вольтметр показывает не амплитудное, а эффективное значение, то
отсюда
Таким образом, измеряя силу тока iэф первичной обмотки трансформатора и значение ЭДС во вторичной обмотке (Еэф), можно по формулам (19 и 27) определить значения Но и Во для различной силы тока и ЭДС. Экспериментальная часть ОПИСАНИЕ УСТАНОВКИ Для выполнения работы необходимо собрать электрическую цепь по следующей схеме (рис. 7):
Рис. 7 ТР1 – вспомогательный понижающий разделительный трансформатор ЭО электронный осциллограф Т Р2 основной трансформатор V вольтметр переменного тока 0-50В А амперметр переменного тока 0 – 1А R1 и R2 реостаты Параметры трансформатора ТР2
N1 = 600 витков N2 =1200витков S = 6,25см2
ВЫПОЛНЕНИЕ РАБОТЫ СНЯТИЕ КРИВЫХ НАМАГНИЧИВАНИЯ 1. При помощи R1 изменяют силу iэф в первичной цепи трансформатора от 0 до 0.5А. Это изменение будет вызывать изменение напряжения Еэф во второй цепи трансформатора. Показание вольтметра снимать через каждые 50мА в первичной цепи. Результаты измерений занести в таблицу. 2. Пользуясь формулами (19) и (27), вычислить для каждого наблюдения напряженность Но и индукцию Во магнитного поля. С помощью формулы (15) на основании вычисленных значений Но и Во определить относительную магнитную проницаемость µ /µо = 12,6·10-7Гн/м. Полученные результаты занести в таблицу. 3. На основании данных, полученных при выполнении предыдущего пункта 2, построить два графика зависимостей Во = f! (Н0) и µ= f2 (Н0).
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.239.189 (0.011 с.) |

 оно начинает создавать собственное или внутреннее магнитное поле с индукцией
оно начинает создавать собственное или внутреннее магнитное поле с индукцией  . Оба поля, накладываясь друг на друга образуют некоторые результирующее магнитное поле в веществе
. Оба поля, накладываясь друг на друга образуют некоторые результирующее магнитное поле в веществе 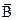 :
: . (1)
. (1) :
: , (2)
, (2) единичная нормаль к площадке Sк, выбираемой по правилу правого винта (рис. 1).
единичная нормаль к площадке Sк, выбираемой по правилу правого винта (рис. 1).
 :
: (3)
(3)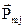 называют также элементарным магнитным моментом. Если элементарные магнитные моменты равны нулю или расположены в теле хаотично, то результирующий магнитный момент тела также равен нулю. Тело в этом случае оказывается ненамагниченным. В противном случае существует не равный нулю результирующий магнитный момент тела.
называют также элементарным магнитным моментом. Если элементарные магнитные моменты равны нулю или расположены в теле хаотично, то результирующий магнитный момент тела также равен нулю. Тело в этом случае оказывается ненамагниченным. В противном случае существует не равный нулю результирующий магнитный момент тела. , которая определяется отношением суммы магнитных моментов всех
, которая определяется отношением суммы магнитных моментов всех  молекул, входящих в тело, к объему этого тела V:
молекул, входящих в тело, к объему этого тела V: (4)
(4) . Связь между
. Связь между  , (5)
, (5) (6)
(6) его молекулы могут испытать три вида различных воздействий и связанных с ними изменений.
его молекулы могут испытать три вида различных воздействий и связанных с ними изменений. , направленный в противоположную сторону по отношению к
, направленный в противоположную сторону по отношению к  возникает вращательный момент
возникает вращательный момент  , который стремится повернуть контур таким образом, чтобы его магнитный момент
, который стремится повернуть контур таким образом, чтобы его магнитный момент  совпадал по направлению с
совпадал по направлению с 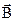 :
: . Оно заключается в том, что конец вектора
. Оно заключается в том, что конец вектора 
 , ослабляющий внешнее магнитное поле. Причем, чем сильнее внешнее поле, тем больше величина
, ослабляющий внешнее магнитное поле. Причем, чем сильнее внешнее поле, тем больше величина 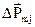 будет равен, очевидно, векторной сумме наведенных орбитальных моментов электронов, входящих в данную молекулу:
будет равен, очевидно, векторной сумме наведенных орбитальных моментов электронов, входящих в данную молекулу: . (8)
. (8) , приложенный ко всей j - ой молекуле:
, приложенный ко всей j - ой молекуле: магнитный момент молекулы
магнитный момент молекулы 
 зависят от температуры. Чем больше температура, тем меньше
зависят от температуры. Чем больше температура, тем меньше  . Очевидно, этот эффект возникает только при условии, что
. Очевидно, этот эффект возникает только при условии, что 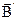 вещества трех указанных факторов в этом веществе и возникает внутреннее магнитное поле
вещества трех указанных факторов в этом веществе и возникает внутреннее магнитное поле  (5). В итоге образуется результирующее поле
(5). В итоге образуется результирующее поле  :
: . (10)
. (10) , (11)
, (11) . (12)
. (12) . (13)
. (13) . (15)
. (15) (16)
(16) (17)
(17)


 ); тогда, при некотором значении Нк, выражаемой отрезком ОД, намагниченность
); тогда, при некотором значении Нк, выражаемой отрезком ОД, намагниченность 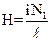 , (18)
, (18) - длина средней линии соленоида, (измеряется по периметру средней линии сердечника).
- длина средней линии соленоида, (измеряется по периметру средней линии сердечника). получим
получим , (19)
, (19) , (21)
, (21) , (26)
, (26) (27)
(27)
 = 10 см.
= 10 см.


