
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отсюда сила, действующая на электрон, будет равнаСодержание книги
Поиск на нашем сайте
F = Ee (9) Ввиду того, что напряженность поля постоянного тока имеет постоянное значение, т.е. на электроны действует постоянная сила, то движение электронов будет равномерно ускоренным. Скорость этого движения в конце интервала времени t определяется уравнением: V = at (10) где а – ускорение t – время пробега электрона между двумя столкновениями электрона с узлами кристаллической решетки. Сила, действующая на электрон со стороны электрического поля, кроме выражения (9), может быть написана по закону Ньютона: F =ma (11) Объединяя формулы (9) и (11), получим eE = ma (12) Отсюда A = Время пробега электрона между двумя столкновениями определяется выражением: t = где
Подставив значение ускорения (13) и время (14) в формулу (10), получим конечную скорость направленного движения электрона к моменту столкновения электрона с узлом кристаллической решетки:
Для закона Ома необходимо знать не конечную скорость движения электрона, а скорость среднюю (Vср)
Ввиду того, что Vо после соударения с узлом кристаллической решетки равна нулю, средняя скорость будет выражаться формулой:
Подставляя значение средней скорости в формулу (8), получим следующее выражение для плотности тока:
Так как выражение
Следовательно, формула плотности тока принимает вид: i = σE (20) Полученное выражение для плотности тока полностью совпадает с формулой (7). Целью настоящей работы является проверка закона Ома для различных случаев соединения проводников. Сопротивления можно включить в электрическую цепь последовательно и параллельно. Пусть три сопротивления соединены последовательно (рис.1)
Рис.1 Так как при последовательном соединении проводников сила тока в них одина-кова, то:
или Jr1 = UA-UB; Jr2 = UB-BC; Jr3= UC-UД Складывая эти уравнения почленно, получим:
Пусть общее сопротивление участка цепи от А до Д равняется к; тогда
Сравнивая уравнения (22) и (23), получим: r1+r2+r3 = r (24) Общее сопротивление проводников при последовательном соединении равно сумме сопротивлений отдельных проводников, составляющих соединение. Пусть далее три проводника соединены параллельно (рис.2)
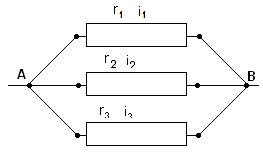
Рис.2 Обозначим потенциал в точке А черезUA и в точке В через UB. Силу тока в отдельных проводниках соответственно обозначим: i1, i2, i3 Для каждой ветки параллельного соединения можно написать:
Сложив почленно последние равенства (25), находим:
где J =i1 + i2 + i3
Обозначим через R сопротивление такого проводника, который, будучи введен вместо трех данных между А и В, заменит их так, что сила тока в цепи останется прежней J, тогда:
Подставив это значение в формулу (25’), получим:
Сокращая на
где: При параллельном соединении проводников проводимость всего разветвления равна сумме проводимостей отдельных проводников, входящих в разветвленную цепь. Теория мостика Уитстона основана на законах Кирхгофа. Первый закон Кирхгофа говорит: алгебраическая сумма всех токов в каждой точке разветвления равна нулю. Это означает, что какое количество электричества притекает к точке разветвления, такое же количество электричества и уходит из этой точки разветвления.
Рис.3 При этом токи, приходящие к узлу Р (рис.3), следует брать со знаком плюс, а токи отходящие от узла Р – со знаком минус. Для случая, изображенного на рис.3, имеем: J1 – J2 + J3 – J4 = 0 (27) Второй закон Кирхгофа является обобщением закона Ома для разветвленной цепи. Согласно этому закону, во всяком замкнутом контуре, произвольно. Выведенном в разветвленной сети проводников, алгебраическая сумма произведений силы тока на соответствующее сопротивление равна алгебраической сумме ЭДС, содержащихся в этом замкнутом контуре.
Для составления уравнений по второму закону Кирхгофа выбирают какое-нибудь направление обхода контура (например, по часовой стрелке), тогда токи, направление которых совпадает с выбранным направлением, считаются положительными, а токи противоположного направления – отрицательными. Вводится условие и для определения знака электродвижущей силы. Если при обходе контура приходится проходить через источник тока от отрицательного полюса к положительному, то ЭДС такого источника принято считать положительной. Если в выбранном контуре ЭДС отсутствует, то
Применим законы Кирхгофа к мостику Уитстона. Схема мостика дана на рис.4
Рис.4 Четыре сопротивления rx, r2, r3, r4 образуют плечи мостика. В одну диагональ моста (АВ) включена батарея с ЭДС, равной Е, и внутренним сопротивлением, равным R. В другую диагональ (ДС) включен гальванометр (q) с сопротивлением r. Уравнение первого закона Кирхгофа для узлов А, Д и В имеют вид: Для узла А: J –i1 –i3 = 0 Для узла Д: i1- i2 - i = 0 Для узла В:i2 + i4 –J =0 (30) Для узла С: i3 + i-i4 = 0 Легко видеть, что уравнение для узла С ничего нового не дает, так как является следствием из решения предыдущих 3 уравнений (30). Уравнения второго закона Кирхгофа для замкнутых контуров будут: контур АДСА: i1rx+ir-i3r3 = 0 ДВСД i2r2 - i4r4-ir = 0 (31) Если ток, идущий через гальванометр равен нулю (i=0), то уравнения (30), содержащие i, примут вид: i1= i2 i3 = i4 (32) а из уравнений (31) получим: i1rx=i3r3 i2r2 = i4r4 (33) Разделим почленно уравнения (33)
Принимая во внимание уравнения (32), получим
Если сопротивления r3 и r4 сделаны из однородного провода, то есть одинакового сечения и из одинакового материала, то отношение сопротивлений r3 и r4 можно заменить отношением их длин:
где ℓ1 -длина участка провода АС; ℓ2 - длина участка провода СВ Тогда
ОПИСАНИЕ ПРИБОРА Мостик Уитстона состоит из известного сопротивления(штепсельного магазина сопротивления) R, реохорда АВ, гальванометра q, неизвестного сопротивления, которое требуется определить в настоящей работе. Ток к мостику подводится от аккумулятора Е через ключ К1 и реостат R1. Реохордом называется линейка с делением, на которую натянута однородная проволока с большим удельным сопротивлением и постоянным по всей ее длине сечением. Вдоль проводника может перемещаться подвижной контакт С.
ВЫПОЛНЕНИЕ РАБОТЫ 1. Собрать мостик Уитстона по схеме (рис.5)
Рис.5 2. В магазине сопротивления R ввести сопротивление 200 – 400 Ом. 3. Подвижной контакт реохорда С установить приблизительно на середине реохорда. 4. Включить ток коротким замыканием ключа К1, заметить направление отклонения стрелки гальванометра и путем передвижения подвижного контакта найти на реохорде АВ такую точку C, для которой при коротких включениях тока стрелка гальванометра не отклонялась бы 5. Измерить длины АС и СВ по линейке реохорда и вычислить сопротивление rх, по формуле (36). 6. Заменить катушку сопротивления rх, сопротивлением rх2; проделать действия, указанные в п.4 и 5 и определить величину сопротивлений этих катушек. 7. Соединить 2 катушки сопротивления последовательно (рис.1) пользуясь мостиком Уитстона, определить сопротивление 2 катушек, соединенных последовательно. 8. Соединить катушки сопротивления параллельно (рис.2) и, пользуясь мостиком Уитстона (как и в пункте 7), определить экспериментально сопротивление 2 катушек при их параллельном соединении. 9. Произвести теоретический подсчет последовательно и параллельно соединенных сопротивлений по формулам (24) и (26) 10. Полученные данные занести в таблицу.
КОНТРОЛЬНЫЕ ВОПРОСЫ. 1. Ц ель и производство работы 2. Постоянный электрический ток, его характеристики и условия существования. Электродвижущая сила источника тока. 3. Закон Ома для участка цепи в интегральной и дифференциальной формах. Закон Ома для замкнутой цепи. 4. Классическая электронная теория электропроводимости металлов и её опытные обоснования. Вывод закона Ома в дифференциальной форме из электронных представлений. 5. Сопротивление проводников. Способы соединения проводников. Вывод формул для расчета сопротивлений из последовательно и параллельно включенных резисторов. 6. Работа и мощность тока. Коэффициент полезного действия источника тока. 7. Схема моста Уитстона. Применение правил Кирхгофа для расчета неизвестного сопротивления методом моста Уитстона. Работа № 10
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

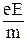 (13)
(13) , (14)
, (14) – средняя длина пути свободного пробега электрона;
– средняя длина пути свободного пробега электрона; – средняя скорость беспорядочного теплового движения электронов.
– средняя скорость беспорядочного теплового движения электронов. (15)
(15) (16)
(16)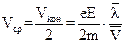 (17)
(17) (18)
(18) состоит из постоянных для данной температуры величин, характеризующих состояние данного проводника с точки зрения его способности проводить эклектический ток, все это выражение имеет физический смысл проводимости проводника (σ)
состоит из постоянных для данной температуры величин, характеризующих состояние данного проводника с точки зрения его способности проводить эклектический ток, все это выражение имеет физический смысл проводимости проводника (σ) (19)
(19)
 (21)
(21) (22)
(22) (23)
(23)
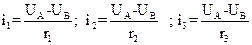 (25)
(25) (25’)
(25’)

 , будем иметь
, будем иметь , (26)
, (26) - называется проводимостью проводника.
- называется проводимостью проводника.
 (28)
(28) (29)
(29)

 (34)
(34)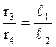 , (35)
, (35) (36)
(36)
 АС
(СМ)
АС
(СМ)
 (Ом)
(Ом)



