
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение электрического поляСодержание книги
Поиск на нашем сайте 1. Цель работы: Изучение электрических полей, т.е. требуется найти эквипотенциальные поверхности и изобразить электрическое поле при помощи вектора напряженности.
Теоретическая часть Электрическое поле- это особый вид материи, посредством которой взаимодействуют электрические заряды. Всякий заряд, помещенный в это поле, подвергается действию силы. Для точечных зарядов: F = K где К – коэффициент пропорциональности в системе СИ
где εо – электрическая постоянная; εо = 8,85 ·10-12ф/м; r - расстояние между зарядами; Q – заряд, образующий поле; Qо - пробный заряд. Электрическое поле имеет две характеристики: 1) силовую; 2) энергетическую Мерой силового проявления электрического поля является напряженность- Величина напряженности электрического поля, создаваемого точечным зарядом Q, определяется по формуле: E= где Q – заряд, образующий электрическое поле; r - расстояние от заряда до точки, где определяется напряженность электрического поля. Электрическое поле можно изобразить графически при помощи линий вектора напряженности(силовых линий). Линией вектора напряженности электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля. Силовые линии точечного заряда представляет собой совокупности радиальных прямых, направленных от заряда, если он положителен и к заряду, если он отрицателен (рис.1).
Рис.1
Напряженность электрического поля Е можно определить числом силовых линий N, пронизывающих единичную площадку S, помещенную в данную точку электрического поля перпендикулярно к направлению силовых линий. E= Величина N=ЕS называется потоком напряженности. Различают два вида электрических полей: поле неоднородное, для которого напряженность в различных точках различна, например, поле точечного заряда. Поле однородное, для которого напряженность в различных точках одинакова, например, поле плоского конденсатора. Мерой энергетического проявления электрического поля является потенциал. На всякий заряд Qо, находящийся в электрическом поле, действует сила, которая может перемещать этот заряд. Работа перемещения заряда в электрическом поле выражается формулой:
Величина -
Знак минус показывает, что при перемещении заряда силами поля его потенциальная энергия убывает, переходя в работу перемещения. Работа перемещения заряда не зависит от формы пути, а зависит только от равенства потенциалов начальной и конечной точек пути. A = Qo (φ1 – φ2) где φ1 и φ2 потенциалы в поле точечного заряда соответственно на расстоянии r1 и r2 от заряда Q
Потенциал данной точки поля определяется работой, которую совершают силы поля при перемещении единичного положительного заряда из данной точки поля в бесконечно удаленную, потенциал которой равен нулю.
Единица потенциала в системе СИ [φ] = Потенциал электрического поля представляет собой функцию, меняющуюся от точки к точке, но можно выделить совокупность точек, потенциалы которых равны. Геометрическое место точек постоянного потенциала называют эквипотенциальной поверхностью(рис. 2) Пусть АВ эквипотенциальная поверхность. Рассмотрим работу перемещения заряда на отрезке Δх вдоль линии АВ. ΔА =FΔх соs α = ЕQоΔх·соs α, где α- угол между направлением силы F и перемещением Δх.
Рис.2 Из формулы А = Qо (φ1 – φ2) следует, что работа перемещения заряда вдоль эквипотенциальной поверхности равна нулю: φ1 = φ2. Следовательно, QЕ Δх соs α = 0, но величины Q, Е, Δх не равны нулю, нулю должен равняться косинус α, такое может быть при α=90о, а это означает, что вектор напряженности электрического поля перепендикулярен эквипотенциальной поверхности. Напряженность и потенциал имеют связь между собой.
Напряженность равна градиенту потенциала, а минус показывает на то, что напряженность поля направлена в сторону убывания потенциала. Если в однородное электрическое поле поместить проводник, то под влиянием поля свободные электроны проводника начнут перемещаться против воли. Если в электрическое поле поместить металлический шар, то левая часть шара зарядится отрицательно, а правая положительно. Это явление носит название электростатической индукции. Перемещение зарядов в проводнике будет происходить до тех пор, пока внешнее поле внутри проводника не скомпенсируется собственным полем зарядов. Поле внутри проводника станет равным нулю (рис. 3). Это означает, что все-таки точки проводника имеют одинаковый потенциал, т.е. поверхность проводника является эквипотенциальной поверхностью. Следовательно, силовые линии поля вблизи проводника перпендикулярны эквипотенциальным поверхностям.
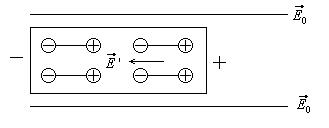
Рис.3 Электрическое поле будет отсутствовать но только внутри сплошного проводника, но и внутри полостей, имеющихся в проводнике, например внутри металлического кольца. Это свойство проводников используется в качестве электростатической защиты. Если поместить в электрическое поле диэлектрик, то под влиянием электрического поля все дипольные молекулы(подобные электрическому диполю)диэлектрика повернутся так, что их оси распложаться вдоль силовых линий поля. Таким образом, под действием внешнего электрического поля диэлектрик поляризуется, что ведет к ослаблению поля внутри диэлектрика. Так, если поместить в однородное электрическое поле диэлектрик, поляризуясь, он, создает свое собственное поле Е’ направленное против внешнего поля
Рис.4
ВЫПОЛНЕНИЕ РАБОТЫ Принадлежности и приборы: ванна с дистиллированной водой, набор металлических электродов,(Плоский, точечный) катодный вольтметр, источник тока, проводники.
1. Собрать электрическую цепь согласно схемы.(рис.5) 2. В ванну с дистиллированной водой устанавливают исследуемые электроны: а) два точечных или б) два плоских. 3. Включают катодный вольтметр в сеть при помощи вилки. Загорается индикаторная лампочка. Через 1-2 минуты (по мере нагревания лампы) стрелка вольтметра отклоняется вправо, а затем устанавливается на нуле. После этого вольтметром можно пользоваться. Для чего: а) посмотреть постоянный или переменный ток подается на электроды и поставить вольтметр на соответствующую отметку ( б) посмотреть величину напряжения, подаваемого на электроды и поставить вольтметр в соответствующее положение; в) выбрать шкалу, которой лучше пользоваться и определить цену деления данной шкалы. 4. Подать напряжение на электроды. 5. Металлический зонд С приводят в соприкосновение с электродом В и устанавливают стрелку вольтметра на нуль шкалы. 6. Измеряют координаты точек с равным потенциалом (не менее шести точек) для ЗВ, 8В,9В,12В в случаях: а) два точечных; б) плоский и точечный. Данные записываются в таблицу. 7. Поставить два плоских электрода, а между ними металлическое кольцо и измерить координаты точек одинакового потенциала вне кольца и внутри кольца. Данные записать в таблицу. 8. Пункт 7 повторить, заменив металлическое кольцо кольцом из органического стекла.
9. Построить графики электрических полей, образованных: 1) двумя точечными электродами, 2) двумя плоскими электродами.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Цель и производство работы. 2. Электрический заряд. Принцип квантования заряда. Закон сохранения заряда. Закон Кулона. 3. Электрическое поле. Основные характеристики электрического поля – напряженность и потенциал поля. Напряженность как градиент потенциала. 4. Напряженность поля точечного заряда. Расчё1т электростатических полей методом суперпозиции. 5. Поток вектора напряженности. Теорема Остроградского – Гаусса и её применение к расчёту электрических полей бесконечной прямолинейной равномерно заряженной нити, бесконечной равномерно заряженности плоскости, плоского конденсатора. 6. Электрическое поле в веществе. Проводники и диэлектрики в электрическом поле. Явления электромагнитной индукции и поляризации диэлектрика. Относительная диэлектрическая проницательность среды.
Работа № 3 ОПРЕДЕЛЕНИЕ ЭЛЕКТРОЁМКОСТИ И ЭНЕРГИИ КОНДЕНСАТОРОВ ПРИ ПОМОЩИ ГАЛЬВАНОМЕТРА 1.Цель работы: Изучить методы определения ёмкости и энергии конденсаторов последовательном и параллельном соединении
Теоретическая часть. Опыт показывает, что при разрядке разных проводников одинаковыми количествами электричества, потенциалы этих проводников оказываются различными. Это говорит о том, что проводники отличаются физическими свойством, которое характеризуется величиной, называемой ёмкостью.
Ёмкостью уединенного проводника (проводника, вблизи которого нет других тел) называется физическая величина, численно равная количеству электричества, которое надо сообщить проводнику, чтобы изменить его потенциал за единицу. За единицу емкости принимает емкость такого проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1 Кл. Эта единица называется фарада (Ф) На практике пользуются единицами, равными долями фарады: микрофарада (1µФ = 10-6Ф), пикофарада (1пФ = 10-12Ф). Уединенные проводники обладают малой емкостью. В практике применяется прибор, емкость которого искусственно увеличена – это конденсатор. В основу устройства конденсаторов положен тот факт, что электроемкость проводника возрастает при приближении к нему других незаряженных тел. Под действием поля, создаваемого заряженным проводником, на поднесенном к нему теле, возникают индуцированные (на проводнике) или связанные (на диэлектрике)заряды. Заряды, противоположные по знаку заряда проводника q располагаются ближе к проводнику, чем одинаковые, с q и следовательно, оказывают большое влияние на его потенциал, т.е. потенциал уменьшается, а электроемкость увеличивается, согласно формулы (1). Конденсаторы делаются в виде двух проводников, расположенных близко друг к другу, разделенных диэлектриком. Конденсаторы бывают разной формы- сферические, цилиндрические и плоские. Емкость плоского конденсатора определяется по формуле:
где q – разряд пластины, Δφ – разность потенциалов между обкладками конденсаторов. Рассмотрим плоский конденсатор, который состоит из двух металлических пластин с площадью S каждая, между которыми находится диэлектрик толщиной d с диэлектрической проницаемостью ε (ε показывает во сколько раз сила взаимодействия двух зарядов в вакууме больше, чем в данный среде). Если конденсатор заряжен, то на его пластинах находится некоторое количество электричества q. Тогда по теореме Остроградского − Гаусса напряженность электрического поля между пластинами
Между потенциалом и напряженностью электрического поля имеется следующая зависимость:
Отсюда определяется разность потенциалов между пластинами конденсатора Δφ
Подставим значение Δφ из формулы (5) в формулу емкости плоского конденсатора. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости (ε), площади пластин (S), и обратно пропорциональна толщине диэлектрика (d). Конденсаторы можно соединить между собой параллельно и последовательно или смешанн. При параллельном соединении конденсаторов все положительно заряженные пластины соединяются между собой и все отрицательные
Поскольку одноименно заряженные пластины соединены вместе, потенциалы всех положительно заряженных пластин будут одинаковыми (также и потенциалы всех отрицательно заряженных пластин), т.е. разность потенциалов на всех конденсаторах будет одинакова, но количество электричества на пластинах различных конденсаторов будет различным. Используя формулу (1) можно записать:
Сложив почленно эти уравнения, получим:
этому выражению можно придать вид
где q = q1+ q2 + q3, т.е. при параллельном соединении конденсаторов общая электроемкость равна сумме электроемкостей всех конденсаторов, взятых в соединении. При последовательном соединении конденсаторы соединяются так, что положительно заряженная пластина первого конденсатора присоединяется к отрицательной пластине второго конденсатора, положительная пластина второго конденсатора присоединяется к отрицательной пластине третьего конденсатора и т.д. Допустим, на одной пластине первого конденсатора при зарядке конденсатора появляется равный заряд – q, а на пластине второго конденсатора равный заряд + q и т.д. Таким образом, на всех пластинах последовательно соединенных конденсаторов будет находится одно и то же количество электричества.
Поскольку вторая пластина первого конденсатора соединена с первой пластиной второго, потенциалы на всех пластинах будут одинаковыми. По этой причине одинаковые потенциалы будут на второй пластине второго конденсатора и первой пластине третьего конденсатора и т.д. Используя формулу (1), можно написать:
Сложим почленно уравнения и получим
Если С С –общая электроемкость всех конденсаторов, соединенных последовательно, тогда по формуле (1) для батареи:
Эта формула (9) соответствует формуле (3) электроемкости, при условии что:
т.е обратная величина электроемкости конденсаторов, соединенных последовательно, равна сумме обратных величин электроемкости всех конденсаторов, составляющих последовательное соединение. Определим энергию заряженного проводника. Нейтральному проводнику, имеющему емкость С, сообщили заряд q (зарядка проводится малыми порциями dq, переносимыми из бесконечности, где потенциал q, на данный проводник). По мере зарядки потенциал проводника возрастает, обозначим этот потенциал dq. Выразим элементарную работу С при переносе заряда dq: dA = (φ0 – φ) = (0 −φ)dq; dA =− dq. Так как dq = Сd φ, то dA =Cφdφ. Полная работа при зарядке проводника равна сумме всех малых работ Аd. А = Эта работа была совершена внешними силами против сил поля заряженного проводника. Поэтому энергия заряженного проводника выражается формулой:
Если выразить С через q и φ, то энергию проводника можно выразить W = Процесс зарядки пластин можно представить как перенос бесконечно малых количеств электричества dq с одной пластины на другую, и для этого надо затратить работу: dА = dq((φ1 – φ2).Следовательно, получили такое же выражение работы, как при заряжении нейтрального проводника, только вместо потенциала φ стоит разность потенциалов Δφ. Полная эе энергия заряженного конденсатора выразиться формулами:
в соответствии с формулой (11), выражающей энергию заряженного проводника. Измерения электроемкости удобно проводить при помощи баллистического гальванометра. Баллистический отличается от обыкновенного гальванометра тем, что при его помощи можно измерить количество электричества q, возникшее за малый промежуток времени (в нашей задаче вследствие кратковременного разряда предварительно заряженного конденсатора). Подвижная система баллистического гальванометра, как и во всяком гальванометре, состоит из подвижной рамки, помещенной между полосами постоянного магнита, с тем только отличием, что конструкция подвижной системы (рамки) подобрана так, что период собственных колебаний рамки получается большим, вследствие этого кратковременный ток, возникающий при разрядке конденсатора через гальванометр, вызывает резкий поворот подвижной системы, а, следовательно, и резкий отброс светового «зайчика» и медленное вращение рамки (и «зайчика») к нулевому положению. Количество электричества кратковременного разряда конденсатора прямо пропорционально углу отброса светового «зайчика». q = κα, где κ − постоянная баллистического гальванометра, Для определения постоянной баллистического гальванометра (κ) можно воспользоваться следующим методом: допустим, что имеется конденсатор, емкость которого (С) известна. Для этого зарядим конденсатор до некоторой разности потенциалов Δφ, тогда исходя из формулы емкости конденсатора: С = Можно написать: q = С Δφ (14) Сравним формулу (13) с формулой (14) имеем: κα = СΔφ (15) Отсюда κ = Таким образом, для вычисления постоянной гальванометра необходимо знать электроемкость какого – нибудь известного конденсатора (с) угол отброса «зайчика» гальванометра (α) и напряжение, поданное для зарядки конденсатора (Δφ).
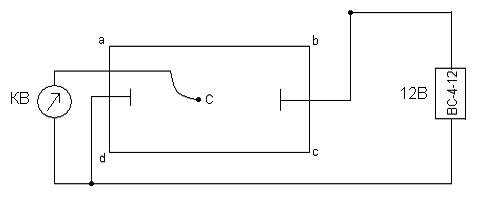
Экспериментальная часть ПРИНАДЛЕЖНОСТИ: баллистический гальванометр, вольтметр, два переключателя с шестью клеммами, набор конденсаторов на специальных панелях, выпрямитель ВСЧ – 12. ЗАДАНИЕ № 1 Определение постоянной баллистического гальванометра. Для этого 1. Собрать электрическую цепь по схеме 1. 2. После проверки электрической цепи а) замерить показания вольтметра Δφ; б) переключателями К включить на зарядку эталонного конденсатора, емкость которого С = 1мкФ 3. Быстро включить переключателем К1 на зарядку конденсатора через 6 баллистический гальванометр и отсчитать в миллиметрах отброс «зайчика» (α). 4. Повторить указанные выше действия не менее пяти раз. Из полученных величин угловых отбросов «зайчика» - вычислить среднюю величину отброса. По формуле (15) вычислить постоянную баллистическую гальванометра (к). 5. Определить электроемкость каждого из двух неизвестных конденсаторов (С1 и С2): а) переключить К1 на зарядку испытуемых конденсаторов; б) определить не менее пяти отбросов «зайчика» для каждого неизвес- тного конденсатора, действуя согласно пунктам 2в и 3; в) вычислить среднюю величину отброса «зайчика» для каждого коден- сатора; г) пользуясь формулой (15), определить величину электроемкости неиз- вестных конденсаторов (С1 и С2). 6. Соединить два неизвестных конденсатора параллельно: а) зная электроемкость каждого конденсатора (см.п.6) теоретически рас- считать электроемкость параллельного соединения конденсаторов пользу ясь соответствующей формулой С = С1 + С2 б) зарядить конденсаторы и пользуясь указаниями п.п.2 и 3 настоящего руководства, определить экспериментально электроемкость последовате- льного соединения конденсаторов, пользуясь теоретическими расчетами. 7. Соединить два конденсатора последовательно и: а) зная емкость каждого конденсатора, вычислить электроемкость после- довательного соединения конденсаторов соответствующей формулой:
б) зарядить конденсаторы и, пользуясь указаниями п.п.2 и 3 настоящего руководства, определить экспериментально электроемкость последовательного соединения конденсаторов и тем дать подтверждения теоретическим расчетам. Зная емкость конденсаторов и напряжение, определить энергию последо- вательного и параллельного соединения по формуле
где С и φ соответствуют определяемому конденсатору или системе конденсаторов Все полученные величины записать в таблицу.
а) определение постоянной баллистической гальванометра
б) определение электроемкости и энергии отдельных конденсаторов
в) определение электроемкости и соединения конденсаторов параллельно:
г) определение электроемкости соединения конденсаторов последовательно:
Схема № 1
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Цель и производство работы. 2. Проводники в электростатическом поле. Поле внутри проводника и у его поверхности. Распределение зарядов в проводнике. 3. Электроемкость уединенного проводника, единицы электроемкости. 4. Взаимная емкость двух проводников, конденсаторов. 5. Вывод формулы плоского конденсатора. 6. Энергия системы зарядов и плоского конденсатора. 7. Соединение конденсаторов.
Работа № 4 ОПРЕДЕЛЕНИЕ ЭЛЕКТРОХИМИЧЕСКОГО ЭКВИВАЛЕНТА МЕДИ 1. Цель работы: Изучить явление электролиза. Определить электрохимческий эквивалент меди.
Теоретическая часть Вещества, растворы которых проводят электрический ток, называются электролитами. К электролитам относятся растворы кислот, щелочей и солей в воде и других растворителях, а также расплавленные соли. Электрический ток в любых электролитах создается движением положительных и отрицательных ионов, т. е. заряженных атомов и молекул вещества. В теории электролитической диссоциации предполагается, что в растворах электролитов часть молекул всегда оказывается диссоциированной. Диссоциация, т. е. распад молекул электролита на ионы, происходит под действием растворителя и совершается непрерывно; одновременно в растворах происходит обратный процесс соединения противоположно заряженных ионов – рекомбинация, в результате которого вновь образуются нейтральные молекулы электролита. В результате в растворах возникает состояние подвижного равновесия, и концентрация ионов в растворе не изменяется так как за единицу времени распадается столько же молекул, сколько образуется новых молекул вследствие воссоединения ионов. Количественной характеристикой состояния диссоциации служит степень диссоциации раствора, которая определяется отношением числа молекул, распавшихся на ионы, к полному числу молекул в растворе. Степень диссоциации зависит от многих условий: от природы электролита, его концентрации в растворе, от температуры и т. д. При повышении температуры электролита возрастает средняя кинетическая энергия теплового движения молекул, увеличивается и число пар ионов, образующихся за единицу времени. Из-за увеличения концентрации ионов при повышении температуры значение электрического сопротивления электролита с повышением температуры уменьшается. Электрическое поле в электролите образуется между электродами, которые соединяются с клеммами источника э. д. с. и погружаются в электролит; электрод, соединенный с положительным полюсом, называется анодом; электрод, соединенный с отрицательным полюсом, называется катодом. Положительные ионы, перемещающиеся в электрическом поле к катоду, называются катионами; отрицательные ионы, перемещающиеся к аноду, называются анионами. При прохождении тока через электролиты (или расплавленные соли) изменяется их химический состав, а на электродах происходит выделение различных веществ. Это явление называется электролизом. Ионы обоих знаков, достигая электродов, или отдают излишние электроны аноду, или принимают недостающие им электроны с катода, тем самым делаются нейтральными молекулами и выделяются на поверхностях электродов, образуя первичные продукты электролиза. Первичные продукты электролиза могут вступать в химические реакции с растворителем и веществом электродов; в результате этого на поверхности выделяются вторичные продукты электролиза, химическая природа которых очень часто оказывается совершенно отличной от природы первичных продуктов. Для электролитов справедлив закон Ома, который записывается в дифференциальной форме следующим образом:
где j – плотность тока, q – заряд иона, n – концентрация ионов, Количественная сторона электрических процессов определяется двумя законами Фарадея. Допустим, что за некоторый промежуток времени на электроде разрядятся N ионов с валентностью z; это означает, что за время t будет перенесен суммарный заряд
где e – заряд электрона. Масса вещества, выделившегося на электроде при электролизе:
где m – масса одного иона (или группы ионов) с зарядом ez. Разделим почленно уравнение (3) на уравнение (2):
или (4)
Правая часть уравнения (4) состоит из постоянных величин, характеризующих те материальные частицы, которые в виде ионов переносят заряды и при разрядке выделяются на электроде; обозначим дробь
Электрохимический эквивалент вещества численно равен тому количеству вещества (в мг), которое выделяется из раствора при прохождении через него одного кулона электричества (для меди его справочное значение k = 0,329 мг/Кл). Выражение (5) можно преобразовать в иную форму:
или (6)
где I – сила тока, t – время. Выражение (6) носит название 1-го закона Фарадея: Количество вещества (в мг), выделяемого током, при прохождении через электролит прямо пропорционально электрохимическому эквиваленту вещества, силе тока (в амперах) и времени (в секундах). Умножим числитель и знаменатель дроби
Произведение m
Отношение атомного веса к валентности называется химическим эквивалентом вещества. Произведение Отсюда получается второй закон Фарадея:
Электрохимический эквивалент данного вещества k прямо пропорционален его химическому эквиваленту Подставляя в уравнение (6) k из выражения (9), получим формулу объединенного закона Фарадея:
Определим физический смысл числа Фарадея:
Опыты Фарадея показали, что для разных электролитов электрохимический эквивалент k вещества оказывается различным, но, чтобы выделить на электроде один моль любого одновалентного вещества, требуется пропустить один и тот же заряд F, равный примерно 96500 Кл·моль-1 (или, более точно 96485 Кл·моль-1). Если 1 моль ионов при пропускании электрического тока через раствор электролита переносит электрический заряд, равный постоянной Фарадея F, то на долю каждого иона приходится электрический заряд, равный
На основании такого расчета ирландский физик Д. Стоней высказал предположение о существовании внутри атомов элементарных электрических зарядов. В 1891 г. минимальный электрический заряд e он предложил назвать электроном. Измерение заряда иона. При пропускании через электролит постоянного электрического тока за время t к одному из электродов приходит электрический заряд, равный произведению силы тока I на время t. С другой стороны, этот электрический заряд равен произведению заряда одного иона q0 на число ионов N:
Отсюда получаем
Так как
то из выражений (14) и (13) находим
Таким образом, для экспериментального определения заряда одного иона нужно измерить силу постоянного тока I, проходящего через электролит, время t пропускания тока и массу m вещества, выделившегося у одного из электродов. Необходимо знать также молярную массу вещества μ.
Для определения электрохимического эквивалента, как видно из формулы (6), необходимо определить величины M, I и t. Для этих измерений обычно применяют особые приборы – вольтаметры. К этому названию часто присоединяют название того элемента, который выделяется на катоде; так, применяются медный вольтаметр, серебряный вольтаметр, водородный вольтаметр и др. Количество вещества, выделяющегося при электролизе, принято определять при помощи взвешивания, силу тока I измеряют при помощи точного амперметра и время t – при помощи секундомера. Применение электролиза. Явление электролиза широко применяется в современном промышленном производстве. С помощью электролиза из солей и оксидов получают металлы. Электролитическим способом получают высокочистые вещества, т. к. при этом образуется малое количество примесей. С целью предотвращения окисления поверхности металлических изделий, а также для повышения его прочности путем эле
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.037 с.) |

 ,
,
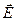 . Напряженность электрического поля в данной точке есть вектор, равный величине силы, действующей на единичный положительный заряд, помещенный в эту точку и совпадающий с ней по направлению.
. Напряженность электрического поля в данной точке есть вектор, равный величине силы, действующей на единичный положительный заряд, помещенный в эту точку и совпадающий с ней по направлению. 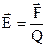
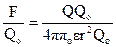 или E =
или E = 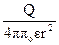


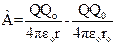
 представляет собой потенциальную энергию Wn заряда Qо в данной точке электрического поля заряда Q:
представляет собой потенциальную энергию Wn заряда Qо в данной точке электрического поля заряда Q: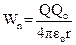
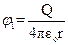 ;
; 





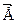 (рис.4). Поэтому результирующая напряженность поля в диэлектрике
(рис.4). Поэтому результирующая напряженность поля в диэлектрике 

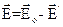
 ,–);
,–); (1)
(1)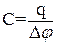 (2)
(2) где
где  ε0 – электрическая постоянная
ε0 – электрическая постоянная 
 (3)
(3) = -
= -  =
= 
 - градиент потенциала. Тогда для конденсатора: где Δφ- разность потенциалов между пластинами конденсаторов, d – расстояние между пластинами, т.е толщина диэлектрика. Из формулы определения
- градиент потенциала. Тогда для конденсатора: где Δφ- разность потенциалов между пластинами конденсаторов, d – расстояние между пластинами, т.е толщина диэлектрика. Из формулы определения  (4)
(4)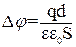 (5)
(5)
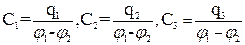 (6)
(6) (7)
(7)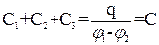

 или
или 
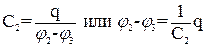 ,
, .
.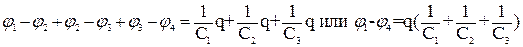 (8)
(8) (9)
(9) (10)
(10) .
. . (11)
. (11) q φ или W
q φ или W  ,
, ,
, (12)
(12) , где q− количество электричества на обкладках конденсатора, Δφ−разность потенциалов на обкладках конденсатора, С − электроемкость конденсатора.
, где q− количество электричества на обкладках конденсатора, Δφ−разность потенциалов на обкладках конденсатора, С − электроемкость конденсатора. .
.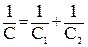 ,
,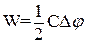 ,
,
 , (1)
, (1) и
и  - подвижности положительных и отрицательных ионов соответственно; E – напряженность электрического поля.
- подвижности положительных и отрицательных ионов соответственно; E – напряженность электрического поля. , (2)
, (2)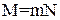 , (3)
, (3)

 через k. Физический смысл этого коэффициента, называемого электрохимическим эквивалентом вещества, ясен из выражения:
через k. Физический смысл этого коэффициента, называемого электрохимическим эквивалентом вещества, ясен из выражения: (5)
(5)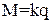
 ,
,
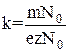 (7)
(7) представляет собой атомный вес (A). Тогда уравнение (7) принимает вид:
представляет собой атомный вес (A). Тогда уравнение (7) принимает вид: (8)
(8) (9)
(9) .
. (10)
(10)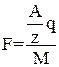 (11)
(11)

 (12)
(12) (13)
(13) , (14)
, (14)



