
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение полной и полезной мощности и коэффициента полезного действия источника постоянного и переменного токаСодержание книги
Поиск на нашем сайте
1. Цель работы: изучение основных законов, наблюдающихся при прохождении постоянного и переменного электрического тока по проводникам.
Теоретическая часть Постоянный ток Упорядоченное движение заряженных частиц называется электрическим током. Сила тока -это скалярная величина, равная заряду, переносимому носителями через площадь поперечного сечения проводника в единицу времени.
(1)
где q- заряд
За направление тока принимается направление, в котором перемещаются положительные заряды. При этом по перемещению заряда в цепи совершают работу сторонние силы. Величина, равная работе сторонних сил, отнесенная к единице положительного заряда, называется электродвижущей силой (э.д.с.) S, действующей в цепи или на её участке. По определению
где А- работа сторонних сил, q- заряд Экспериментально немецкий физик Ом установил, что сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике.
Однородным называется проводник, в котором не действуют сторонние силы. Закон Ома можно записать в дифференциальной форме или в векторном виде.
где J – плотность тока
Если участок цепи неоднородный, то в этом случае закон Ома имеет вид
ε 12- э.д.с. действующая на этом участке. В случае замкнутой цепи закон Ома имеет вид
где R - сопротивление всех проводников входящих в цепь, г - внутреннее сопротивление источника э.д.с. При прохождении по проводнику тока проводник нагревается. Экспериментально Джоуль и Ленц независимо друг от друга установили, что количество выделяющегося в проводнике тепла подчиняются следующему закону: Q =R I2 · t (9) где, R - сопротивление проводника, I -сила тока, t - время Для расчёта разветвленных цепей удобно пользоваться 1-м и 2-м правилом Кирхгофа. Первое правило Кирхгофа следует из закона сохранения заряда и гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:
Второе правило Кирхгофа следует из закона сохранения энергии и гласит, что алгебраическая сумма э.д.с включенных в замкнутую цепь, равна алгебраической сумме падений напряжений в данной цепи. Математически это записывается так:
где IR – падения напряжения, ε - э.д.с. Замкнутая электрическая цепь состоит из источника тока соединительных проводов и потребителя тока или нагрузка. При этом ток в цепи мы можем определить из закона Ома.
где R-сопротивление нагрузки, г - внутреннее сопротивление источника тока. Напряжение на нагрузке можно определить как
Работа, совершаемая в замкнутой цепи при, переносе заряда dq будет dA = ε-dq (14) Тогда мощность развиваемая: источником э.д.с., будет
В нагрузке выделяется только часть этой мощности
Эта мощность будет полезной. Остальная мощность расходуется в источнике тока и подводящих проводах. Отношение полезной мощности ко всей мощности, развиваемой э.д.с. определяет коэффициент полезного действия источника тока
Из этого выражения следует, что к.п.д. будет тем больше, чем больше сопротивление нагрузки R по сравнению с сопротивлением источника г. Переменный ток Переменным называют ток меняющийся как по величине (амплитуде) так и направлению. Квазистационарным называются токи, для которых их мгновенные значения во всех сечениях проводника (цепи) одинаковы. Условия квазистационарности: τ = Решения практических задач для переменного тока сводятся к нахождению амплитуды и мгновенных значений тока (напряжения), сдвига фаз между током и напряжением и полного сопротивлений. Мгновенное значение мощности, которое выделяется в цепи, будет: Pt = i(t) · u(t) = Im cos(ut - φ)Um cosωt (19) Используя формулу преобразования: сos α cosβ = получим
Практический интерес представляет среднее значения мощности по времени. Ток как среднее значение cos(2 ω t — φ) = 0, то
Действующее значение тока и напряжение находят по формулам: где φ - коэффициент мощности. 3. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ Собрать электрическую схему, где: 1- Источник тока Б5-8 2 - Сопротивление r =15 Ом. 3 - Амперметр, предел измерений до 1А 4 - RН – магазин сопротивлений Р14 RН 0 - 200 Ом 5 - Вольтметр, предел измерений 15В
1. Снять зависимость мощности источника тока от отношения сопротивления нагрузки Ru к внутреннему сопротивлению источника тока г (см. выражение (16). Построить график Р =f ( 2. Снять зависимость полезной мощности отношения сопротивления нагруз-ки RH к внутреннему сопротивлению источника тока r.(см. выражение (17) Построить график Рн =( 3. Снять зависимость КПД от отношения Rn к внутреннему сопротивлению источника тока r.(см. выражение (18). Построить график
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Электрический ток 2. Электродвижущая сила. 3. Закон Ома для однородного и неоднородного участка цепи. Закон Ома в дифференциальной форме. 4. Закон Джоуля – Ленца 5. Первое и второе правила Кирхгофа для разветвленной цепи. 6. Вывод формул для затраченной полезной мощности и коэффициент полезного действия источника тока. 7. Переменный ток. Мощность выделяем, в цепи переменного тока. Квазистационарные токи. Мгновенные и действующие значения тока и напряжения.
Работа № 15
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.247.59 (0.006 с.) |


 , (2)
, (2)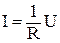 (3)
(3) (4)
(4)

 где ℓ- длина проводника, S - площадь поперечного сечения
где ℓ- длина проводника, S - площадь поперечного сечения где φ1 – φ2 - разность потенциалов на концах участка,
где φ1 – φ2 - разность потенциалов на концах участка,
 При этом узлом разветвления называется точка, в которой соединяются, как минимум, три проводника.
При этом узлом разветвления называется точка, в которой соединяются, как минимум, три проводника.

 ,
,
 или
или

 (18)
(18) << Т, где τ -время, необходимое для передачи электромагнитного возмущения в самую отдаленную точку цепи; L - длина цепи; c - скорость распространения электромагнитного возмущения (скорость света); Т- период колебания цепи. Для квазистационарных токов справедливы законы Ома и правила Кирхгофа, но в этом случае берутся мгновенные значения тока и напряжения.
<< Т, где τ -время, необходимое для передачи электромагнитного возмущения в самую отдаленную точку цепи; L - длина цепи; c - скорость распространения электромагнитного возмущения (скорость света); Т- период колебания цепи. Для квазистационарных токов справедливы законы Ома и правила Кирхгофа, но в этом случае берутся мгновенные значения тока и напряжения. cos(α - β) +
cos(α - β) + 
 , где соs φ =
, где соs φ =  , R - активное сопротивление цепи, Z - полное сопротивление цепи равная R+Хреактив=R +ХL
, R - активное сопротивление цепи, Z - полное сопротивление цепи равная R+Хреактив=R +ХL 
 , мощность нагрузки можно выразить через действующее значение тока и напряжения: Р=: Iq.Uq cos φ,
, мощность нагрузки можно выразить через действующее значение тока и напряжения: Р=: Iq.Uq cos φ, Рис.1
Рис.1 )
)



