
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение электрических затухающих колебанийСодержание книги
Поиск на нашем сайте 1. Цель работы: изучение характера затухающих электромагнитных колебаний и установление основных характеристик колебательного контура, определяющих процесс собственных колебаний
2. Теоретическая часть Электрическими колебаниями называются процессы периодического изменения зарядов или токов. Простейшей системой, в которой возможно длительное переменное движение зарядов и токов, является электрический колебательный контур. Колебательным контуром называется электрическая цепь, содержащая индуктивность и емкость (рис. 1) Собственные (свободные) колебания в контуре можно вызвать, либо сообщив обкладкам конденсатора некоторый начальный заряд, либо возбудив в индуктивности ток. Частота собственных незатухающих колебаний
называется собственной частотой контура. Для периода собственных колебаний получается так называемая формула Томсона:
Всякий реальный контур (рис 2) обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется на нагревание этого сопротивления и на излучение. Свободные колебания в реальном контуре, обладающем активным сопротивлением, будут затухающими. Метод описания электрических колебаний состоит в составлении и решении дифференциальных уравнений колебаний в соответствующих контурах. При этом основным уравнением для описания электромагнитных колебаний является закон Ома и вытекающее из него второе правило Кирхгофа. Решив дифференциальное уравнение, найдем тем самым закон конкретных колебаний.
Рис. 1 Рис. 2 Рассмотрим колебания в контуре с активным сопротивлением R (рис. 2). Применяя второе правило Кирхгофа для этого случая, имеем
откуда получаем дифференциальное уравнение реального колебательного контура в виде:
Здесь L,C, и R – соответственно индуктивность, емкость и сопротивление контура, а q – заряд конденсатора. Уравнение (4) приводится к стандартному виду:
путем следующей замены:
Величина
где Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону
а период затухающих колебаний контура
Затухание колебаний принято характеризовать коэффициентом затухания
откуда
то есть коэффициент затухания определяет убыль амплитуды за единицу времени. Логарифмическим декрементом (лат. «убавление») затухания называется величина
равная натуральному логарифму отношения двух последовательных амплитуд (11), разделенных во времени периодом колебаний Т. λ – величина безразмерная. Из формул (12) и (13) получаем
Из формул (6) и (14) с учетом того, что
Частота В зависимости от величины коэффициента затухания 1) 2) 3)
4)
Рис. 3 3. Экспериментальная часть Приборы и принадлежности. 1. Электронный осциллограф 2. Блок колебательного RLC контуры (L, C, магазин сопротивлений) Электрическая блок – схема установки представлена на рис. 4
Рис. 4 С генератора осциллографа (1) подается импульс тока, который заряжается конденсатор С, или С2. В колебательном контуре возникают собственные затухающие колебания, которые наблюдаем на экране осциллографа.
ВЫПОЛНЕНИЕ РАБОТЫ ЗАДАНИЕ 1. Определение логарифмического декремента затухания. 1. Смонтированный в коробке колебательный контур подключить к осциллографу по схеме (рис. 4) Установить значение сопротивления R = 0 и величину ёмкости С1 = 130пФ 2. После проверки схемы преподавателем (лаборантом) включить осциллограф и дать ему прогреться 2-3 мин. 3. Регулируя частоту развертки осциллографа и его синхронизацию, добиться получения на экране полной устойчивой картины затухающих колебаний, подобной рис. 3б. (затухание колебаний при R = 0 вызывают входные цепи осциллографа и сопротивление катушки). 4. Установить экспериментальную зависимость логарифмического декремента от сопротивления R, вводимого магазином: а) установить в контуре емкость С1 = 130пФ и сопротивление R = 0; определить по шкале на экране осциллографа величину амплитуды четырех последовательных полуразмахов Si электронного луча (рис. 5); результаты записать в таблицу 1; б) повторить пункт «а» для значения R = 200; 400; 600; 800; 1000 Ом; результаты записать в таблицу 1. 5. Повторить п. 4, установив емкость С2 = 750пФ; результаты записать в таблицу 1. 6. Во всех случаях рассчитать логарифмический декремент затухания по формуле:
результаты записать в таблицу 1. 7. В одних координатных осях построить два графика λ=λ(R) при значениях емкости С1 и С2 (п.4 и п.5). Сделать и записать в тетради вывод о зависимости логарифмического декремента от емкости С контура.
Рис. 5
ЗАДАНИЕ 2. Вычисление индуктивности катушки, собственной частоты контура и критического сопротивления. 1. По тангенсу угла наклона графиков λ=λ (R), построенных в задании 1, вычислить индуктивность катушки при емкостях С1 и С2 на основании формулы
где α – угол наклона кривых λ=λ (R), к оси абсцисс; результаты записать в таблицу 2; найти среднее значение индуктивности Lср. 2.Рассчитать собственную частоту контура по формуле
при Lср. найденном в п.1, и емкостях С1 и С2; результаты записать в таблицу 2. 3. Вычислить критическое сопротивление по формуле (16):
Таблица 1
Таблица 2
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Цель и производство работы. 2. Описание лабораторной установки. 3. Электромагнитные и гармонические колебания и их характеристики. 4. Принцип генерации электромагнитных колебаний в колебательном контуре. 5. Дифференциальное уравнение собственных электромагнитных колебаний. 6. Дифференциальное уравнение затухающих электромагнитных колебаний и их решение.
Библиографический список 2. Савельев И.В. Курс общей физики. Т.2.3 М.: Наука, 1982г.г. 3. Грабовский Р.И. Курс физики. М Высшая школа, 2002г. 4. 3.Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 1989г. 5. Калашников С.Г. Электричество. М.: Наука, 1977г.
Содержание
Гаврилова Анна Александровна, Гуриков Владимир Михайлович, Жиганов Александр Вениаминович,Краснов Александр Артемьевич, Резчиков Виктор Григорьевич, Хохолина Тамара Владимировна, Чурмасов Александр Васильевич
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ Учебное пособие
Редактор О.Ф Костина Корректор Т.Н. Калиниченко
Подписано в печать Формат 60х84 1/16 Печать офсетная. Печ. л. 11,2 Тираж 500 Заказ
Нижегородская государственная сельскохозяйственная академия 603107, г. Нижний Новгород, проспект Гагарина, 97 ______________________________________________________________ Типография НГСХА
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 (1)
(1) . (2)
. (2)

 , (3)
, (3) . (4)
. (4) (5)
(5)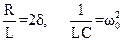 . (6)
. (6) называется коэффициентом затухания, ωо – собственная частота контура (1). Обе эти величины имеют размерность, обратную размерности времени. Общее решение уравнения (5) имеет вид:
называется коэффициентом затухания, ωо – собственная частота контура (1). Обе эти величины имеют размерность, обратную размерности времени. Общее решение уравнения (5) имеет вид: (7)
(7) . (8)
. (8) амплитудой колебания
амплитудой колебания  , зависящей от времени, и начальной фазой колебания φ. Частота затухающих колебаний контура (8) равна:
, зависящей от времени, и начальной фазой колебания φ. Частота затухающих колебаний контура (8) равна: (9)
(9) . (10)
. (10) , (11)
, (11)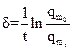 , (12)
, (12) , (13)
, (13) . (14)
. (14) , имеем
, имеем (15)
(15) (9), а следовательно, и
(9), а следовательно, и 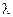 определяются параметрами контура L, C и R. Таким образом, логарифмический декремент затухания является характеристикой контура.
определяются параметрами контура L, C и R. Таким образом, логарифмический декремент затухания является характеристикой контура. из формулы (10)
из формулы (10)  - незатухающие колебания, определяемые согласно (7) уравнением
- незатухающие колебания, определяемые согласно (7) уравнением  , (рис.3а);
, (рис.3а); > 0: Т=
> 0: Т=  > Т0: заряд q совершает затухающие колебания (7) (рис. 3б);
> Т0: заряд q совершает затухающие колебания (7) (рис. 3б); ;
; 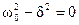 ; Т → ∞ - апериодический (критический) режим колебаний (рис. 3в); при этом критическое сопротивление контура может быть найдено с учетом (6) из соотношения:
; Т → ∞ - апериодический (критический) режим колебаний (рис. 3в); при этом критическое сопротивление контура может быть найдено с учетом (6) из соотношения: 
 . (16)
. (16)

 ;
;
 ,
,


