
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение баллистической постоянной гальванометраСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Включить освещение шкалы гальванометра. Установить нуль шкалы. 2. С помощью ключа К1 включить ток в цепи с нормальным соленоидом. При помощи реостата R установить силу тока 0,1 ампера. Включить ток в цепи с нормальным соленоидом. 3. Замкнуть ключ К2 в цепи с баллистическим соленоидом. 4. Замкнуть ключ К1 в цепи с нормальным соленоидом и замерить отброс «зайчика» (шкалы) α. После возвращения шкалы гальванометра в нулевое положение, разомкнуть ключ К2 и вновь отметить отброс шкалы гальванометра. Измерения повторить 2-3 раза. Из всех полученных данных вычислить среднюю величину отброса. 5. Пользуясь формулой (22), определить постоянную баллистического гальванометра для каждого измерения α. Из всех полученных значений вычислить среднее значение постоянной баллистического гальванометра. Результаты работы занести в таблицу 1.
ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ 6. Совместить плоскости обоих колец (А и В) земного индуктора и по компасу установить индуктор так, чтобы плоскости обоих колец были перпендикулярны плоскости магнитного меридиана. 7. При включенном токе в первичном соленоиде быстро повернуть за головку С весь индуктор на 180о, заметив при этом отброс «зайчика» (шкалы) β. Этот отсчет проделать 2-3 раза. Из всех полученных отбросов «зайчика» (шкалы) вычислить среднее значение величины β. 8. Пользуясь формулой (28) и (30), вычислить значение горизонтальной напряженности магнитного поля ЗемлиНВ. Результаты работы занести в таблицу 2.
ОПРЕДЕЛЕНИЕ ВЕРТИКАЛЬНОЙ СОСТАВЛЯЮЩЕЙ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
9. Совместить плоскости колец (А и В) земного индуктора и по компасу установить индуктор так, чтобы плоскости обоих колец были параллельны плоскости магнитного меридиана. 10. При включенном токе в первичном соленоиде быстро повернуть за головку Е – кольцо В на 90о, заметив при этом величину отброса «зайчика» (шкалы) γ. Опыт проделать 2-3 раза. Из величин всех полученных отбросов вычислить среднее значение величины γ. 11. Пользуясь формулой (16), вычислить значение вертикальной составляющей напряженности магнитного поля Земли НВ. 12. Пользуясь формулой (1), вычислить полное значение напряженности магнитного поля Земли Н.
Результаты работы занести в таблицу 3. Таблица 1 Определение постоянной баллистического гальванометра
Таблица 2 Определение горизонтальной составляющей напряженности поля земного магнетизма
Таблица 3 Определение вертикальной составляющей напряженности поля земного магнетизма.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Магнитное поле. Вектор магнитной индукции. 2. Закон Био – Савара- Лапласа и его применение для расчета магнитных полей. 3. Закон Ампера. Право левой руки. 4. Работа магнитного поля по перемещению проводника (контура) с током. 5. Явление электромагнитной индукции. Закон Фарадея и его вывод из закона сохранения энергии. Правило Ленца. Работа № 7 ГРАДУИРОВКА ТЕРМОПАРЫ 1. Цель работы:Ознакомиться термоэлектрическими явлениями и провести градуировку термопары.
Теоретическая часть В 1797 году Вольт открыл, что при соприкосновении двух различных металлов возникает некоторая разность потенциалов, называемая контактной разностью потенциалов. Причинами, вызывающими появление контактной разности потенциалов, являются следующие обстоятельства. 1. Различная работа выхода свободных электронов из различных металлов. Дело в том, что при обычных температурах электроны, совершая тепловое движение, не вырываются из металла; от вырывания из металла электроны удерживает как взаимодействие их с положительными зарядами остова кристаллической решетки, так и отталкивание внутрь металла со стороны тех электронов, которые ранее достигли поверхности металла. В результате, для выхода электрона из металла необходимо затратить вполне определенную, различную для разных металлов работу. При тесном контакте чистых поверхностей различных металлов работа выхода электронов за пределы своего металла несколько облегчается, но для разных металлов все же остается различной. Работа по перемещению электрического заряда в электрическом поле численно равна произведению перемещаемого электрического заряда на разность потенциалов тех точек поля, между которыми происходит перемещение заряда.
А = e(V − V0), где V − потенциал электрического поля внутри металла; а V0 − потенциал электрического поля вне металла. Практически потенциал вне металла равен нулю (V0=0), и формула работы по выходу электрона из металла принимает вид А= eV Тогда потенциал, который должен преодолеть электрон для выхода из металла(потенциал выхода) будет равен V= Таким образом, потенциал выхода численно равен работе, которую должен совершить электрон для того, чтобы выйти из данного металла. Пусть, например, при контакте двух металлов А и В работа выхода электронов из металла А будет меньше, чем работа выхода электронов из металла В. В этом случае потенциал выхода из металла А(VА) будет меньше потенциала выхода из металла В (VВ), и между металлами возникает контактная разность потенциалов.
причем металл А зарядится положительно, а металл В – отрицательно. 2. Различная концентрация свободных электронов в контактирующих металлах. Различные металлы отличаются своей структурой, а это влечет за собой и различное содержание свободных электронов в единице объема. Допустим, что концентрация свободных электронов в металле А больше, чем в металле В, т.е n0А>n0В. Вполне естественно, что из металла А будет по этой причине больше выходить электронов, чем из металла В; в результате между металлами А и В возникает разность потенциалов, причем металл А зарядится положительно, а металл В – отрицательно. Эта контактная разность потенциалов определяется формулой
где κ − постоянная Больцмана; Т – абсолютная температура места контакта.; е – заряд электрона; n0А, n0В – концентрация свободных электронов в металлах А и В. Таким образом, учитывая оба обстоятельства, вызывающие возникновение контактной разности потенциалов, можно написать:
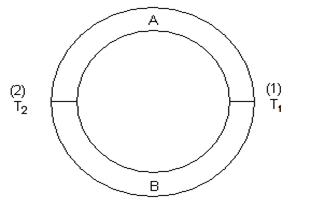
Следует при этом отметить, что эта электродвижущая сила будет наблюдаться лишь на концах разомкнутой цепи. В том случае, если последовательно соединенные различные металлы будут образовывать замкнутую цепь, то сумма контактных разностей потенциалов этих металлов будет равна нулю, так как контактные разности потенциалов на обоих контактах будут равны по величине и противоположны по знаку. Однако так будет обстоять дело лишь в том случае, если температура обоих контактов различных металлов одинакова. При разной температуре контактов в замкнутой цепи возникает электродвижущая сила, отличная от нуля; эта электродвижущая сила носит название термоэлектродвижущей силы. Допустим, что в замкнутой цепи, составленной из двух металлов А и В, контакт (1) поддерживается при температуре Т1, а контакт(23) при температуре Т2 (рис1)
Рис.1 Потенциалы выхода VА и VВ и концентрация свободных электронов n0А и n0В, вообще говоря, от температуры не зависят. Суммарная электродвижущая сила, возникающая в замкнутом контуре, может быть написана так:
Приведя подобные члены и переставив во втором логарифме числитель и знаменатель дроби, будем иметь:
Формула показывает, что электродвижущая сила, возникшая в замкнутом контуре при разной температуре контактов различных металлов прямопропорциональна разности температур этих контактов. Поскольку величины К, е, n0А и n0В являются постоянными, формула может быть преобразована в виде:
Е = с (Т1-Т2), (5) где
численно равна ЭДС, возникающая при изменении температуры контакта на 1оС. Хотя величина термоэлектродвижущей силы и невелика (несколько стотысячных долей вольта на 1о), термоэлектрические явления находят широкое применение как для измерения высоких температур, так и для обнаружения весьма слабых нагреваний. Для этого используются так называемые термоэлементы или термопары, которые представляют собой две проволоки из различных металлов с известной и заранее точно промеренной термоэлектродвижущей силой. В месте контакта проволоки свариваются. Один контакт помещается в среду с определенной постоянной температурой (То), а другой в среду, где изменяется температура (Т). Возникающая ЭДС измеряется при помощи вольтметра; по измеренной ЭДС определяется разность температур (Т –То); поскольку То заранее известна, находится и температура Т. Экспериментальная часть ОПИСАНИЕ ПРИБОРА Целью настоящей работы является градуировка термопары, т.е. установление зависимости термоэлектродвижущей силы от температуры (формула 4 и 5). Установка лабораторной работы состоит из следующих приборов: 1) термопара, 2)аккумулятор, 3) вольтметр, 4)гальванометр, 5) потенциометр, состоящий из двух магазинов сопротивления, 6) реохорд, 7) ключ, 8)сосуд Дюара, 9) электроплитка, 10) термометр. ВЫПОЛНЕНИЕ РАБОТЫ 1. Собрать электрическую цепь по приложенной схеме (рис.2)
Рис.2 При этом необходимо иметь ввиду, что: а) положительный полюс аккумулятора (+Е0) и положительный полюс термобатарей (+Т.Б) должны быть присоединены к одной и той же клемме реохорда (удобнее к той, около которой стоит нуль линейки), б) r1 – потенциометр с сопротивлением 240 Ом, r – потенциометр с сопротивлением 240 Ом,, r2 – реохорд с сопротивлением 7 Ом, в) отрицательный полюс термобатареи (-ТБ) через гальванометр должен быть подключен к подвижному контакту Р реохорда, г) левый спай термоэлемента опустить в сосуд Дюара, а правый – в стакан с холодной водой, поставленный на невключенную холодную электроплитку. В этот же стакан должен быть опущен термометр. 2. После проверки собранной цепи преподавателем поставить подвижной контакт Р реохорда на нулевое положение и включить рубильник К. Стрелка гальванометра должна стоять на нуле (в противном случае обратиться к преподавателю). 3. Записать показание термометра, включить электроплитку и наблюдать за изменением температуры. 4. Через каждые 5о нагрева: а) записать температуру, б) плавно, перемещая подвижной контакт Р, устанавливать стрелку гальванометра на нуль, в) записывать длину плеча реохорда от точки А до подвижного контакта Р.
5. Все эти измерения производить до температуры кипения воды или в случае до перемещения подвижного контакта реохорда до точки В. 6. Все измерения занести в 1,2,3,4 графы таблицы. Таблица
7. Для того чтобы вычислить ЭДС термобатареи (Е), а также величину С (термоэлектродвижущую силу, возникающую при изменении температуры нагреваемого спая на 1о), необходимо произвести некоторые теоретические расчеты и вычисления. Дело в том, что при том положении подвижного контакта Р, при котором стрелка гальванометра q будет стоять на нуле(ток отсутствует), термоэлектродвижущая сила будет в точности равна падению напряжения на участке реохорда от точки А до подвижного контакта Р. Поэтому прежде всего необходимо знать, каково падение напряжения на всем реохорде АВ, создаваемое аккумулятором Ео. Обозначим (см.рис.2) ток на потенциометре r1 через i1. на потенциометре r - через i и на реохорде r2 через i2; тогда, пользуясь первым законом Кирхгофа, можно написать для точки Д: i1+i2 =i (6) по второму закону Кирхгофа получается (для контура Ео Д Ео) i1 r1+ i r = V (7) Так как потенциометр r1 и реохорд r2 включены в цепь параллельно друг другу, то i1 r1= i2 r2 (8) Подставим в уравнение (7) вместо i его значение из уравнения (6). i1 r1+ i1 r+ i2 r = V (9) В уравнении (9) заменим i1 r1 через равную величину из равенства (8)
В последнем выражении вынести за скобку i2 r2
Так как i2 r2 = i1 r1, то выражение (11) может быть записано так:
Отсюда
i2 r2 – есть искомое напряжение на всем реохорде, создаваемое источником тока. 8. После того, как будет вычислено падение напряжения на всем реохорде, можно приступить к вычислению термоэлектродвижущей силы для каждой замеренной температуры (см.п.4 в разделе «Выполнение работы»). Порядок вычисления следующий: обозначим число всех делений реохорда через N; допустим, что для какого-нибудь наблюдения подвижной контакт остановился на n –ом делении реохорда и стрелка гальванометра стоит на нуле. Если при положении подвижного контакта Р на n –Ом делении реохорда стрелка гальванометра стоит на нуле- это означает, что термоэлектродвижущая сила, возникшая при данной температуре, компенсирует лишь ту часть напряжения на реохорде, которая приходится на часть реохорда, соответствующую n его делений (ЕФБ = VАР). Составим пропорцию: На N делений реохорда приходится i2 r2 вольт (см.форм.12), а на n делений придется х вольт.
Это напряжение х и есть электродвижущая сила (Е). которая возникла в термобатарее при некоторой зафиксированной температуре. Все эти расчеты термоэлектродвижущей силы занести в таблицу. 9. Вычислить для каждого номера наблюдения значение постоянной «с» по формуле (5). 10. Построить график зависимости термоэлектродвижущей силы от температуры, откладывая по оси абсцисс значение разности температур (tа - tв), а по оси ординат значение термоэлектродвижущей силы Е.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Цель и производство работы 2. Понятие о контактной разности потенциалов. Законы Вольты. 3. Термоэлектричество. ТермоЭДС и её применение в сельском хозяйстве. 4. Градуировка термопары. Работа № 8
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 614; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.243 (0.01 с.) |


 , (1)
, (1) , (2)
, (2) (3)
(3)

 (4)
(4) ,
,
 , см
, см
 ,В/К
,В/К
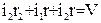 (10)
(10) (11)
(11)
 (12)
(12)
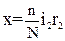 (13)
(13)


