
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение электрической емкости конденсатора баллистическим методомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КРАТКАЯ ТЕОРИЯ. Электрической емкостью называется физическая величина, показывающая заряд, который способно накапливать тело при приложении к нему потенциала в 1В:
Конденсатор – тело, способное накапливать достаточно большой заряд. Простейший конденсатор представляет собой два проводника (обкладки), разделенные слоем диэлектрика. Под электроемкостью конденсатора понимают физическую величину, показывающую заряд, который способен накапливать конденсатор при приложении к нему напряжения в 1 В.
Виды конденсаторов: 1. По электроемкости: конденсаторы постоянной емкости; конденсаторы переменной емкости. 2. По виду диэлектрика: воздушные; керамические; бумажные и т.д. 3. По форме обкладок: плоские; сферические и т. д. Конденсаторы соединяются в батареи. Виды соединения конденсаторов: А) последовательное; Б) параллельное.
где n – число конденсаторов. Для двух конденсаторов получим:
Общая электроемкость при параллельном соединении конденсаторов:
Как следует из (1), нахождение значения электроемкости связано с определением заряда Q на обкладках и напряжения U, которое определяется вольтметром V. Заряд Q можно измерить при помощи баллистического гальванометра. Главной частью гальванометра (рис. 2) является подвешенная на вертикальной нити Т рамка F, помещенная в поле постоянного магнита М. Скрепленное с рамкой зеркальце L служит для измерения угла поворота рамки гальванометра в магнитном поле при прохождении по ней электрического тока. Заряд Q, протекающий через рамку, пропорционален первому отбросу светового луча:
где А - постоянная гальванометра, N - число делений шкалы для первого отброса светового луча. Значение постоянной А можно определить, разряжая через гальванометр конденсатор известной ёмкости С, заряженный до напряжения U, тогда заряд конденсатоpa равен:
ИЗМЕРЕНИЯ. 1. Собрать схему (рис. 1), подключить конденсатор известной емкости и зарядить его до напряжения, при котором во время разряда конденсатора "зайчик" по шкале гальванометра отклонится на 0,7….0,8 длины шкалы. Далее, определив средний отброс "зайчика" из 5 опытов по разрядке известного конденсатора, найти постоянную гальванометра А, используя (4). 2. Определить емкости двух конденсаторов С1 и C2 по известной постоянной гальванометра А. Для этого подключают вместо образцового сначала конденсатор С1, потом C2. Изменяя напряжение на конденсаторе, добиться отклонения "зайчика" на 0,7...0,8 длины шкалы. Определив средний отброс "зайчика" из 5 опытов, находят значения емкостей C1 и C2 из формулы (4). 3. Определить емкость батареи из двух конденсаторов при параллельном и последовательном соединении. Сравнить результаты опыта с результатами вычисления емкости батареи по формулам (2) и (3). РЕЗУЛЬТАТЫ
ЛАБОРАТОРНАЯ РАБОТА № 4э ОПРЕДЕЛЕНИЕ ЭДС ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ МЕТОДОМ КОМПЕНСАЦИИ
Согласно закону Ома для полной цепи:
где e - ЭДС, i - сила тока, r - внутреннее сопротивление источника, U - напряжение на полюсах источника тока. Из формулы (1) видно, что обычные токопроводящие вольтметры непригодны для точного определения ЭДС. При отсутствии тока ЭДС равна напряжению на полюсах источника. Из этого следует, что принципиально возможно измерить ЭДС электростатическим или электронным вольтметром (вольтметрами, не потребляющими тока). Наиболее точным методом измерения ЭДС является метод компенсации. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Принципиальная схема компенсационного метода измерения ЭДС изображена на рис. 1. Вспомогательная батарея
Для того, чтобы исключить из уравнения (2) силу тока, вместо неизвестного элемента переключателем К подключают к цепи нормальный элемент Вестона (рис.1) с известной ЭДС Условие компенсации выразится равенством: Из (2) и (3) имеем: или
ЗАДАНИЕ. 1. Собрать схему (рис. 2) и поставить рукоятку тумблера К1 в такое положение, чтобы был включен элемент 2. Перекинуть рукоятку тумблера К1 и включить элемент
РЕЗУЛЬТАТЫ
ЛАБОРАТОРНАЯ РАБОТА № 6э ИЗУЧЕНИЕ ЗАВИСИМОСТИ МОЩНОСТИ ИСТОЧНИКА ТОКА ОТ СОПРОТИВЛЕНИЯ НАГРУЗКИ КРАТКАЯ ТЕОРИЯ. В электрической цепи, содержащей источник тока с ЭДС e и внутренним сопротивлением r, на резисторе R (рис.1) будет выделяться полезная мощность:
где I - сила тока. Согласно закону Ома для замкнутой цепи:
Из (1) и (2) следует что:
Ток I протекает так же и внутри источника, и поэтому в нем выделяется мощность
Полная мощность источника:
Полезная мощность источника
а затем убывает, стремясь к нулю при
ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ 1. Собрать цепь, состоящую из источника тока, ключа, магазина резисторов R согласно рис.1. 2. Снять зависимость тока I от сопротивления R. Результаты записать в виде таблицы. Изменение R с помощью декадных переключателей магазина производить при разомкнутом ключе. Ключ замыкается только на время проведения измерения. 3. Рассчитать полезную мощность по формуле (1) и вычертить график зависимости Рп (R). 4. По графику определить r, Pпmaх и, используя (6), рассчитать ЭДС источника тока e. ЛАБОРАТОРНАЯ РАБОТА № 13э
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 946; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.118 (0.007 с.) |

 .
. . (1)
. (1) Общая емкость при последовательном соединении конденсаторов:
Общая емкость при последовательном соединении конденсаторов: ,
, . (2)
. (2) . (3)
. (3)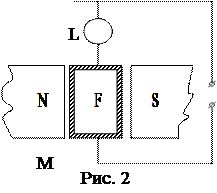 ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для определения емкости конденсатора пользуются схемой, приведенной на рис.1, где ИП - источник постоянного напряжения, V - вольтметр, Сх - исследуемый конденсатор, Кн - переключатель, позволяющий подключать конденсатор к источнику питания или к гальванометру Г. Параллельно гальванометру подключен ключ Кл, который замыкают на короткое время перед измерением для установки светового луча ("зайчика") в начальное положение.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для определения емкости конденсатора пользуются схемой, приведенной на рис.1, где ИП - источник постоянного напряжения, V - вольтметр, Сх - исследуемый конденсатор, Кн - переключатель, позволяющий подключать конденсатор к источнику питания или к гальванометру Г. Параллельно гальванометру подключен ключ Кл, который замыкают на короткое время перед измерением для установки светового луча ("зайчика") в начальное положение. ,
, ,
, 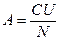 и
и 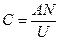 . (4)
. (4) КРАТКАЯ ТЕОРИЯ. При протекании электрического тока в замкнутой цепи, состоящей из проводника и источника тока (электрической батареи), оказывается, что внутри источника тока положительные заряды должны перемещаться против сил электростатического поля. Это возможно только в том случае, если на заряды действуют силы неэлектрического происхождения, так называемые сторонние силы. Работа сторонних сил по перенесению 1 Кл заряда между теми точками цепи, где они действуют, называется электродвижущей силой (ЭДС):
КРАТКАЯ ТЕОРИЯ. При протекании электрического тока в замкнутой цепи, состоящей из проводника и источника тока (электрической батареи), оказывается, что внутри источника тока положительные заряды должны перемещаться против сил электростатического поля. Это возможно только в том случае, если на заряды действуют силы неэлектрического происхождения, так называемые сторонние силы. Работа сторонних сил по перенесению 1 Кл заряда между теми точками цепи, где они действуют, называется электродвижущей силой (ЭДС):  . ЭДС измеряется в вольтах.
. ЭДС измеряется в вольтах.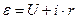 , (1)
, (1) с ЭДС, заведомо превосходящей ЭДС исследуемого элемента, поддерживает ток в цепи реохорда АВ0. Исследуемый источник ЭДС
с ЭДС, заведомо превосходящей ЭДС исследуемого элемента, поддерживает ток в цепи реохорда АВ0. Исследуемый источник ЭДС  одним полюсом присоединен к точке А, а другим - через гальванометр G и сопротивление R к движку реохорда D. Компенсация ЭДС
одним полюсом присоединен к точке А, а другим - через гальванометр G и сопротивление R к движку реохорда D. Компенсация ЭДС  (сопротивлением Rx), чтобы напряжение на нем равнялось
(сопротивлением Rx), чтобы напряжение на нем равнялось  ). В уравновешенной таким образом цепи согласно закону Кирхгофа для контура AD
). В уравновешенной таким образом цепи согласно закону Кирхгофа для контура AD  . (2)
. (2) . Компенсация ЭДС произойдет при новом положении движка (при длине AD равной lN и сопротивления этого участка RN).
. Компенсация ЭДС произойдет при новом положении движка (при длине AD равной lN и сопротивления этого участка RN). . (3)
. (3) (4)
(4) . (5)
. (5) Таким образом, измерение ЭДС сводится к измерению длин участков реохорда. В рассматриваемом методе гальванометр применяется не для измерения тока, а для констатации его отсутствия. Для этих целей применяются приборы, у которых нуль расположен посередине шкалы. Точность измерения ЭДС по схеме на рис. 1 невелика, так как при отсчете длины делаются погрешности более 0,5 мм. Кроме того, в процессе эксплуатации проволока стирается, и ее сопротивление по длине делается неоднородным. Монтажная схема установки изображена на рис. 2. Сопротивление R (порядка 104 Ом) служит для ограничения тока, текущего через гальванометр. Нормальный и исследуемый элемент подключаются к схеме с помощью ключа К2. В опытах батарея
Таким образом, измерение ЭДС сводится к измерению длин участков реохорда. В рассматриваемом методе гальванометр применяется не для измерения тока, а для констатации его отсутствия. Для этих целей применяются приборы, у которых нуль расположен посередине шкалы. Точность измерения ЭДС по схеме на рис. 1 невелика, так как при отсчете длины делаются погрешности более 0,5 мм. Кроме того, в процессе эксплуатации проволока стирается, и ее сопротивление по длине делается неоднородным. Монтажная схема установки изображена на рис. 2. Сопротивление R (порядка 104 Ом) служит для ограничения тока, текущего через гальванометр. Нормальный и исследуемый элемент подключаются к схеме с помощью ключа К2. В опытах батарея 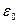 , элементы
, элементы 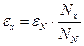 рассчитать ЭДС. Опыты повторить с вторым элементом и обоими элементами, включенными последовательно. Результат представить в виде:
рассчитать ЭДС. Опыты повторить с вторым элементом и обоими элементами, включенными последовательно. Результат представить в виде: .
. , (1)
, (1)
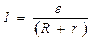 . (2)
. (2) . (3)
. (3) .
. . (4)
. (4) изменяется от нуля при R = 0, проходит через максимум при
изменяется от нуля при R = 0, проходит через максимум при , (5)
, (5) . Максимальное значение полезной мощности:
. Максимальное значение полезной мощности: . (6)
. (6)


