
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение фокусных расстояний линзСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прямая, проходящая через центры кривизны сферических поверхностей линзы, называется главной оптической осью (рис. 1). Если одна из поверхностей линзы плоская, то оптическая ось проходит перпендикулярно к ней. Точки пересечения поверхностей линзы с главной оптической осью (рис. 1, точки O1, О2) называются вершинами. Расстояние между вершинами называется толщиной линзы. Линза называется тонкой, если ее толщина значительно меньше радиусов кривизны ее поверхностей. Точка тонкой линзы, через которую лучи проходят без изменения своего направления, называется оптическим центром линзы. Главная оптическая ось проходит через оптический центр. Любая другая прямая, проходящая через оптический центр линзы, называется побочной осью линзы. Линза называется собирающей, если она преобразует падающий на нее параксиальный пучок лучей, параллельный главной оптической оси, в сходящийся гомоцентрический пучок. В противном случае линза называется рассеивающей.
У любой линзы имеется два фокуса. Расстояние от оптического центра тонкой линзы до фокуса называется фокусным расстоянием. Плоскости, проходящие через фокусы перпендикулярно главной оптической оси, называются фокальными плоскостями. Если среда по обе стороны линзы одна и та же, то модули ее фокусных расстояний равны. Для параксиальных пучков лучей, которые преобразуются тонкой линзой, выполняется соотношение
где a1 — расстояние от линзы до предмета, a2 — расстояние от линзы до изображения, f — фокусное расстояние линзы, R1 и R2 — радиусы кривизны сферических поверхностей, ограничивающих линзу, n — относительный показатель преломления вещества, из которого изготовлена линза. Соотношение (1) называется формулой тонкой линзы. Правило знаков. При расчетах по формуле (1) значения a1 или а2 подставляются со знаком плюс, если направления их отсчета от оптического центра линзы совпадают с направлением распространения света (см. рис. 2). Значения R1 и R2 также подставляются со знаком плюс, если их направления отсчета от вершин сферических поверхностей совпадают с направлением распространения света, в противном случае эти значения подставляются со знаками минус. Радиус кривизны R1 относится к той поверхности линзы, которая первой пересекается светом. Значения фокусного расстояния f собирающей линзы подставляются со знаком плюс, рассеивающей — со знаком минус. Отношение показателя преломления окружающей линзу среды к ее фокусному расстоянию называется оптической силой:
Единица оптической силы — диоптрия (дптр). 1 диоптрия — это оптическая сила линзы, расположенной в воздухе, с фокусным расстоянием 1 м. Оптическая сила — величина алгебраическая: собирающая линза имеет положительную оптическую силу, рассеивающая — отрицательную. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для определения фокусных расстояний используется оптическая скамья, на которой с помощью рейтеров устанавливаются освещённое матовое стекло с прямоугольной сеткой, белый экран и соответствующие линзы. Определение фокусного расстояния собирающей линзы
2-й способ. Если расстояние A между сеткой и экраном будет больше 4 f, то посредством перемещения линзы при данном расстоянии A можно получить два изображения предмета - увеличенное и уменьшенное - (рис. 3). В этом случае уравнение (1) можно представить в следующем виде: Два корня этого уравнения a′1 и a′′1 соответствуют двум возможным положениям линзы относительно сетки. На рис. 3 указаны эти положения линзы и соответствующие построения изображений, большему значению a1 (по модулю) соответствуют штриховые линии. Если обозначить разность ЗАДАНИЕ. Измерить двумя способами фокусное расстояние собирающей линзы.
ЛАБОРАТОРНАЯ РАБОТА №5о
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.41.252 (0.008 с.) |

 КРАТКАЯ ТЕОРИЯ. Линзой называется прозрачное для оптического излучения тело, у которого две противоположные стороны ограничены криволинейными поверхностями. Одна из поверхностей может быть плоской. Наибольшее применение имеют линзы со сферическими поверхностями.
КРАТКАЯ ТЕОРИЯ. Линзой называется прозрачное для оптического излучения тело, у которого две противоположные стороны ограничены криволинейными поверхностями. Одна из поверхностей может быть плоской. Наибольшее применение имеют линзы со сферическими поверхностями. Точка на главной оптической оси, в которой пересекаются параксиальные лучи, параллельные главной оптической оси собирающей линзы, называется фокусом. В рассеивающей линзе параксиальный пучок лучей, параллельный главной оптической оси, преобразуется в расходящийся пучок, продолжения этих лучей пересекаются в точке, лежащей на главной оптической оси. Эта точка называется фокусом рассеивающей линзы.
Точка на главной оптической оси, в которой пересекаются параксиальные лучи, параллельные главной оптической оси собирающей линзы, называется фокусом. В рассеивающей линзе параксиальный пучок лучей, параллельный главной оптической оси, преобразуется в расходящийся пучок, продолжения этих лучей пересекаются в точке, лежащей на главной оптической оси. Эта точка называется фокусом рассеивающей линзы. , (1)
, (1) . (2)
. (2) 1-й способ. Перемещением линзы и экрана добиваются получения чёткого изображения сетки на экране. Измеряется расстояние a2 между линзой и экраном. Измеряются линейные размеры сетки y1 и линейные размеры её изображения y2. Находится фокусное расстояние f по формуле:
1-й способ. Перемещением линзы и экрана добиваются получения чёткого изображения сетки на экране. Измеряется расстояние a2 между линзой и экраном. Измеряются линейные размеры сетки y1 и линейные размеры её изображения y2. Находится фокусное расстояние f по формуле: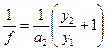 .
.
 , то получится расчётная формула:
, то получится расчётная формула:  . В этом способе измеряется расстояние между сеткой и экраном А и расстояние l.
. В этом способе измеряется расстояние между сеткой и экраном А и расстояние l.


