
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение горизонтальной составляющейСодержание книги
Поиск на нашем сайте МАГНИТНОЙ ИНДУКЦИИ ЗЕМЛИ МЕТОДОМ ГАУССА КРАТКАЯ ТЕОРИЯ. Для характеристики магнитных свойств замкнутых токов вводят величину, называемую магнитным моментом тока. Магнитный момент тока есть вектор, направление которого совпадает с направлением положительной нормали к плоскости витка стоком (рис. 1). Если
где i - сила тока, S - площадь контура с током i.
что иллюстрируется рис. 2б.
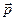 часто называют магнитным диполем. часто называют магнитным диполем.
Возьмем магнит в форме призматического стержня и подвесим его на тонкой и длинной нити так, чтобы он занимал горизонтальное положение (рис. 3). Магнит устанавливается в направлении магнитного меридиана (упругость нити пренебрежимо мала). Если стержень вывести из положения равновесия (в горизонтальной плоскости), то на него будет действовать согласно формуле (3) вращающий момент:
где BЗ.Г — горизонтальная составляющая индукции магнитного поля Земли, а φ — угол отклонения от положения равновесия. Под воздействием механического момента возникнут крутильные колебания. Пренебрегая трением и упругостью нити, можно записать:
где I -момент инерции магнита. При малых углах:
Введя подстановку
Уравнение (5) –дифференциальное уравнение гармонических колебаний. Его решение имеет вид:
где φ0 – амплитуда колебаний, w - циклическая частота. Период колебаний равен:
Момент инерции призматического магнита относительно оси, проходящей через центр тяжести перпендикулярно к его длине, вычисляется по формуле
где l -длина магнита; a - его ширина; m - масса магнита. В уравнение (7) входит еще неизвестная величина р. Поставим второй опыт, который позволит найти связь между BЗ.Г и р в конечном счете искомую величину BЗ.Г без определения р. Возьмем скамью со шкалой и с помощью буссоли, прикрепленной на ее конце, установим ее параллельно магнитному меридиану. После этого возьмем магнит (который должен подвешиваться на нити) и расположим его на скамье так, как это показано на рис. 4.
где BМ — индукция поля, создаваемая постоянным магнитом в месте расположения буссоли. Принимая α =900, из (2) найдем:
Исключая из уравнений (7) и (10) величину p и учитывая (9), получим:
Для определения BЗ.Г в последнюю формулу следует подставить измеренные значения r, T, tg β и вычисленное значение I. Чтобы исключить ошибку, зависящую от несовпадения магнитной оси буссоли с ее геометрической осью, угол отсчитывают от обоих концов стрелки. Для исключения ошибки на неточность установления буссоли магнит поворачивают около вертикальной оси на 180° и повторяют измерение угла β. Из четырех полученных значений находят среднее, которым пользуются в дальнейших вычислениях. ЗАДАНИЕ 1.Скамью расположить так, как показано на рис. 4 (скамья располагается параллельно магнитному меридиану). 2. Измерить величины, необходимые для вычисления горизонтальной составляющей индукции магнитного поля Земли по формулам (8) и (11). 3. Результаты вычислений усреднить.
ЛАБОРАТОРНАЯ РАБОТА № 2o ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА КРАТКАЯ ТЕОРИЯ. Интерференцией волн называется процесс наложения волн, при котором происходит их взаимное усиление или ослабление. Интерферировать могут волны любой природы, в том числе и электромагнитные (в частности световые). Устойчивое чередование интерференционных минимумов и максимумов интенсивности (интерференционная картина) наблюдается в случае соблюдения условий когерентности волн: 1. Совпадение частот источников волн. 2. Постоянство разности фаз интерферирующих волн во времени. 3. Одинаковая поляризация интерферирующих волн. При освещении однородной плоскопараллельной пластинки светом разность хода волн, отраженных от верхней и нижней плоскостей, зависит от углов падения и толщины пластинки. Если на пути отраженных лучей установить собирающую линзу, то устойчивая интерференционная картина будет наблюдаться на экране, расположенном в её фокальной плоскости. Поскольку точки фокальной плоскости линзы сопряжены бесконечно удаленным,то говорят, что интерференционная картина локализована в бесконечности. Отметим, что в данном случае устойчивая интерференционная картина образуется параллельными лучами, отраженными от пластинки. Наблюдаемые на экране полосы названы полосами равного наклона. При освещении пластинки (например, клина) параллельным пучком лучей разность хода лучей, отраженных от верхней и нижней поверхностей пластинки зависит от толщины пластинки. Ввиду непараллельности поверхностей отраженные лучи пересекутся на конечном расстоянии от отражающих плоскостей, и интерференционная картина будет локализована вблизи пластинки. Поскольку в этом случае разность хода определяется лишь толщиной пластинки, то для ее точек, соответствующих одинаковому расстоянию между отражающими поверхностями, условия максимумов и минимумов неизменны. Такие интерференционные полосы называются полосами равной толщины. В данной работе исследуются полосы равной толщины, которые возникают в результате интерференции волн, отраженных от границы прослойки между сферической поверхностью линзы и поверхностью плоской пластинки. Интерференционные полосы, возникающие в этой системе, имеют вид концентрических окружностей (колец). Они называются кольцами Ньютона. При нормальном падении лучей и большом радиусе кривизны поверхности линзы можно пренебречь различием в углах падения лучей на сферическую поверхность. Тогда разность хода волн
По рис. 1 имеем:
Темные кольца (минимум освещенности) образуются при условии:
Из (4) и (5) радиусы темных (rm) и светлых (rc) колец:
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 759; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |

 есть единичный вектор вдоль нормали, то магнитный момент тока
есть единичный вектор вдоль нормали, то магнитный момент тока 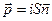 , (1)
, (1)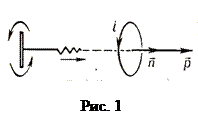 Существуют постоянные магниты, магнитное поле которых создается молекулярными токами. Поле прямолинейного магнита подобно полю соленоида (рис. 2а).
Существуют постоянные магниты, магнитное поле которых создается молекулярными токами. Поле прямолинейного магнита подобно полю соленоида (рис. 2а). Полосовой магнит характеризуется некоторым магнитным моментом
Полосовой магнит характеризуется некоторым магнитным моментом  , (2)
, (2)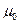 =4p×10-7 Гн/м - магнитная постоянная
=4p×10-7 Гн/м - магнитная постоянная
 (3)
(3) , (4)
, (4) ,
,
 запишем:
запишем: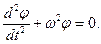 (5)
(5) (6)
(6) (7)
(7) (8)
(8)
 , (9)
, (9)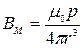 . (10)
. (10) 
 (11)
(11)  будет определяться только толщиной зазора:
будет определяться только толщиной зазора: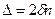 . (1)
. (1) . (2)
. (2)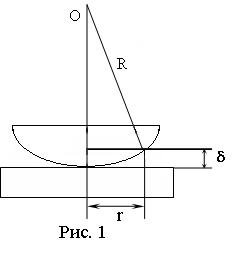 Необходимо учесть, что при отражении от границы раздела стекло-воздух фаза вектора
Необходимо учесть, что при отражении от границы раздела стекло-воздух фаза вектора  не изменяется, в то время как при отражении от границы воздух-стекло происходит потеря половины длины волны, поэтому разность хода интерферирующих лучей в отраженном свете (для n = 1) будет равна:
не изменяется, в то время как при отражении от границы воздух-стекло происходит потеря половины длины волны, поэтому разность хода интерферирующих лучей в отраженном свете (для n = 1) будет равна: . (3)
. (3) (4)
(4) Светлые кольца образуются при условии:
Светлые кольца образуются при условии: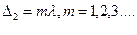
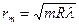 , (6)
, (6)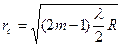 . (7)
. (7)


