
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение показателя преломления рефрактометромСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КРАТКАЯ ТЕОРИЯ. Луч (cветовой луч) — геометрическая линия, вдоль которой распространяется энергия, переносимая электромагнитными волнами. Законы геометрической оптики можно использовать в том случае, когда площадь фронта волны значительно больше произведения b l (b — расстояние от линзы до точки наблюдения, l — длина волны). Закон прямолинейного распространения света в однородной среде: в однородной среде лучи являются прямыми линиями. Углом падения называется угол между направлением падающего луча и перпендикуляром к границе раздела в точке падения. Угол между этим перпендикуляром и направлением отраженного луча называется углом отражения. Закон отражения. Падающий и отраженный лучи и перпендикуляр к поверхности в точке падения лежат в одной плоскости. При падении луча на границу раздела двух изотропных сред угол отражения равен углу падения. В зависимости от свойств границы раздела различают два вида отражения света. Если поверхность раздела имеет неровности, размеры которых значительно меньше длины волны света, то происходит зеркальное отражение. В этом случае падающие параллельные лучи света после отражения остаются параллельными. Если неровности расположены на отражающей поверхности хаотично и имеют размеры, сравнимые с длиной волны, то происходит диффузное отражение. В этом случае параллельные лучи света после отражения перестают быть параллельными, однако при условии Угол между перпендикуляром к границе раздела сред в точке падения луча и направлением преломленного луча называется углом преломления. Закон преломления (для изотропных сред). Падающий и преломленный лучи, перпендикуляр в точке падения лежат в одной плоскости. При преломлении светового луча на границе раздела двух данных изотропных сред отношение синуса угла падения к синусу угла преломления есть величина постоянная для данной длины волны:
где n – относительный показатель преломления второй среды относительно первой – физическая величина, равная отношению скоростей света в соответствующих средах:
Показатель преломления среды относительно вакуума называется абсолютным показателем преломления среды.
При переходе из среды, оптически более плотной, в среду, оптически менее плотную, луч может полностью отражаться. Это явление называется полным отражением. Угол падения iпр, начиная с которого свет полностью отражается от границы раздела, называется предельным углом полного отражения. Он определяется из соотношения:
где n определяется формулой (1). c2 – скорость света в оптически более плотной среде. Оптические приборы, предназначенные для измерения показателя преломления, называются рефрактометрами.
При измерениях используются два метода: метод скользящего луча и метод полного отражения. Метод скользящего луча. Свет направляется через грань АВ призмы Р1, проходит через матовую поверхность АС и далее через слой жидкости проникает в призму P2. Для лучей, которые скользят вдоль грани, можно записать закон преломления в виде:
где
Преломляющий угол призмы
Учитывая (1), (2), (3), найдем:
Угол выхода лучей
Метод полного отражения. Свет вводится в рефрактометр через матовую грань DF призмы Р2. Свет падает на эту грань под всевозможными углами. При углах падения При освещении призм белым светом граница раздела будет размыта и окрашена в различные цвета из-за дисперсии в призме Р2. Чтобы получить резкое изображение, перед объективом зрительной трубы помещаются две призмы прямого зрения (призмы Амичи) (см. 6 на рис.2). Каждая призма состоит из трех склеенных призм с различными показателями преломления и дисперсией (например, крайние призмы изготовлены из кронгласа, средняя - из флинтгласа). Призмы рассчитаны так, чтобы монохроматический луч с длиной волны 5893 ангстрем не испытывал отклонения. Такое устройство называется компенсатором. При положении призм компенсатора, указанном на рис.2, их дисперсия равна нулю. При повороте одной из призм на 180° дисперсия будет равна удвоенному значению дисперсии одной призмы (при равных дисперсиях обоих призм). В зависимости от взаимной ориентации дисперсию можно изменять от нуля до максимального значения. Поворотом призм компенсатора с помощью специального устройства (см.10 на рис.3) добиваются резкого изображения границы, положение которой соответствует значению показателя преломления желтой линии натрия (5893 ангстрем). В простых конструкциях рефрактометров в качестве компенсатора используется одна призма. Общий вид рефрактометра показан на рис. 3. Обозначения те же, что на рис. 2. Для удобства измерений шкала отградуирована в значениях показателя преломления. В указанной конструкции рефрактометра имеется два окна, что позволяет вести измерения обоими способами. Для установки компенсатора служит барабан 10. В оправе призм сделана камера, через которую может прокачиваться жидкость для поддержания постоянной температуры. Подача термостатирующей жидкости осуществляется через штуцеры 11. ЗАДАНИЕ. 1. Перед началом работы необходимо проверить установку прибора. С этой целью между призмами 2 и 3 помещается капля дистиллированной воды. Смещая окуляр в тубусе трубы, добиваются четко изображения шкалы и визирной линии. Поворотом компенсатора добиваются четкого изображения границы. Зрительную трубу перемещают до совпадения визирной линии с границей раздела. При правильной установке прибора показание на нем должно быть 1.333 (при 20°С). 2. Измерить показатели преломления раствора сахара в воде для трех различных концентраций. Измерения провести обоими способами, рассмотренными выше. Измерение каждого значения проводится 3 раза. Рассчитать среднее значение и оценить погрешность измерений. РЕЗУЛЬТАТЫ
ЛАБОРАТОРНАЯ РАБОТА №11о ИССЛЕДОВАНИЕ АТОМАРНОГО СПЕКТРА ВОДОРОДА КРАТКАЯ ТЕОРИЯ. Спектры изолированных атомов линейчатые, т.е. излучение сосредоточено вблизи некоторых определенных длин волн. Линейчатый спектр, полученный с помощью призмы в диапазоне видимого излучения, представляет собой тонкие линии, имеющие различную окраску. Количество линий и расположение их по шкале длин волн характерны для данного газа. Положение линии спектра атомов водорода определяется соотношением (в видимой части спектра):
где n = 3, 4, 5,....; Rv - постоянная Ридберга. Эти линии относятся к серии Бальмера. Соотношение (1) сначала было получено экспериментальным путем, затем объяснено полуклассической моделью Резерфорда-Бора, которая основана на двух постулатах. Первый постулат - условие стационарных орбит. В атоме электроны движутся по стационарным круговым или эллиптическим орбитам; в центре круговой орбиты находится ядро; при движении по стационарным орбитам электрон не излучает энергии. Стационарные круговые орбиты определяются условием:
mе- масса электрона, Второй постулат - условие частот. Излучение или поглощение атомом кванта энергии происходит тогда, когда электрон переходит с одной стационарнойорбиты на другую; при таких переходах излучается или поглощается фотон, энергия которого
где En1 и En2 - уровни энергии, соответствующие стационарным орбитам. На основе постулатов Бора можно рассчитать энергетические уровни стационарных состояний водородоподобных ионов и атомов водорода. Из решения уравнения движения электрона (в атоме водорода):
с учетом (2) и (3) следует, что энергия стационарных состояний атома водорода
частота излучения
где n 1 < n2, n1и n2имеют целочисленные значения,
В серии Бальмера для первых четырех линий значения Более строгое решение задачи по определению энергетических уровней стационарных состояний проводится на основе уравнения Шредингера. Из решения следует, что для определения стационарных состояний атома необходимы, кроме главного квантового числа, еще два квантовых числа: орбитальное квантовое число l, которое определяет механический момент импульса электрона Квантовые числа связаны между собой: ℓ может иметь значения от 0 до Полный момент импульса электрона в атоме водорода
где j - внутреннее квантовое число, которое может иметь значения ℓ+s;│ℓ-s│; состояниям с различными j соответствуют различные значения энергии, в результате происходит расщепление каждого уровня на два (тонкая структура спектральных линий). Не расщепляются лишь уровни ℓ =0, так как в этом случае j имеет единственное значение j= 1/2.
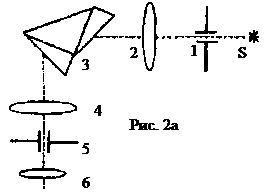
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Используется универсальный монохроматор (УМ-2) (рис. 2а). От источника S через входную щель 1 свет проходит к объективу коллиматора 2, после чего направляется на систему призм 3 и в зрительную трубу (объектив 4, окуляр 6).
ЗАДАНИЕ. 1. Измерить длины волн спектральных линий водорода, используя градуировочную кривую. Следует обратить внимание, что в спектре водородной трубки наблюдается спектр молекулярного водорода. Начинать измерение лучше всего с красной линии Нα; вторая линия Hβ - зелено-голубая. В промежутках между Нα и Hβ наблюдается система слабых молекулярных полос. Третья линия Нγ - фиолетово-синяя. Перед этой линией имеются две слабые молекулярные полосы синего цвета. Четвертая линия Hδ -фиолетовая; она наблюдается лишь в некоторых экземплярах трубок. 2. Рассчитать постоянную Ридберга.
ЛАБОРАТОРНАЯ РАБОТА №16о ИЗУЧЕНИЕ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ КРАТКАЯ ТЕОРИЯ. Название «лазер» происходит от начальных букв английского выражения (усиление света за счет вынужденного излучения). Лазер, как и любой генератор, состоит из трех основных частей: резонансной системы, обратной связи и источника энергии. В качестве резонансной системы используют два параллельных зеркала; собственные частоты такого резонатора зависят от расстояния между зеркалами. Условие резонанса состоит в том, что между зеркалами укладывается целое число полуволн электромагнитного излучения. Обратная связь обеспечивается вынужденным (индуцированным) излучением возбужденной атомарной или молекулярной среды. Энергия источника расходуется на это возбуждение. Взаимодействие электромагнитного излучения с веществом осуществляется тремя способами: 1) атомы поглощают квант энергии и переходят на более высокий уровень; 2) возбужденные атомы могут спонтанно излучать кванты и переходить в низшее энергетическое состояние; 3) возбужденные атомы могут излучать кванты под действием поля излучения той же частоты. Последний процесс называется вынужденным (или индуцированным) излучением. Особенность вынужденного излучения состоит в том, что частота, фаза, поляризация и направление распространения индуцированного фотона совпадает с соответствующими характеристиками стимулирующего излучения. Вынужденное излучение используется для возбуждения резонатора, который должен быть настроен на частоту перехода в атомной системе. Для получения вынужденного излучения необходимо, чтобы концентрация атомов n2, находящихся на лазерном уровне, была больше концентрации атомов n1 в невозбужденном состоянии. Такое соотношение между n1 и n2 отсутствует в условиях теплового равновесия, когда имеет место закон распределения Больцмана
где hν - энергия кванта, k - постоянная Больцмана, T - абсолютная температура. При комнатных температурах в оптическом диапазоне отношение: Скорость убывания количества возбужденных атомов в единичном объеме n2, за счет спонтанных и вынужденных переходов, определяется уравнением Эйнштейна:
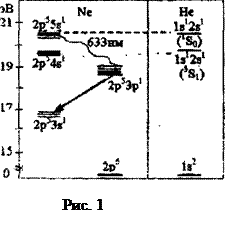
где A (2,1) - вероятность спонтанного перехода с уровня 2; B (2,1) – вероятность вынужденного перехода с уровня 2 на уровень 1 в поле с частотой v12 и плотностью излучения ρ(v12); B (1,2) - вероятность возбуждения атомов с уровня 1 на уровень 2; B (2,1) = В (1,2). Для возбуждения колебаний в резонаторе необходимо, чтобы потери энергии потока квантов за один проход между зеркалами были меньше усиления за счет вынужденного излучения. Создание инверсной заселенности уровней (n 2>> n 1) осуществляется различными способами; к ним относятся столкновения второго рода, оптическая накачка, рекомбинация в плазме, химические реакции в газах и др. В гелий - неоновом лазере используются столкновения первого и второго рода, в рубиновых лазерах – оптическая накачка. Столкновения первого рода происходят в большинстве случаев между электронами газового разряда и атомами, находящимися в основном состоянии: е + х → x* + е; звездочка означает возбужденное состояние. Этот процесс соответствует неупругому столкновению электрона и атома.
Схема уровней неона и гелия приводится на рис. 1. Возбуждение атомов гелия производится соударением первого рода. Путем соударений второго рода между атомами гелия в состоянии ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Лазер (рис. 2) состоит из газоразрядной трубки 3, подогревного катода 5 и анода 4. На торцах трубки расположены выходные окна 2, установленные под углом Брюстера по отношению к оси трубки. Вследствие этого излучение поляризуется перпендикулярно плоскости падения (направление Газоразрядная трубка помещается в оптический резонатор, состоящий из двух зеркал 1, 6 с многослойными диэлектрическими покрытиями; одно зеркало плоское с коэффициентом отражения 98% и коэффициентом пропускания 1%, другое – сферическое с коэффициентом отражения 99%. Наличие сферического зеркала (с радиусом 120 см) упрощает настойку резонатора. Ориентация зеркал и расстояние между ними устанавливается специальными микрометрическими винтами; при правильной юстировке зеркал вынужденное излучение направляется вдоль оси газоразрядной трубки, в результате чего обеспечивается исключительная направленность лазерного излучения.
Экспериментальная установка представлена на рис.3. На оптической скамье 1 типа ОСК-2 неподвижно закреплен газовый лазер 2. Луч лазера распространяется параллельно направляющим оптической скамьи. На перемещающихся рейтерах в зависимости от выполняемого задания устанавливаются: вращающийся поляроид 3, пластинка 4, дифракционная решетка 5, экран 6, который может перемещаться в вертикальном и горизонтальном направлениях.
2. Измерить длину волны излучения с помощью дифракционной решетки. Измеряется на экране линейное отклонение
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.192.214 (0.011 с.) |

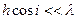 (h — размеры неровностей; i — угол падения лучей) отраженные лучи становятся почти параллельными, т. е. отражение можно считать зеркальным.
(h — размеры неровностей; i — угол падения лучей) отраженные лучи становятся почти параллельными, т. е. отражение можно считать зеркальным.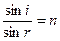 ,
,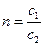 . (1)
. (1)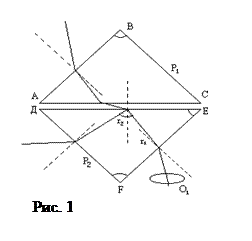 Показатель преломления среды относительно вакуума называется абсолютным показателем преломления среды. Показатель преломления среды зависит от длины волны падающего света (или его частоты). Среда, в которой скорость света больше называется оптически менее плотной, иначе – оптически более плотной.
Показатель преломления среды относительно вакуума называется абсолютным показателем преломления среды. Показатель преломления среды зависит от длины волны падающего света (или его частоты). Среда, в которой скорость света больше называется оптически менее плотной, иначе – оптически более плотной.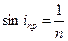 ,
,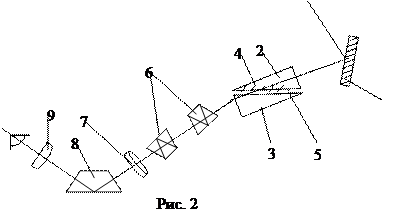 Определение показателя преломления можно проводить различными способами: по измерению углов падения и преломления, по измерению наименьшего угла отклонения призмы и её преломляющего угла, интерференционными методами (по смещению интерференционных полос), по смещению изображения предмета, рассматриваемого через плоскопараллельную пластинку с помощью микроскопа, иммерсионными методами и методами, основанными на полном отражении. В работе применяется рефрактометр Аббэ. Исследуемая среда (обычно жидкость) помещается в зазоре (около 0.1 мм) между гранями двух стеклянных прямоугольных призм (рис. 1).
Определение показателя преломления можно проводить различными способами: по измерению углов падения и преломления, по измерению наименьшего угла отклонения призмы и её преломляющего угла, интерференционными методами (по смещению интерференционных полос), по смещению изображения предмета, рассматриваемого через плоскопараллельную пластинку с помощью микроскопа, иммерсионными методами и методами, основанными на полном отражении. В работе применяется рефрактометр Аббэ. Исследуемая среда (обычно жидкость) помещается в зазоре (около 0.1 мм) между гранями двух стеклянных прямоугольных призм (рис. 1).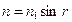 , (1)
, (1) равен предельному углу отражения для границы стекло - исследуемое вещество,
равен предельному углу отражения для границы стекло - исследуемое вещество, 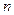 - показатель преломления исследуемой среды в зазоpe;
- показатель преломления исследуемой среды в зазоpe; 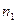 - показатель преломления стекла призмы (
- показатель преломления стекла призмы (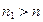 ).Для грани ЕF закон преломления записывается в виде:
).Для грани ЕF закон преломления записывается в виде: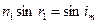 . (2)
. (2) (3)
(3) . (4)
. (4) будет иметь наименьшее значение для скользящих лучей. Лучи, проходящие через грань EF, будут выходить под углами от 90° до
будет иметь наименьшее значение для скользящих лучей. Лучи, проходящие через грань EF, будут выходить под углами от 90° до  На рис. 2 представлен схематически ход лучей в рефрактометре Аббе: 1 - осветительное зеркало, 2 – откидная призма, 3 - основная призма, 4 – матовая грань, 5 - исследуемое вещество, 6 - призмы компенсатора, 7 - объектив трубы, 8 - оборотная призма, 9 - окуляр с отсчетной шкалой, расположенный в фокальной плоскости окуляра. Граница рассматривается через вторую линзу, которая совместно с О1 образует зрительную трубу, установленную на бесконечность. С помощью такой трубы определяется угол
На рис. 2 представлен схематически ход лучей в рефрактометре Аббе: 1 - осветительное зеркало, 2 – откидная призма, 3 - основная призма, 4 – матовая грань, 5 - исследуемое вещество, 6 - призмы компенсатора, 7 - объектив трубы, 8 - оборотная призма, 9 - окуляр с отсчетной шкалой, расположенный в фокальной плоскости окуляра. Граница рассматривается через вторую линзу, которая совместно с О1 образует зрительную трубу, установленную на бесконечность. С помощью такой трубы определяется угол  и
и  рассчитывается показатель преломления.
рассчитывается показатель преломления. будет наблюдаться полное отражение. Лучи, проходящие через грань EF и имеющие угол выхода
будет наблюдаться полное отражение. Лучи, проходящие через грань EF и имеющие угол выхода 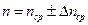 , где
, где 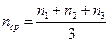 - среднее значение показателя преломления,
- среднее значение показателя преломления,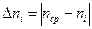 - отклонение данного измерения от среднего значения,
- отклонение данного измерения от среднего значения,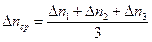 - среднее значения абсолютной погрешности.
- среднее значения абсолютной погрешности.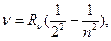 (1)
(1)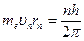 , (2)
, (2)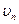 - его линейная скорость,
- его линейная скорость, 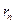 - радиус стационарной орбиты, h- постоянная Планка, n- 1,2,3,... -квантовое число. Первый постулат находится в противоречии с классическими законами электродинамики.
- радиус стационарной орбиты, h- постоянная Планка, n- 1,2,3,... -квантовое число. Первый постулат находится в противоречии с классическими законами электродинамики.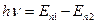 , (3)
, (3)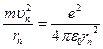 , (4)
, (4)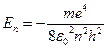 , (5)
, (5)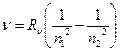 , (6)
, (6)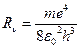 - постоянная Ридберга (для частот). Схема дискретных энергетических уровней, соответствующая соотношению (5), представлена на рис. 1.
- постоянная Ридберга (для частот). Схема дискретных энергетических уровней, соответствующая соотношению (5), представлена на рис. 1.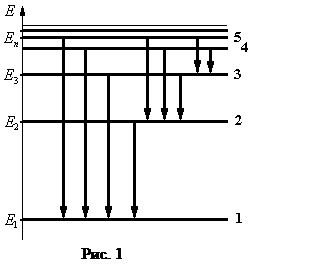 При переходе электронов в атоме водорода на уровень с наименьшей энергией
При переходе электронов в атоме водорода на уровень с наименьшей энергией 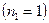 излучается серия линий, которые находятся в ультрафиолетовой части спектра (серия Лаймана); при переходах на уровень с квантовым числом
излучается серия линий, которые находятся в ультрафиолетовой части спектра (серия Лаймана); при переходах на уровень с квантовым числом 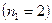 излучаются линии серии Бальмера (четыре линии этой серии лежат в видимой части) и т.д. (см. рис. 1).
излучаются линии серии Бальмера (четыре линии этой серии лежат в видимой части) и т.д. (см. рис. 1).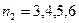 . Эти линии обозначаются
. Эти линии обозначаются 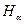 ,
, 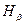 ,
, 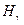 ,
, 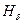 и обычно используются в экспериментах.
и обычно используются в экспериментах.
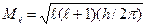 ; магнитное квантовое число m, определяющее ориентацию момента импульса в пространстве, т.е. проекцию вектора
; магнитное квантовое число m, определяющее ориентацию момента импульса в пространстве, т.е. проекцию вектора 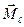 на направление внешнего магнитного поля;
на направление внешнего магнитного поля; 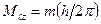 . Электрон также обладает собственным моментом импульса
. Электрон также обладает собственным моментом импульса 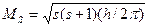 , где s – спиновое квантовое число.
, где s – спиновое квантовое число.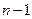 , m - от - ℓ..., 0,... до ℓ; s имеет одно значение, равное 1/2 (для электрона). В квантовой механике орбиты не представляют истинного движения электронов; движение электрона описывается на основе его волновых свойств уравнением Шредингера. Однако представление о стационарных уровнях энергии атома и в квантовой механике сохраняется.
, m - от - ℓ..., 0,... до ℓ; s имеет одно значение, равное 1/2 (для электрона). В квантовой механике орбиты не представляют истинного движения электронов; движение электрона описывается на основе его волновых свойств уравнением Шредингера. Однако представление о стационарных уровнях энергии атома и в квантовой механике сохраняется.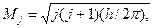
 При переходе электрона с одного энергетического уровня на другой квантовое число ℓ может изменяться на ±1 (правило отбора), что соответствует закону изменения импульса.
При переходе электрона с одного энергетического уровня на другой квантовое число ℓ может изменяться на ±1 (правило отбора), что соответствует закону изменения импульса.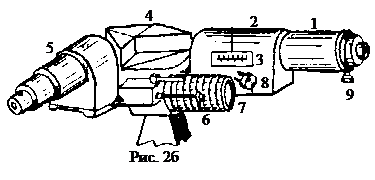 На рис. 2б приводится внешний вид монохроматора. Коллиматор 1 закреплен в обойме 2. Входной щелью коллиматора является стандартная симметричная щель, ширина которой изменяется в пределах от 0 до 4 мм с помощью винта 9. Фокусировка объектива производится с помощью маховика 8; положение объектива определяется по шкале, расположенной в окне 3. Призменный столик 4 поворотным механизмом приводит микрометрического винта. На барабане имеются относительные деления - градусы; отсчет производится по указателю 6, скользящему по спиральной канавке. Зрительная труба 5 смонтирована во второй обойме. Шкала барабана и окна освещаются специальными осветителями.
На рис. 2б приводится внешний вид монохроматора. Коллиматор 1 закреплен в обойме 2. Входной щелью коллиматора является стандартная симметричная щель, ширина которой изменяется в пределах от 0 до 4 мм с помощью винта 9. Фокусировка объектива производится с помощью маховика 8; положение объектива определяется по шкале, расположенной в окне 3. Призменный столик 4 поворотным механизмом приводит микрометрического винта. На барабане имеются относительные деления - градусы; отсчет производится по указателю 6, скользящему по спиральной канавке. Зрительная труба 5 смонтирована во второй обойме. Шкала барабана и окна освещаются специальными осветителями.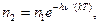 (1)
(1)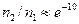 . Чтобы n2 было больше n1, необходимо создать неравновесную систему; для этого требуется затрата энергии.
. Чтобы n2 было больше n1, необходимо создать неравновесную систему; для этого требуется затрата энергии.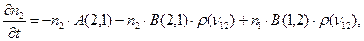 (2)
(2) Столкновения второго рода происходят в смеси двух газов, в которых энергия метастабильного уровня атомов одного газа близка к энергии возбужденного уровня атомов другого газа: X + Y* → Y + X*. Этот процесс соответствует неупругому столкновению двух атомов, при этом энергия с метастабильного уровня одного атома передается на возбужденный уровень атомов другого газа. Вероятность соударений второго рода имеет значительную величину только тогда, когда энергии возбуждения уровней близки.
Столкновения второго рода происходят в смеси двух газов, в которых энергия метастабильного уровня атомов одного газа близка к энергии возбужденного уровня атомов другого газа: X + Y* → Y + X*. Этот процесс соответствует неупругому столкновению двух атомов, при этом энергия с метастабильного уровня одного атома передается на возбужденный уровень атомов другого газа. Вероятность соударений второго рода имеет значительную величину только тогда, когда энергии возбуждения уровней близки.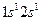 и атомами неона в состоянии
и атомами неона в состоянии 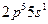 , создается инверсная заселенность уровня
, создается инверсная заселенность уровня 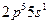 . При вынужденных переходах между уровнями неона
. При вынужденных переходах между уровнями неона 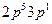 возникает генерация на линии неона с длиной волны λ=632.8 нм. Переходы с уровня
возникает генерация на линии неона с длиной волны λ=632.8 нм. Переходы с уровня 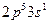 ; последний разгружается вследствие соударений со стенками разрядной трубки.
; последний разгружается вследствие соударений со стенками разрядной трубки.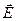 перпендикулярно плоскости падения). Активной средой в трубке является газ, состоящий из смеси гелия (парциальное давление около 100 Па) и неона (около 10 Па).
перпендикулярно плоскости падения). Активной средой в трубке является газ, состоящий из смеси гелия (парциальное давление около 100 Па) и неона (около 10 Па).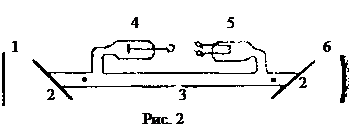 Гелий-неоновый лазер питается от высоковольтового источника постоянного напряжения (1.6 - 2.5 кВ). Вынужденное излучение лазера, в отличие от возникающего в нем спонтанного излучения, имеет значительно большую временную и пространственную когерентность, а также обладает острой угловой направленностью светового луча и большей мощностью излучения.
Гелий-неоновый лазер питается от высоковольтового источника постоянного напряжения (1.6 - 2.5 кВ). Вынужденное излучение лазера, в отличие от возникающего в нем спонтанного излучения, имеет значительно большую временную и пространственную когерентность, а также обладает острой угловой направленностью светового луча и большей мощностью излучения.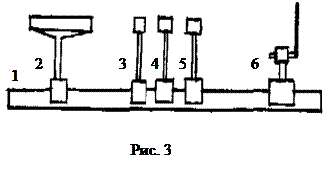 ЗАДАНИЕ. 1. Измерить угол расхождения лазерного пучка. С этой целью экран размещается вблизи выходного отверстия лазера и измеряется диаметр пятна d 1; затем экран перемещается на расстояние L (2-4 м) и вновь измеряется диаметр пятна d 2. Угловое расхождение пучка
ЗАДАНИЕ. 1. Измерить угол расхождения лазерного пучка. С этой целью экран размещается вблизи выходного отверстия лазера и измеряется диаметр пятна d 1; затем экран перемещается на расстояние L (2-4 м) и вновь измеряется диаметр пятна d 2. Угловое расхождение пучка 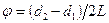 . Сравнить полученное значение φ с дифракционным расширением пучка, рассчитанным по соотношению
. Сравнить полученное значение φ с дифракционным расширением пучка, рассчитанным по соотношению 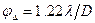 , где D - эффективный диаметр пучка на выходе из лазера.
, где D - эффективный диаметр пучка на выходе из лазера.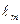 спектра m -го порядка от спектра нулевого порядка и расстояние от решетки до экрана; рассчитывается угол дифракции из соотношения
спектра m -го порядка от спектра нулевого порядка и расстояние от решетки до экрана; рассчитывается угол дифракции из соотношения 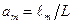 , а затем длина волны.
, а затем длина волны.


