
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Искусственное двулучепреломлениеСодержание книги
Поиск на нашем сайте
где k – коэффициент пропорциональности, зависящий от свойств вещества. Поместим стеклянную пластинку Q между скрещенными поляризаторами Р и Р' (рис.3.9). Пока стекло не деформировано, такая система свет не пропускает. Если же стекло подвергнуть деформации (например, одностороннему сжатию), свет через систему начинает проходить, причем наблюдаемая в прошедших лучах картина будет испещрена цветными полосами. Каждая такая полоса соответствует одинаково деформированным местам пластинки. Следовательно, по характеру расположения полос можно судить о распределении напряжений внутри пластинки. На искусственном двойном лучепреломлении основывается оптический метод исследования напряжений. Изготовленная из прозрачного изотропного материала (например, из целлулоида или плексигласа) модель какой-либо детали или конструкции помещается между скрещенными поляризаторами. Модель подвергается действию нагрузок, аналогичных тем, какие будет испытывать само изделие. Наблюдаемая при этом в проходящем белом свете картина позволяет определить распределение напряжений, а также судить об их величине. Возникновение оптической анизотропии в прозрачных телах под нагрузкой называется фотоупругостью. Объектом исследования может служить любая прозрачная пластмассовая деталь со стенками или линейка, коробка от аудиокассеты. При наблюдении в скрещенных поляроидах можно наблюдать красивые цветные узоры. Эти узоры обычно сгущаются вблизи углов и кромок, швов и отверстий, где есть остаточные напряжения. Методика измерений а) Определение степени поляризации частично поляризованного света
Связь между качеством неидеального поляроида и степенью поляризации Р света, прошедшего через такой поляроид, можно установить из определения (3.10) степени поляризации
откуда
Пусть естественный свет проходит через два одинаковых неидеальных поляроида. При параллельной ориентации их оптических осей составляющая естественного света, параллельная оптической оси обоих поляроидов, пройдёт без изменения:
а перпендикулярная будет ослаблена в
Полная интенсивность света, измеренная прибором, поставленным после прохождения светом двух неидеальных одинаковых поляроидов, равна их сумме (эти две составляющие некогерентны):
При перпендикулярной ориентации оптических осей двух одинаковых поляроидов составляющая естественного света, параллельная оптической оси первого поляроида, проходит через первый без изменения, и ослабляется вторым в К раз:
а перпендикулярная будет ослаблена только первым тоже в
Полная интенсивность света равна их сумме:
Отношение интенсивностей при параллельной и перпендикулярной ориентации оптических осей:
Величина n измеряется экспериментально. Уравнение (3.21) можно решить относительно K:
По определению K>1, тогда знак минус в (3.22) надо исключить. Итак,
Затем можно рассчитать степень поляризации света, прошедшего через один поляроид:
и через два параллельных поляроида:
Очевидно, закон Малюса для неидеальных одинаковых поляроидов примет вид (3.24)
При б) Интерференция поляризованных лучей. Определение степени анизотропии
Оптическая разность хода Δ равна разности оптических длин путей обыкновенного и необыкновенного лучей:
Отсюда разность фаз между обоими лучами равна
где Пусть на анизотропную пластинку падает линейно поляризованный белый свет. Длины волн белого света имеют всевозможные значения в интервале приблизительно 380÷780 нм. Получающаяся в кристалле разность хода для лучей одних длин волн будет равна четному, для других – нечетному числу полуволн. Поэтому волны одних длин будут при интерференции уничтожаться, другие, наоборот, усиливаться. В результате отношение интенсивностей различных цветов будет иным, чем в белом свете, и кристалл будет казаться окрашенным. Каждой разности хода соответствует некоторая интерференционная окраска. Интерференционные окраски не являются чистыми монохроматическими спектральными цветами, но представляют собой смесь в различных пропорциях всех цветов, входящих в состав белого, кроме тех, которые уничтожаются при данной разности хода. Наблюдение и исследование интерференционных цветов имеет очень большое значение в кристаллооптической методике. Познакомиться с цветами, получающимися при различных разностях хода. В таблице Мишеля-Леви (рис.3.11) последовательно отображаются переходы интерференционных цветов, наблюдаемые при изменении толщины образца.
Экспериментальная часть
Старая установка (установка № 1) Приборы и оборудование: установка, включающая осветитель, фотоэлемент, два поляроида, микроамперметр. Описание установки № 1 Схема установки показана на рис.3.12. В корпусе основания помещена лампа накаливания 1, закрытая стеклом. На верхней панели основания размещены микроамперметр 2 для регистрации фототока, ручка регулировки величины фототока 3 и тумблер включения установки. На нижнем столике находится поляроид 4, служащий поляризатором. На верхнем столике установлен поляроид 5 с лимбом для отсчета углов, играющий роль анализатора. Фотоэлемент 6 служит для регистрации интенсивности света, прошедшего через поляроиды. Внимание! Из-за недостаточно высокого быстродействия фотоприемника снятие показаний микроамперметра нужно производить не ранее, чем через 10 секунд после поворота поляроида. Ввиду использования в данной работе пленочных поляроидов, характерным недостатком которых является селективность поглощения при разных длинах волн, излучение лампы, прошедшее через поляризатор, не будет иметь степень поляризации 100%, т.е. будет частично поляризовано. Новая установка ( установка № 2) Приборы и оборудование: установка, включающая осветитель и два поляроида, люксметр, исследуемые образцы: полимерная плёнка разной толщины, закреплённая между пластинами из оргстекла; модель балки из оргстекла. Описание установки № 2
Порядок выполнения работы Задание 1. Определение степени поляризации частично поляризованного света (рекомендуется сделать на обеих установках).
Внимание! Все измерения проводятся при выключенном верхнем освещении. Установка № 1 1. Включите электропитание установки. 2. Выведите фотоприемник из светового луча, сместив его влево, и введите в пучок света свободное отверстие. 3. Установите риску анализатора 5 (рис.3.12) против цифры "90" на лимбе. Вращая поляризатор, добейтесь максимального затемнения (поляроиды скрещены). 4. Введите в луч света фотоприемник 6 и измерьте значение фототока I min, запишите в табл.3.1. 5. Вращая поляризатор, найдите положение, соответствующее минимальной силе тока и ещё раз её измерьте. Всего сделайте не менее 3 измерений I min, рассчитайте среднее значение. 6. Переведите анализатор в положение "0". Убедитесь, что фототок максимален. Сделайте не менее трёх измерений; среднее значение максимального фототока I max запишите в таблицу 3.1. 7. Найдите n и K по формулам (3.21) и (3.23).
8. Найдите степени поляризации света, прошедшего через один поляроид и через два параллельных поляроида по формулам (3.22) и (3.23).
9. Выключите установку № 1. Установка № 2 1. Включите электропитание установки. 2. Установите поляризатор 1 на «0», анализатор 2 на «900» (рис.3.13). При этом их главные плоскости скрещены. 3. Приготовьте люксметр к работе: поставьте фотоэлемент 3 на анализатор 2 и нажмите левую кнопку (30 – 300 – 3.103 – 3.104) блока индикации 4. При этом показания следует снимать по нижней шкале. Внимание! Блок индикации должен быть установлен строго горизонтально на ровной поверхности. 4. Поверните до упора по часовой стрелке регулятор накала 5. 5. Придерживая снизу стекло анализатора 2 и поворачивая его, найдите положения, соответствующие минимальной и максимальной интенсивности света. 6. Сделайте не менее трёх измерений I min и I max, в табл.3.1 запишите средние значения. 7. Вычислите K, P 1 и P 2. 8. Сравните степени поляризации света для обеих установок. Сделайте выводы.
Таблица 3.1
Задание 2. Количественная проверка закона Малюса. 1. На установке № 2 установите поляризатор 1 и анализатор 2 на «0», при этом их оптические оси параллельны. Вращая поляризатор 1, изменяйте угол φ между оптическими осями поляризатора и анализатора от 0 до 900 с интервалом 100, измеряйте освещённость I экс., запишите в табл.3.2. 2. Вычислите теоретическое значение для каждого угла
3. В одних и тех же координатных осях постройте графики зависимости теоретических I теор. и экспериментальных I экс. значений освещённости от угла φ: I теор= f (φ) и I экс= f (φ). 4. Сделайте выводы.
Таблица 3.2
Задание 3. Определение степени анизотропии 1. Уберите люксметр. 2. Скрестите поляризатор и анализатор (поле зрения тёмное, поляризатор установлен на «0», анализатор – на «900»). 3. Установите между ними пластинку. 4. Поворачивая пластинку, добейтесь наиболее яркой интерференционной картины. 5. По таблице Мишеля-Леви определите оптическую разность хода для полимерной плёнки: однослойной, двухслойной и трёхслойной. 6. Определите степень анизотропии
Таблица 3.3
7. Запишите все данные в табл.3.3. Задание 4. Наблюдение фотоупругости. 1. Поставьте поляроиды в скрещенное положение. 2. Введите в пучок света модель балки. Зарисуйте наблюдаемую картину, объясните. В процессе выполнения задания можно изменить нагрузку на балку. 3. Опишите явление, объясните. 4. Между скрещенными поляроидами поместите любую прозрачную пластмассовая деталь или линейку. 5. Опишите явление, объясните, почему цветные узоры сгущаются вблизи углов и кромок, швов и отверстий. Контрольные вопросы 1. Что представляет собой электромагнитная волна? 2. Что такое плоско (или линейно) поляризованный свет? Какая плоскость называется плоскостью поляризации? Плоскостью колебаний? 3. Чем естественный свет отличается от поляризованного? 4. Возможна ли поляризация продольных волн? 5. Как можно получить линейно поляризованный свет? 6. Сформулируйте и выведите закон Малюса. 7. Какой свет называется эллиптически поляризованным? Поляризованным по кругу? 8. В чем заключается явление двойного лучепреломления? Как оно объясняется? 9. Как поляризованы обыкновенный и необыкновенный лучи? 10. Что такое главная плоскость кристалла? 11. Что такое дихроизм? 12. Как можно создать искусственную анизотропию? Где она применяется? Используемая литература [1] §§ 30.1, 34.1, 34.2, 34.4; [2] § 26.1; [3] §§ 3.31, 3.46, 3.47; [5] §§ 98, 100, 101; [7] §§ 190-195. Лабораторная работа 3-04 Вращение плоскости поляризации Цель работы: изучение принципа работы поляриметров, определение удельного вращения кварца и раствора сахара, определение концентрации сахара в растворе. Теоретическое введение Свет является поперечной электромагнитной волной. Естественный свет представляет собой совокупность волн, излучаемых множеством атомов независимо друг от друга. Поэтому естественный свет не поляризован. Если же направления колебаний светового вектора Поляризованный свет можно получить из естественного с помощью поляризатора (призма Николя, поляроид и др.). Он пропускает колебания, параллельные только одной (главной) плоскости, и полностью задерживает колебания, перпендикулярные этой плоскости. Чтобы исследовать, является ли свет после прохождения поляризатора действительно плоско-поляризованным, на пути лучей ставят второй поляризатор, который называют анализатором. Пусть колебания вектора
где Если главные плоскости поляризатора и анализатора параллельны (φ=0, π; cosφ=±1), то экран, помещенный за анализатором, будет максимально освещенным. Если φ=π/2, т.е. cosφ=0 (поляризатор и анализатор скрещены), то экран будет темным. Среди явлений, возникающих при взаимодействии света с веществом, важное место и в принципиальном, и в практическом отношении занимает явление, открытое Д. Араго в 1811 г. при изучении двойного лучепреломления в кварце: при прохождении поляризованного света через некоторые вещества наблюдаетсявращение плоскости поляризации. Такие вещества называются оптически активными. К их числу относятся кристаллические тела (кварц, киноварь и др.), чистые жидкости (скипидар, никотин и др.) и растворы некоторых веществ (водные растворы сахара, винной кислоты и др.). Измерение вращения плоскости поляризации стало популярным аналитическим методом в ряде промышленных областей. Кристаллические вещества, например, кварц, сильнее всего вращают плоскость поляризации в случае, когда свет распространяется вдоль оптической оси кристалла. Угол поворота φ пропорционален пути l, пройденному лучом в кристалле: φ =α l. (4.3) Коэффициент α называют постоянной вращения. Для растворов Ж.Био (1831 г.) обнаружил следующие закономерности: угол φ поворота плоскости поляризации пропорционален пути l луча в растворе и концентрации С активного вещества в растворе: φ =[α] Сl, (4.4) где [α] – удельное вращение. Оно характеризует природу вещества, зависит от природы вещества и температуры. Удельное вращение обратно пропорционально квадрату длины волны: При 20°С и λ=589 нм удельное вращение сахара равно: [α]=66.5 град.см3/(г.дм)=0.665 град.м2/кг. Постоянная вращения кварца для жёлтых лучей (λ=589 нм): α=21.7 град/мм, а для фиолетовых (λ=404.7 нм) α=48.9 град/мм. Исследования показали, что объяснение явления вращения плоскости поляризации света в естественно-активных веществах можно получить, рассматривая общую задачу взаимодействия электромагнитной световой волны с молекулами или атомами веществ, если только принять во внимание конечные размеры молекул и их структуру. Эта задача очень сложна. В свое время О.Френель (1817 г.) представил описание этого явления, сведя его к особому типу двойного лучепреломления. В основе рассуждений Френеля лежит гипотеза, согласно которой скорость распространения света в активных веществах различна для волн, поляризованных по левому и по правому кругу. Представим плоско-поляризованную волну как суперпозицию двух волн, поляризованных по кругу вправо и влево с одинаковыми амплитудами и периодами. Если оба вектора
Кроме того, физиологическое и биохимическое действие оптических изомеров часто совершенно различно. Так, в живой природе белки строятся из левых оптических изомеров аминокислот (19 из 20 жизненно важных аминокислот оптически активны). Белки, синтезированные искусственным путём из правых аминокислот, не усваиваются организмом; а левый никотин в несколько раз ядовитее правого. Удивительный феномен преимущественной роли только одной из форм оптических изомеров в биологических процессах может иметь фундаментальное значение для выяснения путей зарождения и эволюции жизни на Земле.
Экспериментальная часть Приборы и оборудование: поляриметр, кюветы с растворами сахара. Описание установки
Часть стенки корпуса 6 прибора может перемещаться, открывая доступ во внутреннюю часть корпуса, куда поочередно помещают трубки с исследуемыми растворами сахара.
Источником света в сахариметре является лампа накаливания Л. Свет от лампы падает на фильтр Ф и объектив О. Полученный монохроматический свет проходит через поляризатор П, кювету Т с раствором и анализатор А. В качестве поляризатора и анализатора в приборе используются поляроиды. После анализатора свет проходит через объектив Об и окуляр Ок зрительной трубы сахариметра, которая служит для визуального наблюдения поля зрения. Вследствие адаптации глаза визуально трудно оценивать абсолютную освещенность. В то же время легко сравнивать освещенность различных частей поля зрения. Для разделения поля зрения на части в сахариметре непосредственно за поляризатором расположена тонкая кварцевая пластинка К, через которую проходит средняя часть пучка поляризованного света, вышедшего из поляризатора. В результате введения кварцевой пластинки поле зрения сахариметра оказывается разделенным на три части. Средняя часть освещается светом, прошедшим через поляризатор, кварцевую пластинку и анализатор, а две крайние части поля зрения – светом, прошедшим через поляризатор и анализатор. Так как кварц является оптически активным веществом, то после прохождения поляризованного света через пластинку его плоскость поляризации поворачивается на некоторый угол (рис. 4.6,а).
В одном случае яркость поля зрения будет больше, в другом – меньше. При работе с сахариметром следует уравнивать части поля зрения при меньшей яркости.
Порядок выполнения работы
Задание 1. Определение удельного вращения сахара 1. Включите осветитель сахариметра в сеть. 2. Установите окуляр 5 на ясное видение разделяющих линий тройного поля зрения. 3. Добейтесь равномерного затемнения трех частей поля зрения, вращая кремальеру 4. При этом шторка на трубке прибора должна быть закрыта. 4. Снимите отсчет n0 по шкале прибора. Измерение повторите три раза: n'0, n0'', n0''' и найдите n0 ср. 5. Измерьте и запишите в табл.4.2 длину l трубки 1 с раствором сахара известной концентрации C 1. 6. Поместите трубку 1 в сахариметр и, перемещая окуляр 5, восстановите фокусировку. 7. Снова добейтесь равномерного затемнения трех частей поля зрения. Снимите отсчет n. 8. Измерения повторите три раза: n', n", n'" и найдите n ср; 9. Определите угол вращения плоскости поляризации: j=n ср- n0 ср. (4.5) 10. Определите удельное вращение раствора сахара (4.4). 11. Результаты измерений и вычислений занесите в таблицу 4.2. 12. Сравните полученное значение удельного вращения с табличным.
Таблица 4.1
Таблица 4.2
Задание 2. Определение концентрации раствора сахара 1. Поместите в сахариметр трубку 2 с раствором сахара неизвестной концентрации С 2 и, повторив операции п. 2÷9 задания 1, определите угол вращения 2. Вычислите концентрацию С 2неизвестного раствора сахара по формуле (4.4), используя полученное в задании 1 значение [a]. 3. Определите погрешность концентрации Δ С 2. 4. Данные измерений и вычислений занесите в таблицу 4.3. 5. Повторите те же измерения и вычисления для трубки 3 с раствором неизвестной концентрации С 3; все данные занесите в табл. 4.3.
Таблица 4.3
Задание 3. Определение толщины кварцевой пластинки 1. Поворотом винта 4 добейтесь максимального затемнения крайних полей зрения. При этом шторка прибора должна быть закрыта; в приборе не должно быть трубки с раствором. 2. Запишите в табл.4.4 отсчёт n 1 по шкале. 3. Добейтесь максимального затемнения среднего поля зрения; запишите отсчёт n 2. 4. Повторите измерения n 1 и n 2 не менее пяти раз. 5. Вычислите средние значения n 1ср. и n 2ср.; рассчитайте их разность: φ=(n 1ср.– n 2ср) – это и будет угол поворота плоскости поляризации света кварцевой пластинкой, сквозь которую проходит центральная часть пучка. 6. По формуле (4.3) рассчитайте толщину пластинки. 7. Оцените погрешность Δ l; все результаты запишите в табл.4.4. 8. Сделайте выводы.
Таблица 4.4
Контрольные вопросы 1. Что такое естественный и поляризованный свет? 2. Укажите способы получения поляризованного света. 3. В чем заключается явление двойного лучепреломления? 4. Изобразите ход лучей в призме Николя. 5. Сформулируйте и докажите закон Малюса. 6. Какие вещества называются оптически активными? 7. Что такое удельное вращение? От чего оно зависит? 8. Объясните механизм вращения плоскости поляризации по теории Френеля. 9. Почему кварц в твёрдом состоянии оптически активен, а в жидком – нет? 10. Объясните назначение основных элементов поляриметра и принцип его действия. Используемая литература [1] §§ 34.1, 34.5; [2] § 26.1; [3] §§ 3.31, 3.47; [5] §§ 98, 100, 101; [7] §§ 190, 192, 193, 196. Лабораторная работа 3-05 Изучение зависимости показателя преломления стеклянной призмы от длины волны Цель работы: изучение явления дисперсии белого света и построение дисперсионной кривой. Теоретическое введение Дисперсией света называется зависимость показателя преломления n вещества от частоты n (длины волны l) света или фазовой скорости v световых волн от его частоты n.
Дисперсия света представляется в виде зависимости:  ; ;  . Первое экспериментальное исследование дисперсии света было выполнении Ньютоном в 1672 г. Следствием дисперсии является разложение в спектр белого света при прохождении его через призму (рис.5.1). После прохождения света через призму образуется спектр, в котором линии каждой частоты (длины волны) занимают совершенно определенное место. Величина . Первое экспериментальное исследование дисперсии света было выполнении Ньютоном в 1672 г. Следствием дисперсии является разложение в спектр белого света при прохождении его через призму (рис.5.1). После прохождения света через призму образуется спектр, в котором линии каждой частоты (длины волны) занимают совершенно определенное место. Величина
называемая дисперсией вещества, показывает, как быстро изменяется показатель преломления с длиной волны. Различают два вида дисперсии: нормальную (D <0),
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.233.32 (0.017 с.) |

 Двойное лучепреломление может возникать в прозрачных изотропных телах, а также в кристаллах кубической системы под влиянием различных воздействий: сильного однородного электрического (эффект Керра) или магнитного поля, а также при механических деформациях тел. Мерой возникающей оптической анизотропии может служить разность показателей преломления обыкновенного и необыкновенного лучей. Опыт показывает, что эта разность пропорциональна механическому напряжению σ в данной точке тела (то есть силе, приходящейся на единицу площади):
Двойное лучепреломление может возникать в прозрачных изотропных телах, а также в кристаллах кубической системы под влиянием различных воздействий: сильного однородного электрического (эффект Керра) или магнитного поля, а также при механических деформациях тел. Мерой возникающей оптической анизотропии может служить разность показателей преломления обыкновенного и необыкновенного лучей. Опыт показывает, что эта разность пропорциональна механическому напряжению σ в данной точке тела (то есть силе, приходящейся на единицу площади): , (3.7)
, (3.7)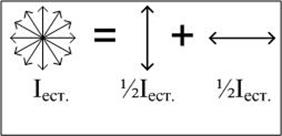 Пусть на неидеальный поляроид падает естественный свет интенсивностью Iест. Представим его в виде суперпозиции двух некогерентных линейно поляризованных во взаимно перпендикулярных плоскостях лучей одинаковой интенсивности
Пусть на неидеальный поляроид падает естественный свет интенсивностью Iест. Представим его в виде суперпозиции двух некогерентных линейно поляризованных во взаимно перпендикулярных плоскостях лучей одинаковой интенсивности  (рис.3.9). Предположим, что через неидеальный поляроид без поглощения проходит луч, поляризованный в направлении оптической оси, (
(рис.3.9). Предположим, что через неидеальный поляроид без поглощения проходит луч, поляризованный в направлении оптической оси, ( ), а луч, поляризованный перпендикулярно оптической оси, частично поглощается, так что
), а луч, поляризованный перпендикулярно оптической оси, частично поглощается, так что  . Пусть
. Пусть . (3.8)
. (3.8) Величина K характеризует качество неидеального поляроида. Для идеального
Величина K характеризует качество неидеального поляроида. Для идеального  . Если в качестве анализатора использовать идеальный поляроид, то обе величины,
. Если в качестве анализатора использовать идеальный поляроид, то обе величины,  и
и  , можно измерить, пропустив частично поляризованный свет, вышедший из неидеального поляроида, через идеальный поляроид и измерив интенсивности Imax и Imin; это будут I॥ и I^ соответственно. Тогда
, можно измерить, пропустив частично поляризованный свет, вышедший из неидеального поляроида, через идеальный поляроид и измерив интенсивности Imax и Imin; это будут I॥ и I^ соответственно. Тогда . (3.9)
. (3.9) : (3.10)
: (3.10) , (3.11)
, (3.11) . (3.12)
. (3.12) , (3.13)
, (3.13) раз:
раз: . (3.14)
. (3.14) . (3.15)
. (3.15) , (3.16)
, (3.16) раз:
раз: . (3.17)
. (3.17) . (3.18)
. (3.18) . (3.19)
. (3.19)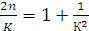 ;
; ;
; . (3.20)
. (3.20) . (3.21)
. (3.21)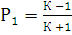 , (3.22)
, (3.22) . (3.23)
. (3.23) . (3.24)
. (3.24) (поляроиды скрещены) из (3.26) получим:
(поляроиды скрещены) из (3.26) получим:  , а при
, а при  (поляроиды параллельны)
(поляроиды параллельны)  .
. При нормальном падении пучка лучей на пластинку из кристалла, оптическая ось y которого параллельна преломляющей поверхности, обыкновенный и необыкновенный лучи идут по одному направлению, но с разными скоростями. Пусть на такую пластинку падает плоско поляризованный луч с амплитудой электрического вектора E 0, плоскость поляризации которого составляет с плоскостью главного сечения пластинки ОО´ угол φ. Тогда в пластинке возникнут оба луча, обыкновенный (о) и необыкновенный (е) (рис. 3.10), и они будут когерентны. В момент их возникновения в пластинке разность фаз между ними равна нулю, но она будет возрастать по мере проникновения лучей в пластинку. Подсчитаем эту разность фаз.
При нормальном падении пучка лучей на пластинку из кристалла, оптическая ось y которого параллельна преломляющей поверхности, обыкновенный и необыкновенный лучи идут по одному направлению, но с разными скоростями. Пусть на такую пластинку падает плоско поляризованный луч с амплитудой электрического вектора E 0, плоскость поляризации которого составляет с плоскостью главного сечения пластинки ОО´ угол φ. Тогда в пластинке возникнут оба луча, обыкновенный (о) и необыкновенный (е) (рис. 3.10), и они будут когерентны. В момент их возникновения в пластинке разность фаз между ними равна нулю, но она будет возрастать по мере проникновения лучей в пластинку. Подсчитаем эту разность фаз. . (3.25)
. (3.25) , (3.26)
, (3.26)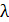 – длина волны в вакууме.
– длина волны в вакууме.

 Отличие установки № 2 (рис.3.13) от № 1 состоит в том, что здесь использованы более качественные поляроиды (1 и 2), а приёмником излучения служит фотоэлемент 3 с блоком индикации 4. Накал лампы можно изменять регулятором 5.
Отличие установки № 2 (рис.3.13) от № 1 состоит в том, что здесь использованы более качественные поляроиды (1 и 2), а приёмником излучения служит фотоэлемент 3 с блоком индикации 4. Накал лампы можно изменять регулятором 5. . (3.19)
. (3.19) , мкА
, мкА
 , мкА
, мкА


 . (3.24)
. (3.24) в каждом случае по формуле (3.25), рассчитайте среднее значение.
в каждом случае по формуле (3.25), рассчитайте среднее значение. . (3.25)
. (3.25)

 каким-либо образом упорядочить, то свет будет поляризованным. Если колебания вектора
каким-либо образом упорядочить, то свет будет поляризованным. Если колебания вектора  ,
,  . (4.1)
. (4.1) Первая составляющая колебаний пройдет через анализатор, вторая будет задержана им. Интенсивность света пропорциональна квадрату амплитуды, следовательно, интенсивность света, прошедшего через анализатор, пропорциональна
Первая составляющая колебаний пройдет через анализатор, вторая будет задержана им. Интенсивность света пропорциональна квадрату амплитуды, следовательно, интенсивность света, прошедшего через анализатор, пропорциональна  (закон Малюса):
(закон Малюса): , (4.2)
, (4.2) – интенсивность поляризованного света, падающего на анализатор; φ – угол между плоскостью колебаний падающего света и главной плоскостью анализатора.
– интенсивность поляризованного света, падающего на анализатор; φ – угол между плоскостью колебаний падающего света и главной плоскостью анализатора. , поэтому при пропускании поляризованного света через раствор оптически активного вещества плоскости поляризации волн различной длины будут поворачиваться на разные углы. В зависимости от положения анализатора через него проходят лучи различной окраски. Это явление называется вращательной дисперсией.
, поэтому при пропускании поляризованного света через раствор оптически активного вещества плоскости поляризации волн различной длины будут поворачиваться на разные углы. В зависимости от положения анализатора через него проходят лучи различной окраски. Это явление называется вращательной дисперсией. и
и 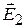 вращаются с одинаковой скоростью, то геометрическая сумма их в каждый момент времени будет лежать в одной и той же плоскости Р (рис. 4.2, а).
вращаются с одинаковой скоростью, то геометрическая сумма их в каждый момент времени будет лежать в одной и той же плоскости Р (рис. 4.2, а). Если скорости распространения обеих волн окажутся неодинаковыми, то по мере прохождения через вещество один из векторов,
Если скорости распространения обеих волн окажутся неодинаковыми, то по мере прохождения через вещество один из векторов,  Различие в скоростях света с разным направлением круговой поляризации обусловливается асимметрией молекул, либо асимметричным размещением атомов в кристалле. На рис. 4.3 приведен пример асимметричной молекулы. В центре тетраэдра помещается атом углерода, в вершинах – отличающиеся друг от друга атомы или группировки атомов (радикалы), обозначенные буквами X, Y, Z и V. Молекула, изображенная на рис.4.3,б, является зеркальным отражением молекулы, показанной на рис. 4.3,а. У них нет ни центра симметрии, ни плоскости симметрии, и они не могут быть пространственно совмещены друг с другом никакими поворотами и перемещениями. Физические и химические свойства чистых оптических изомеров совершенно одинаковы. Но если, например, вещество, образованное молекулами а, правовращающее, то вещество, образованное молекулами б, будет левовращающим. Значения удельного вращения для обеих модификаций отличаются только знаком.
Различие в скоростях света с разным направлением круговой поляризации обусловливается асимметрией молекул, либо асимметричным размещением атомов в кристалле. На рис. 4.3 приведен пример асимметричной молекулы. В центре тетраэдра помещается атом углерода, в вершинах – отличающиеся друг от друга атомы или группировки атомов (радикалы), обозначенные буквами X, Y, Z и V. Молекула, изображенная на рис.4.3,б, является зеркальным отражением молекулы, показанной на рис. 4.3,а. У них нет ни центра симметрии, ни плоскости симметрии, и они не могут быть пространственно совмещены друг с другом никакими поворотами и перемещениями. Физические и химические свойства чистых оптических изомеров совершенно одинаковы. Но если, например, вещество, образованное молекулами а, правовращающее, то вещество, образованное молекулами б, будет левовращающим. Значения удельного вращения для обеих модификаций отличаются только знаком. Используемый в работе прибор изображен на рис. 4.4. Его основные части: два николя I и II, расположенные в металлической трубке 1, поддерживаемой штативом 2. На николь I падает естественный луч света от источника 3. Поляризованный луч света падает на николь II, который может поворачиваться при помощи кремальеры (винта) 4 вокруг оси прибора. Углы поворота николя II отсчитываются при помощи нониуса по разделенному градусному лимбу в окуляре 7.
Используемый в работе прибор изображен на рис. 4.4. Его основные части: два николя I и II, расположенные в металлической трубке 1, поддерживаемой штативом 2. На николь I падает естественный луч света от источника 3. Поляризованный луч света падает на николь II, который может поворачиваться при помощи кремальеры (винта) 4 вокруг оси прибора. Углы поворота николя II отсчитываются при помощи нониуса по разделенному градусному лимбу в окуляре 7. В работе используется медицинский сахариметр, оптическая схема которого приведена на рисунке 4.5.
В работе используется медицинский сахариметр, оптическая схема которого приведена на рисунке 4.5. Поворачивая анализатор, можно получить равномерно освещенное поле зрения. Это происходит при двух положениях анализатора: 1) плоскость АА анализатора совпадает с биссектрисой угла между направлениями колебаний в средней и крайних частях поля зрения (рис. 4.6, б); 2) плоскость анализатора перпендикулярна биссектрисе угла между направлениями колебаний (рис. 4.6, в).
Поворачивая анализатор, можно получить равномерно освещенное поле зрения. Это происходит при двух положениях анализатора: 1) плоскость АА анализатора совпадает с биссектрисой угла между направлениями колебаний в средней и крайних частях поля зрения (рис. 4.6, б); 2) плоскость анализатора перпендикулярна биссектрисе угла между направлениями колебаний (рис. 4.6, в). Если установить анализатор на равную освещенность всех частей поля зрения, а затем поместить между поляризатором и анализатором трубку с раствором сахара, то равенство яркостей средней и крайней частей поля зрения нарушится. Это происходит в результате того, что во всех частях поля зрения плоскость колебаний светового вектора повернется на один и тот же угол a (рис. 4.7). Для восстановления равенства освещенностей необходимо повернуть анализатор на этот же угол a, равный углу поворота плоскости поляризации света при прохождении им раствора сахара.
Если установить анализатор на равную освещенность всех частей поля зрения, а затем поместить между поляризатором и анализатором трубку с раствором сахара, то равенство яркостей средней и крайней частей поля зрения нарушится. Это происходит в результате того, что во всех частях поля зрения плоскость колебаний светового вектора повернется на один и тот же угол a (рис. 4.7). Для восстановления равенства освещенностей необходимо повернуть анализатор на этот же угол a, равный углу поворота плоскости поляризации света при прохождении им раствора сахара. ,
град
,
град

 плоскости поляризации для этого раствора.
плоскости поляризации для этого раствора.
 , (5.1)
, (5.1)


