
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика измерений и описание установкиСодержание книги
Поиск на нашем сайте
В предлагаемом методе определения динамического коэффициента вязкости используется истечение воздуха через капилляр. Известно, что скорости истечения бесконечно тонких цилиндрических слоев воздуха, расположенных на различных расстояниях от оси капилляра, различны и распределены по сечению капилляра по параболическому закону. Наибольшая скорость будет на осевой линии капилляра и, по мере приближения к стенкам, скорость уменьшается, а слой, прилегающий к стенке, неподвижен, т.е. "прилипает" к ней. Между слоями, движущимися с различными скоростями, возникает сила внутреннего трения (сила вязкости). При установившемся движении сила вязкости, действующая на элементарный объем и приложенная к боковой поверхности цилиндра, уравновешивает разность сил давлений, действующих на основание цилиндра. На концах капилляра при протекании по нему воздуха возникает разность давлений (p 1– p 2). При установившемся движении воздуха она будет неизменной. По закону Пуазейля, при малых скоростях течения объем воздуха, протекающего через сечение капилляра, равен:
где r – радиус капилляра; (p 1– p 2) – разность давлений в начале и конце капилляра; h - динамический коэффициент вязкости; l – длина капилляра; V – объем газа, протекшего через сечение капилляра за время t. Отсюда
Таким образом, для определения коэффициента вязкости достаточно измерить разность давлений, время истечения газа, его объем, радиус и длину капилляра.
Давление p 2 уравновешивается атмосферным: p 2= p атм., тогда
Учитывая, что давление у верхнего конца капилляра равно атмосферному, разность давлений на концах капилляра выразится из (12.15):
Поскольку в процессе опыта давление столба воды уменьшается (за счет истечения), то берут среднее значение
и выражение для вязкости (12.13) примет вид:
Порядок выполнения работы 1. Подготовьте установку к выполнению работы: а) залейте сосуд на 3/4 объема водой; б) закройте сверху плотно трубкой с капилляром; в) подставьте под кран сливную емкость; г) подготовьте к работе секундомер. 2. Откройте кран К. Когда вода начнет вытекать каплями: а) отметьте уровень воды h 1; б) подставьте мерный сосуд под трубку D; г) запустите секундомер. 3. Когда в мерном сосуде будет 50 мл воды: а) отметьте по шкале новый уровень воды h 2. При этом объем воды в мерном сосуде равен объему прошедшего через капилляр воздуха; б) одновременно с этим остановите секундомер. 4. Результаты измерений занесите в таблицу 12.1. 5. Опыт повторите 3-5 раз, фиксируя каждый раз h 1, h 2 и время истечения воздуха t. 6. Полученные результаты каждого опыта подставьте в (12.19) и рассчитайте коэффициент вязкости h, рассчитайте среднее значение коэффициента вязкости. Длина капилляра равна l =4 см, его радиус r =0.06 мм. 7. Рассчитайте абсолютную D h и относительную 8. Полученный результат для коэффициента вязкости h подставьте в (12.13) и рассчитайте l. 9. Выведите формулу и рассчитайте погрешность Dl, а также 10. Результаты вычислений занесите в таблицу 12.1.
Таблица 12.1
Контрольные вопросы 1. Объясните молекулярно-кинетический механизм вязкости. 2. Сформулируйте и докажите закон Ньютона для вязкости; получите выражение для коэффициента вязкости. 3. Каков физический смысл коэффициента динамической вязкости? 4. От каких параметров и как зависит коэффициент вязкости воздуха? 5. Сформулируйте закон Пуазейля. Как он используется в данной лабораторной работе? Выведите рабочую формулу (12.19) для коэффициента вязкости. 6. Что такое средняя длина свободного пробега? От чего она зависит? Выведите расчётную формулу (12.13). 7. Какие ещё явления переноса, кроме вязкости, вы знаете? Что при этом переносится? Используемая литература [1] §§ 10.6-10.8; [2] §§ 36.1-36.3; [3] §§ 5.6, 5.7; [4] §§ 78-80; [7] §§ 46, 48.
Лабораторная работа 3-13
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.68.161 (0.007 с.) |

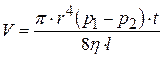 , (12.14)
, (12.14) . (12.15)
. (12.15) Схема установки представлена на рис.12.3. Установка состоит из стеклянного сосуда А со шкалой C. Верхняя часть сосуда закрыта пробкой с капилляром B, а в нижней имеется трубка с краном К. Перед началом работы кран закрыт, сосуд заполнен водой на 3/4 объема и плотно закрыт пробкой с капилляром. Если открыть кран К, то по истечении некоторого времени вода из сосуда А будет вытекать каплями. При этом объем воды, вытекающий из сосуда, равен объему воздуха, прошедшего через капилляр, а давление p 2 у открытого конца трубки D равно сумме давлений: давления p 1 воздуха, находящегося над поверхностью воды в сосуде А, и гидростатического давления
Схема установки представлена на рис.12.3. Установка состоит из стеклянного сосуда А со шкалой C. Верхняя часть сосуда закрыта пробкой с капилляром B, а в нижней имеется трубка с краном К. Перед началом работы кран закрыт, сосуд заполнен водой на 3/4 объема и плотно закрыт пробкой с капилляром. Если открыть кран К, то по истечении некоторого времени вода из сосуда А будет вытекать каплями. При этом объем воды, вытекающий из сосуда, равен объему воздуха, прошедшего через капилляр, а давление p 2 у открытого конца трубки D равно сумме давлений: давления p 1 воздуха, находящегося над поверхностью воды в сосуде А, и гидростатического давления  :
: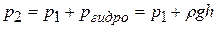 . (12.16)
. (12.16) . (12.17)
. (12.17)
 , (12.18)
, (12.18)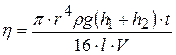 . (12.19)
. (12.19) погрешности.
погрешности. .
.


