
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение постоянной Стефана-БольцманаСодержание книги
Поиск на нашем сайте
Цель работы: ознакомление с законами теплового излучения, измерение постоянной Стефана-Больцмана. Теоретическое введение Поток световой энергии, падающий на поверхность непрозрачного тела, частично входит внутрь тела и поглощается. Поглощенная телом энергия преобразуется в другие формы энергии, чаще всего в энергию теплового движения. Поэтому тела, поглощающие лучи, нагреваются. Тело, нагретое до температуры большей, чем температура окружающей среды, отдает в виде излучения электромагнитных волн различных длин теплоту (непрерывный спектр). Всякое излучение сопровождается потерей энергии и происходит либо за счет внутренней энергии, либо за счет получения энергии извне. Излучение тела, обусловленное тепловым движением молекул, называется тепловым, так как происходит за счёт энергии теплового движения молекул. Любое тело с температурой Т≠0, излучает, причём спектр излучения – сплошной. Если уменьшение энергии тела при излучении восполняется за счёт поглощения излучения, падающего на тело, то излучение называется равновесным. Тепловое излучение тел может быть охарактеризовано двумя основными величинами: 1. Интегральная интенсивность излучения, численно равна энергии всех длин волн, излучаемой в единицу времени с единичной площади поверхности тела:
Эту величину называют также полной энергетической светимостью. Она зависит от абсолютной температуры тела. 2. Монохроматическая (дифференциальная) интенсивность излучения (спектральная плотность энергетической светимости) численно равна энергии, излучаемой в единицу времени с единичной площади поверхности тела в единичном интервале длин волн:
или частот:
Монохроматическая интенсивность излучения является функцией длины волны и температуры (6.2) или частоты и температуры (6.2а). Из определения вытекает связь между интегральной и монохроматической интенсивностями излучения:
Из всей падающей на тело энергии dWпадающ. монохроматического света в интервале длин волн [l; l+dl] часть энергии dWпоглощ. поглощается телом. 3. Величина
Наиболее совершенной моделью черного тела может служить небольшое отверстие в непрозрачной стенке замкнутой полости (рис.6.1). Луч света, попадающий внутрь через отверстие, претерпевает многократные отражения от стенок полости, прежде чем он выйдет обратно. При каждом отражении происходит частичное поглощение энергии света стенками. Поэтому независимо от материала стенок интенсивность света, выходящего из полости через отверстие, во много раз меньше интенсивности падающего извне первичного излучения. Эта модель тем ближе по характеристикам к чёрному телу, чем больше отношение площади поверхности полости к площади отверстия. Законы теплового излучения Закон Кирхгофа. Исходя из второго начала термодинамики, Кирхгоф показал, что условие теплового равновесия заключается в следующем: отношение монохроматической интенсивности излучения к поглощательной способности тела не зависит от природы тела; является универсальной (одинаковой для всех тел) функцией длины волны и температуры (универсальная функция Кирхгофа):
Следовательно, тело, поглощающее какие-либо лучи, будет их же и излучать, и наоборот. Величина e(l,Т) не зависит от природы тела и является функцией лишь длины волны и температуры. Так как для абсолютно черного тела al,Т =1, то
Для многих тел поглощательную способность можно считать не зависящей от длины волны: al,Т = а =const<1. Такие тела называются серыми, величина а называется коэффициентом серости. Эксперименты показали, что зависимость e(l) при различных температурах черного тела имеет вид, изображенный на рис.6.2. По мере повышения температуры максимум смещается в область коротких волн, а интенсивность излучения растет. Эти закономерности излучения АЧТ описываются законами Вина. Первый закон Вина (закон смещения Вина). Длина волны lm, на которую приходится максимум монохроматической интенсивности излучения, обратно пропорциональна температуре:
Второй закон Вина. Максимальное значение спектральной плотности энергетической светимости прямо пропорционально пятой степени абсолютной температуры:
Первая и вторая константы Вина в (6.6.) и (6.7) равны соответственно: b =2.9.10-3 м.К, В соответствии с (6.3) площадь под графиком функции e(l) равна полной энергетической светимости АЧТ. По закону Стефана-Больцмана полная энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры: RT = sT 4. (6.8) Постоянная Стефана-Больцмана s была определена опытным путем: s=5.67.10-8 Вт/(м2.К4). Излучение серых тел подчиняется аналогичной закономерности, однако излучение их для каждой длины волны меньше, чем для абсолютно черного тела. Полное излучение RT = аsT 4. (6.8а)
Полученная ими формула
хорошо согласовывалась с данными опыта только в области малых частот излучения. На рис.6.3 пунктир 1 соответствует формуле Рэлея-Джинса; сплошная кривая 2 – экспериментальная зависимость. Для больших частот (6.10) даёт Классическая физика оказалась несостоятельной при описании теплового излучения. Невозможность решения проблемы теплового излучения методами классической физики назвали «ультрафиолетовой катастрофой». Гипотеза и формула Планка. Причина «ультрафиолетовой катастрофы» оказалась лежащей чрезвычайно глубоко. Законы классической электродинамики давали неверный результат при рассмотрении элементарных процессов, обуславливающих тепловое излучение. Выход из создавшегося положения указал Макс Планк, выдвинув гипотезу, совершенно чуждую представлениям классической физики. Он предположил, что электромагнитное излучение испускается и поглощается дискретными порциями энергии – квантами электромагнитного поля (фотонами). Энергия такого кванта пропорциональна частоте колебания
а коэффициент пропорциональности h =6.63.10-34Дж.с – постоянная Планка – получил название в честь автора квантовой гипотезы. Так как излучение испускается порциями, то энергия квантового осциллятора ε может принимать лишь определённые дискретные значения, кратные целому числу элементарных порций энергии ε0: ε= nhν (n =0, 1, 2…). Распределение квантовых осцилляторов по возможным дискретным состояниям подчиняется закону Больцмана; тогда средняя энергия осциллятора
где k= 1.38.10-23Дж/с – постоянная Больцмана. Исходя из того, что в состоянии термодинамического равновесия расход энергии на излучение осцилляторов с собственной частотой ν должен полностью компенсироваться в результате поглощения этими осцилляторами энергии падающего на них излучения, Планк показал, что
Тогда спектральная плотность энергетической светимости АЧТ
или, при переходе от частоты к длине волны:
Это и есть формула Планка. Если бы для определения средней энергии Формула Планка правильно описывает экспериментальную кривую рис.6.2, на её основе были объяснены все экспериментально открытые законы теплового излучения, не находившие своего объяснения в рамках классической физики. Так, например, из (6.14а) и (6.3) можно получить закон Стефана-Больцмана (6.8) интегрированием функции Планка по всему интервалу длин волн:
где
Из формулы Планка можно получить также законы Вина, решив уравнение Тепловое излучение – единственное излучение, способное находиться в термодинамическом равновесии с веществом. При динамическом равновесии энергия, расходуемая телом на тепловое излучение, компенсируется вследствие поглощения этим телом такого же количества энергии падающего на него излучения. Отсюда следует, что если абсолютно чёрное тело находится в среде, имеющей температуру Т2, и среду можно рассматривать как абсолютно чёрное тело, то поток поглощённой телом энергии определяется из закона Стефана-Больцмана:
Или, с учетом коэффициента серости,
Излучение накаливаемой током нити, покрытой окалиной, близко к излучению абсолютно черного тела. Приравнивая мощность, затрачиваемую на поддержание нити в накаленном состоянии P=IU, и мощность, излучаемую с ее поверхности, получаем выражение
где I и U соответственно сила тока и напряжение, а S – полная площадь поверхности нити. Используя (6.19), можно опытным путем определить постоянную Стефана - Больцмана:
Экспериментальная часть Приборы и оборудование: оптический пирометр ЛОП-72, блок, содержащий миллиамперметр, реостат, источники постоянного тока, источник света. Описание установки Используемая в работе установка (рис.6.4) состоит из пирометра 1, лампы накаливания 2, амперметра 3, вольтметра 4, реостата 5, источника постоянного напряжения 12 В. Основной частью установки является пирометр с исчезающей нитью, при помощи которого определяется температура нити накаливания.
Так как обычные тела излучают не так, как черное тело, то данная температура не будет истинной. Ее называют яркостной температурой тела. Действительная температура находится либо при помощи таблиц, прилагаемых к описанию пирометра, либо по графику. Данный пирометр позволяет измерить температуру нагретого тела в интервале 700оС и выше. Введение дымчатого светофильтра позволяет увеличить температуру до 2000оС. Порядок выполнения работы 1. Включить установку в сеть. Включить тумблер «сеть» на блоке питания. 2. Убедиться, что лампа пирометра горит и накал ее можно менять реостатом 8. Добиться, чтобы в поле зрения пирометра на фоне верхушки нити пирометра была видна нить исследуемой лампы.
4. Полученные значения яркостной температуры, силы тока и напряжения занести в таблицу 6.1. 5. Повторить измерения при других значениях силы тока через лампу (всего 5-6 измерений), добиваясь каждый раз исчезновения нити пирометра на фоне исследуемой лампы. 6. По данным таблицы 6.2 построить график зависимости Тдейст.= f (Тярк). 7. Зная яркостную температуру нити исследуемой лампы, найти по градуировочному графику ее действительную температуру; все данные занести в табл.6.1. 8. По формуле (6.20) вычислить постоянную Стефана-Больцмана в каждом опыте. Принять а =0.43; S =25 мм2. 9. Найти среднее значение σсреднее и рассчитать погрешность Δσ. Все результаты занести в табл.6.1. 10. Из формулы (6.16) выразить постоянную Планка, и, воспользовавшись значением σсреднее, вычислить экспериментальное значение h. Сравнить с табличным. Сделать выводы.
Таблица 6.1
Таблица 6.2
Контрольные вопросы 1. Дайте определение спектральной плотности энергетической светимости, полной излучательной способности, поглощательной способности. Каковы размерности этих величин? 2. Какое излучение называется тепловым? 3. Что такое абсолютно чёрное тело? 4. Сформулируйте законы теплового излучения. 5. Напишите формулу Рэлея-Джинса. Что такое «ультрафиолетовая катастрофа»? 6. Сформулируйте гипотезу Планка о квантовании энергии излучения. Запишите формулу Планка. 7. Как из формулы Планка получить законы Стефана-Больцмана и Вина? 8. Почему яркостная температура, измеряемая пирометром, не совпадает с действительной? Объясните устройство и принцип действия пирометра. Используемая литература [1] §§ 35.1-35.3; [2] §§ 27.1-27.4; [3] §§ 4.8-4.10; [6] §§ 1-6; [7] §§ 197-201. Лабораторная работа 3-07 Изучение явления внешнего фотоэффекта Цель работы: определение характеристик фотоэлемента. Теоретическое введение Одним из явлений, подтверждающих гипотезу фотонов, является фотоэлектрический эффект. Явление вырывания электронов с поверхности твёрдых и жидких тел под действием света (электромагнитного излучения) называется внешним фотоэффектом. Впервые явление фотоэффекта было открыто Г.Герцем в 1887г.: он заметил, что при освещении ультрафиолетовыми лучами металлическое тело теряет электроны. Первые количественные исследования фотоэффекта сделал А.Г.Столетов, который установил основные законы фотоэффекта. Позже установка Столетова была усовершенствована Ф.Э.А.Ленардом (рис. 7.1).
Свет, проникающий через кварцевое окно Кв (кварц пропускает ультрафиолетовые лучи), освещает катод К, изготовленный из исследуемого материала. Электроны, испущенные вследствие фотоэффекта, перемещаются под действием электрического поля к аноду А. В цепи возникает фототек, измеряемый гальванометром Г. С помощью потенциометра П можно изменять напряжение между катодом и анодом, которое показывает вольтметр В. Законы фотоэффекта. Проанализируем вольт-амперную характеристику (т.е. зависимость фототока I от напряжения между электродами U), которая получается в результате фотоэлектрического эффекта. Из кривой на рис. 7.2 видно, что при некотором не очень большом напряжении фототок достигает насыщения – все электроны, испущенные катодом, попадают на анод. Следовательно, сила тока насыщения I н определяется количеством электронов, испускаемых катодом в единицу времени под действием света. Поэтому сила тока насыщения Iн прямо пропорциональна световому потоку I н = γ Ф, (7.1) где γ – коэффициент пропорциональности, характеризующий чувствительность данной поверхности к свету. Анализ кривой показывает, что электроны вылетают из катода с различными по величине скоростями. Часть электронов обладает достаточными скоростями, чтобы при U =0 долететь до анода «самостоятельно» и создать ток I ≠0 без помощи ускоряющего поля. Для обращения фототока в нуль необходимо приложить некоторое задерживающее напряжение U з. По величине тормозящей разности потенциалов U 3, при которой фототок обращается в нуль, можно определить скорость самых быстрых фотоэлектронов:
Экспериментально было установлено, что максимальная скорость фотоэлектронов не зависит от интенсивности света, а зависит только от частоты излучения, и эта зависимость – линейная. Эта экспериментальная зависимость не укладывается в рамки классической электродинамики, так как скорость фотоэлектронов по классическим понятиям должна зависеть от интенсивности электромагнитной волны, а не от ее частоты. Классическая электродинамика не смогла объяснить и безынерционность фотоэффекта, а также ещё один закон фотоэффекта – существование красной границы: для каждого материала имеется своя граничная частота ν0, при которой начинается фотоэффект, так что при частоте света ν≥ν0 фотоэффект наблюдается, а при ν< ν0 – нет. Уравнение Эйнштейна. В 1905 г. А. Эйнштейн показал, что все закономерности фотоэффекта легко объясняются, если предположить, что свет распространяется и поглощается такими же порциями (квантами) Энергия, полученная электроном, доставляется ему в виде кванта hν. Часть этой энергии электрон тратит на то, чтобы вырваться из металла. Для каждого материала имеется своя работа выхода Авых –наименьшая энергия, которую необходимо сообщить электрону, чтобы удалить его из вещества в вакуум. Остаток энергии фотона (hν –Авых) тратится на кинетическую энергию (m v2/2) электрона. Кинетическая энергия максимальна, если электрон образуется вблизи поверхности вещества и не расходует энергию на случайные столкновения в веществе. В этом случае будет выполняться уравнение Эйнштейна:
Уравнение Эйнштейна позволяет объяснить законы фотоэффекта. Действительно, из соотношения Эйнштейна непосредственно следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности. Так как с уменьшением частоты падающего света кинетическая энергия фотоэлектронов уменьшается (для данного вещества катода Авых постоянна), то при достижении некоторой критической частоты ν=ν0 кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится. Согласно Эйнштейну, частота
Эта частота
называется красной границей фотоэффекта. Она зависит лишь от работы выхода электронов, то есть от химической природы вещества и состояния его поверхности.
Экспериментальная часть Старая установка Приборы и оборудование:фотоэлемент, осветитель, выпрямитель, гальванометр, измерительная линейка.
Методика измерений На явлении фотоэффекта основано действие фотоэлементов – приборов, находящих широкое применение в науке, технике, народном хозяйстве. Каждый фотоэлемент характеризуется рядом параметров, определяющих не только его свойства, но и пределы применимости. Важнейшими параметрами фотоэлементов являются: интегральная и спектральная чувствительности, вольт-амперная характеристика, рабочее напряжение и др. Под интегральной чувствительностью g понимают величину фототока, который течет в короткозамкнутой цепи фотоэлемента при падении на него единичного потока лучистой энергии, состоящей из волн различной длины. Таким образом,
где I – ток в цепи фотоэлемента, Ф – падающий на фотоэлемент световой поток. Когда приходится иметь дело с видимой областью спектра, величину светового потока выражают в люменах, и в этом случае [g]=А/лм. Освещённость Е поверхности фотоэлемента площадью S равна
Освещённость, создаваемая точечным изотропным источником света на расстоянии r от него при нормальном падении света:
где I св. – сила света точечного источника. Тогда чувствительность
Другой важной характеристикой фотоэлемента является световая характеристика. Она показывает, как изменяется фототок I при изменении освещенности фотоэлемента Е. График зависимости I = f (Е) позволяет судить об области применимости того или иного фотоприемника. Световая характеристика фотоэлемента, действие которого основано на внешнем фотоэффекте, позволяет убедиться в одном из законов фотоэффекта: количество вылетающих электронов пропорционально количеству падающих на вещество фотонов; каждый фотон взаимодействует с одним электроном. Вольтамперные характеристики отражают зависимость фототока от приложенного к фотоэлементу напряжения при неизменном световом потоке. Эта характеристика позволяет правильно выбрать рабочее напряжение фотоэлемента. Семейство кривых I=f (U), снятых при различных уровнях освещенности, хорошо иллюстрируют теорию фотоэффекта Эйнштейна. Экспериментальная установка
Схема экспериментальной установки приведена на рис.7.3. В работе используется вакуумный фотоэлемент СЦВ-3 (1). Для защиты от постороннего света он смонтирован в кожухе. Фотоэлемент представляет собой стеклянный баллон, из которого до определенного давления откачан воздух. На половину внутренней поверхности баллона напылением наносится слой металла (в СЦВ-3 – цезий), являющийся фотокатодом. Анод имеет форму металлической сферы и расположен в центральной части баллона. Электрические части катода и анода впаяны в нижнюю часть баллона и вмонтированы в цоколь фотоэлемента. Фотоэлемент и осветитель (2) расположены на рельсах так, что расстояние между ними можно менять. При освещении фотокатода в цепи фотоэлемента возникает ток, измеряемый гальванометром (3). Напряжение подается от выпрямителя (4), смонтированного с вольтметром (5) в одном корпусе. Выпрямитель включается в сеть переменного тока проводом (6) и тумблером SA1. Величину напряжения можно изменять потенциометром R и измерять вольтметром. С помощью данной установки можно снять вольтамперную характеристику фотоэлемента (зависимость силы фототока от напряжения при постоянном расстоянии между осветителем и фотоэлементом: I=f (U)) и световую характеристику (зависимость фототока насыщения от освещенности: I = f (Е)). Перед началом измерений следует установить пределы измерений амперметра и вольтметра и определить цену их делений. Порядок выполнения работы Задание 1. Снять вольтамперную характеристику фотоэлемента. 1. Ознакомиться с установкой. 2. Установить предел измерений вольтметра 30 В (тумблер U ф установить в положение 0-30). 3. Поставить фотоэлемент на расстоянии12 см от осветителя и, изменяя напряжение от минимального до максимального (см. табл.7.1), записывать значения соответствующего тока. Для того, чтобы установить напряжение U> 30 В, тумблер U ф установить в положение 0-300. При этом предел измерений вольтметра равен 300 В. 4. Повторить измерения при других значениях расстояния r; все результаты записать в табл.7.1. 5. Построить графики I = f (U) для расстояний r =12, 14 и 18 см (в одних и тех же осях).
Задание 2. Получение световой характеристики фотоэлемента. 1. По таблице 7.1 определить для каждого r силу тока насыщения I нас, записать в табл.7.2. 2. Рассчитать освещённость Е по формуле (7.8). Силу света лампочки принять I cв.= 116 кд (единица силы света – кандела, она равна 3. Построить график зависимости I нас.= f (E). Таблица 7.1
Задание 3. Определение интегральной чувствительности фотоэлемента 1. Рассчитать интегральную чувствительность фотоэлемента по формуле (7.9), где S = 4 см2:
2. Вычислить gср., найти погрешность Δγ. Результаты вычислений занести в таблицу 7.2. Сделать выводы.
Таблица 7. 2
Новая установка Приборы и оборудование: установка для изучения явления фотоэффекта.
Методика измерений
Из (7.2) и (7.3) получим:
График зависимости U З= f (n) представляет собой прямую:
с угловым коэффициентом
Точка пересечения графика с осью абсцисс даёт значение красной границы фотоэффекта n0.
Экспериментальная установка
Экспериментальная установка для изучения фотоэффекта состоит из объекта исследования (блок 1 на рис.7.5) и измерительного устройства 2, выполненных в виде конструктивно законченных изделий. Блок 1 выполнен в виде сборного корпуса, в котором установлены осветитель – ртутная лампа 3 с источником питания, блок светофильтров 4 и устройство регулировки освещённости 5. Положение «0» блока светофильтров соответствует прохождению света без светофильтров, а в положении «5» световой поток полностью перекрывается. На передней панели расположены регуляторы 6 баланса усилителя «Грубо» и «Точно».
На передней панели измерительного устройства 2 размещены органы управления и индикации: кнопка 8 «прямая-обратная» с соответствующими индикаторами предназначена для включения режима измерений; кнопки «+» и «–» – для регулировки напряжения; кнопка 7 «сброс» – для сброса напряжения на нуль; напряжение и ток фотоэлемента фиксируют вольтметр и микроамперметр. Порядок выполнения работы Задание 1. Измерение вольтамперной характеристики фотоэлемента. 1. Ознакомиться с установкой. 2. Включить установку в сеть; для этого подключить сетевые шнуры к сети, включить тумблеры «сеть» на левой боковой стенке блока 1 и на задней панели измерительного блока 2. 3. Диск со светофильтрами 4 установить в положение «5» и после 5-минутного прогрева ручками 6 установить нулевое значение тока микроамперметра при нулевом значении напряжения. 4. Поворотный диск 5 осторожно повернуть до упора против часовой стрелки. 5. Кнопкой 8 выбрать прямой режим. 6. Установить светофильтр 1 поворотом диска 4 до лёгкого щелчка фиксатора. 7. Кнопкой «сброс» установить нулевое значение напряжения. 8. Записать в табл.7.3 значения напряжения U и тока I. 9. Кнопками «+» и «-» устанавливать нужные значения напряжения U на фотоэлементе (см. табл.7.3) и измерять соответствующую силу тока I. 10. При достижении максимального напряжения нажать кнопку «сброс». 11. Измерения по пунктам 9 и 10 повторить для светофильтров 2, 3 и 4. Все данные записать в таблицу 7.3. Таблица
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 922; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.103 (0.017 с.) |

 . (6.1)
. (6.1) (6.2)
(6.2) . (6.2а)
. (6.2а) (6.3)
(6.3) , показывающая, какую долю энергии падающего излучения в интервале длин волн [ l; l+ d l] тело поглощает, называется спектральной поглощательной способностью тела. Тело называется абсолютно чёрным (АЧТ), если поглощает всё излучение, падающее на него: для абсолютно черного тела
, показывающая, какую долю энергии падающего излучения в интервале длин волн [ l; l+ d l] тело поглощает, называется спектральной поглощательной способностью тела. Тело называется абсолютно чёрным (АЧТ), если поглощает всё излучение, падающее на него: для абсолютно черного тела  .
. В природе не существует абсолютно чёрных тел. Тела, покрытые сажей или платиновой чернью, приближаются по своим свойствам к абсолютно черным лишь в ограниченном интервале длин волн.
В природе не существует абсолютно чёрных тел. Тела, покрытые сажей или платиновой чернью, приближаются по своим свойствам к абсолютно черным лишь в ограниченном интервале длин волн. . (6.4)
. (6.4) . Таким образом, универсальная функция Кирхгофа e(l,Т) есть монохроматическая интенсивность излучения абсолютно черного тела.
. Таким образом, универсальная функция Кирхгофа e(l,Т) есть монохроматическая интенсивность излучения абсолютно черного тела. Для тел, не являющихся абсолютно чёрными,
Для тел, не являющихся абсолютно чёрными, . (6.5)
. (6.5) . (6.6)
. (6.6) . (6.7)
. (6.7) 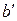 =1.29.10-5
=1.29.10-5  .
. «Ультрафиолетовая катастрофа». Несмотря на детальное изучение характеристик теплового излучения, математический вид функции e(l,Т) долгое время оставался для физиков загадкой. Английские учёные Дж.Рэлей и Дж.Джинс попытались теоретически вывести зависимость e(l,Т), исходя из теоремы классической статистики о равнораспределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия, равная двум половинкам kT – одна половинка на электрическую, вторая – на магнитную энергию волны (по классическим представлениям на каждую степень свободы приходится в среднем энергия, равная kT /2), то есть средняя энергия осциллятора
«Ультрафиолетовая катастрофа». Несмотря на детальное изучение характеристик теплового излучения, математический вид функции e(l,Т) долгое время оставался для физиков загадкой. Английские учёные Дж.Рэлей и Дж.Джинс попытались теоретически вывести зависимость e(l,Т), исходя из теоремы классической статистики о равнораспределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия, равная двум половинкам kT – одна половинка на электрическую, вторая – на магнитную энергию волны (по классическим представлениям на каждую степень свободы приходится в среднем энергия, равная kT /2), то есть средняя энергия осциллятора . (6.9)
. (6.9) (6.10)
(6.10) . Полная энергетическая светимость по формуле Рэлея-Джинса также равна бесконечности. С точки зрения классической физики вывод формулы Рэлея-Джинса безупречен, но она оказалась неверна.
. Полная энергетическая светимость по формуле Рэлея-Джинса также равна бесконечности. С точки зрения классической физики вывод формулы Рэлея-Джинса безупречен, но она оказалась неверна. , (6.11)
, (6.11) , (6.12)
, (6.12) . (6.13)
. (6.13) , (6.14)
, (6.14) . (6.14а)
. (6.14а) осциллятора Планк, подобно Рэлею, воспользовался законом классической статистики, он получил бы из (6.13) и (6.9) формулу Рэлея-Джинса (5.10).
осциллятора Планк, подобно Рэлею, воспользовался законом классической статистики, он получил бы из (6.13) и (6.9) формулу Рэлея-Джинса (5.10). , (6.15)
, (6.15) (6.16)
(6.16) . Кроме того, формула Планка удовлетворяет принципу соответствия – в области малых частот, когда hν<<kT, (6.14) переходит в формулу Рэлея-Джинса.
. Кроме того, формула Планка удовлетворяет принципу соответствия – в области малых частот, когда hν<<kT, (6.14) переходит в формулу Рэлея-Джинса. . Если температура тела Т1 отличается от температуры среды Т2, то излучение не будет равновесным, и энергия, излучаемая в окружающую среду единицей площади тела в единицу времени, определяется разностью:
. Если температура тела Т1 отличается от температуры среды Т2, то излучение не будет равновесным, и энергия, излучаемая в окружающую среду единицей площади тела в единицу времени, определяется разностью: . (6.18)
. (6.18) . (6.18а)
. (6.18а) , (6.19)
, (6.19) . (6.20)
. (6.20) Схема пирометра изображена на рис.6.5. Основные части пирометра: 1 - объектив; 2 - окуляр; 3 - пирометрическая лампа. Через окуляр пирометра имеется возможность наблюдать яркость накала нити на фоне раскаленного тела, температуру которого требуется определить.
Схема пирометра изображена на рис.6.5. Основные части пирометра: 1 - объектив; 2 - окуляр; 3 - пирометрическая лампа. Через окуляр пирометра имеется возможность наблюдать яркость накала нити на фоне раскаленного тела, температуру которого требуется определить. Перед окуляром находится красный светофильтр 6, выделяющий из спектров обоих источников излучение определенной длины волны. Ток накала нити пирометрической лампы регулируется реостатом 8 при помощи поворота кольца 5. Можно добиться такого накала нити, при котором она перестает быть видимой, исчезает на фоне раскаленного тела. Измеряемая температура отсчитывается по шкале 4. При изготовлении пирометр градуируется по излучению абсолютно черного тела.
Перед окуляром находится красный светофильтр 6, выделяющий из спектров обоих источников излучение определенной длины волны. Ток накала нити пирометрической лампы регулируется реостатом 8 при помощи поворота кольца 5. Можно добиться такого накала нити, при котором она перестает быть видимой, исчезает на фоне раскаленного тела. Измеряемая температура отсчитывается по шкале 4. При изготовлении пирометр градуируется по излучению абсолютно черного тела. 3. Вращая кольцо реостата пирометра, добиться исчезновения нити пирометра на фоне исследуемой лампы (рис.6.6, в).
3. Вращая кольцо реостата пирометра, добиться исчезновения нити пирометра на фоне исследуемой лампы (рис.6.6, в).

 . (7.2)
. (7.2) . (7.3)
. (7.3) . (7.4)
. (7.4) и связанная с нею длина волны
и связанная с нею длина волны  :
: (7.5)
(7.5) , (7.6)
, (7.6) . (7.7)
. (7.7) , (7.8)
, (7.8) . (7.9)
. (7.9)
 силы света, излучаемого в направлении нормали с
силы света, излучаемого в направлении нормали с 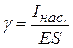 . (7.9)
. (7.9)
 . (7.6)
. (7.6) (7.7)
(7.7) . Таким образом, по графику (рис.7.4) можно экспериментально определить постоянную Планка:
. Таким образом, по графику (рис.7.4) можно экспериментально определить постоянную Планка: . (7.8)
. (7.8)



