
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение зависимости электрического сопротивления металлов и полупроводников от температуры. Определение энергии активации полупроводников.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель работы: исследование отличительных особенностей в свойствах металлов и полупроводников. Измерение энергии активации полупроводников.
Теоретическое введение При объединении атомов в кристаллическое тело структура энергетических уровней электронов претерпевает важные изменения. Эти изменения почти не затрагивают наиболее глубокие уровни, образующие внутренние, заполненные оболочки. Зато наружные уровни коренным образом перестраиваются. Указанное различие связано с разным пространственным распределением электронов, находящихся на глубоко лежащих и на верхних энергетических уровнях. Атомы в кристалле тесно «прижаты» друг к другу. Волновые функции наружных электронов в существенной мере перекрываются, что приводит к обобществлению этих электронов – они теперь принадлежат не отдельным атомам, а всему кристаллу. В то же время волновые функции внутренних электронов друг с другом практически не перекрываются. Положение этих уровней в кристалле мало отличается от их положения у изолированных атомов.
Ширина зон определяется величиной связи между атомами и не зависит от числа атомов в кристалле. В то же время количество уровней в зоне равно числу атомов и описывается цифрами с десятком или даже с несколькими десятками нулей. Таким образом, расстояние между уровнями оказывается столь незначительным, что говорить о положении отдельных уровней в зоне не имеет смысла. В то же время количество уровней сохраняет вполне ясный смысл, так как при сближении атомов число возможных состояний (а, следовательно, и число электронов, которые могут занять эти состояния) не изменяется. Электропроводность твердых тел определяется распределением электронов по уровням (рис.16.2). В металлах электроны лишь частично заполняют последнюю из занимаемых зон (зона проводимости – ЗП), и в ней имеются свободные состояния. В присутствии электрического поля электроны проводимости могут занимать эти состояния, и металл проводит электрический ток. В изоляторах (диэлектриках) электроны доверху заполняют последнюю из занятых зон (валентную зону – ВЗ). Следующая разрешенная зона (зона проводимости) не содержит электронов. В присутствии поля ни один из электронов не может изменить своего состояния, так как нет свободных энергетических состояний. Твердое тело будет не проводящим при температуре, равной Т =0 К. Однако при отличной от нуля температуре существует конечная вероятность того, что некоторые электроны будут за счет теплового возбуждения переброшены через энергетическую щель (Е g – ширина запрещенной зоны – ЗЗ) из валентной зоны в зону проводимости. При этом остаются незанятые уровни в валентной зоне. Термически возбужденные электроны способны переносить ток (переходить на свободные энергетические состояния в зоне проводимости). В валентной зоне проводимость становится возможной из-за появления свободных состояний – дырок, которые ведут себя как свободные носители положительного заряда: ближайший к дырке электрон валентной зоны, попадая в неё, оставляет при этом новую дырку, которую заполнит другой электрон валентной зоны и т.д. Дырка валентной зоны будет перемещаться по кристаллу в направлении, противоположном направлению движения электронов валентной зоны. Таким образом, валентная зона будет зоной дырочной проводимости. Приведут ли тепловые перебросы электронов из валентной зоны в зону проводимости к заметной проводимости или нет, существенно зависит от ширины запрещенной зоны Е g, поскольку число электронов, переброшенных в зону проводимости при температуре Т, пропорционально величине Твердые тела, которые являются диэлектриками при Т =0 К, но имеют такую ширину запрещенной зоны Е g, что тепловое возбуждение при температурах ниже точки плавления может обуславливать заметную проводимость, называются полупроводниками. Ясно, что не существует четкого различия между полупроводниками и диэлектриками; грубо говоря, в наиболее важных полупроводниках Е g обычно меньше 2 эВ, а часто составляет лишь несколько десятых электрон-вольта. Типичные удельные сопротивления полупроводников при комнатной температуре лежат в интервале между 10-5 и 107 Ом∙м (в отличие от металлов, где ρ=10-8 Ом∙м, а также и от хороших диэлектриков, у которых ρ может достигать до 1020 Ом∙м). Самой важной характеристикой любого полупроводника при температуре Т является число n c электронов в зоне проводимости, приходящееся на единицу объема, и число дырок p v на единицу объема в валентной зоне. Эти величины определяются произведением числа уровней, имеющихся в единице объема полупроводника, на вероятность их заполнения. Вероятность заполнения энергетических уровней выражается функцией распределения Ферми f (E). Для анализа электронных состояний необходимо использовать квантовую статистику
где Е – энергии уровней; μ – химический потенциал. Часто химический потенциал полупроводников называется «уровнем Ферми» (μ= E F). Однако, это неудачная терминология. Обычное определение уровня Ферми – энергия, ниже которой при Т =0 К в металле электронные уровни в зоне проводимости заполнены, а выше – свободны (не заполнены). В полупроводниках химический потенциал μ лежит примерно в середине запрещенной зоны, поэтому ни один электронный уровень не совпадает с химическим потенциалом. Обозначим через Е с энергию дна зоны проводимости, а через Е v – энергию потолка валентной зоны (рис. 16.3). В полупроводниках даже при весьма малой ширине запрещенной зоны Е g= Е с– Е v обычно выполняется условие
Так что число электронов n c в зоне проводимости, приходящееся на единицу объема, будет равно
где А (Т) – число уровней, имеющихся в зоне проводимости в единице объема полупроводника. Вероятность появления дырки в валентной зоне определяется разностью:
поскольку
Заметим, что А (Т) и В (Т) – медленно меняющиеся функции температуры по сравнению с экспонентами в (16.4) и (16.5). Если полупроводник является настолько чистым, что примеси вносят пренебрежимо малый вклад в концентрацию носителей, то мы имеем дело с собственным полупроводником. В нем электроны могут попасть в зону проводимости, только покинув заполненные ранее уровни в валентной зоне, оставив вместо себя там дырки. Таким образом, число электронов в зоне проводимости равно числу дырок в валентной зоне n c(T)= p v(T)= n. Так что из (16.4) и (16.5) можно записать
Найдем теперь электропроводность полупроводника. В присутствии поля большая часть электронов в зоне проводимости начинает двигаться в сторону, противоположную полю. Средняя величина скорости электронов перестает быть равной нулю и направлена вдоль поля. При этом вплоть до самых сильных полей (практически до пробоя) выполняется формула
где
где j – плотность электрического тока,
где предэкспоненциальный множитель заменен константой D. Измерим электропроводность σ как функцию температуры и изобразим результаты на графике в полулогарифмическом масштабе:
Формула (16.9) показывает, что график должен иметь вид прямой линии с наклоном Е g/2 k. Наклон прямой позволяет, таким образом, определить ширину запрещенной зоны Е g. Приведенные соображения верны лишь постольку, поскольку электропроводность полупроводника определяется переходами электронов из валентной зоны в зону проводимости, то есть пока основной вклад в электропроводность вносит собственная проводимость полупроводника. При небольших температурах это обычно не имеет места, так как полупроводники всегда содержат примеси.
При тепловом возбуждении гораздо легче вызвать переход электрона в зону проводимости с донорного уровня или на акцепторный уровень из валентной зоны, чем переход через всю запрещенную зону из валентной зоны в зону проводимости. Поэтому при низких температурах именно примеси определяют температурный ход электропроводности полупроводника. На рис. 16.5 представлена зависимость
Здесь  – энергия активации донорного уровня, имеющего энергию Е d. В области низких температур угловой коэффициент прямолинейного участка – энергия активации донорного уровня, имеющего энергию Е d. В области низких температур угловой коэффициент прямолинейного участка  определяется шириной энергетического зазора между донорным уровнем и зоной проводимости. В области высоких температур наклон графика к оси абсцисс определяется шириной запрещённой зоны: определяется шириной энергетического зазора между донорным уровнем и зоной проводимости. В области высоких температур наклон графика к оси абсцисс определяется шириной запрещённой зоны:  . .
Итак, наиболее яркая особенность полупроводника состоит в том, что у них в отличие от металлов электросопротивление падает с ростом температуры. В металлах температурный коэффициент удельного сопротивления
положителен, и его можно считать приближенно постоянным, если интервал изменения температуры достаточно мал. Так, если
В классической электронной теории металлов предполагается, что движение электронов подчиняется законам классической механики Ньютона. Электроны проводимости рассматриваются как электронный газ, подобный идеальному газу в молекулярной физике. Предполагается, что причина электрического сопротивления заключается в соударениях электронов с положительными ионами решетки металла. В действительности же электроны проводимости подчиняются законам квантовой механики, и для них справедлива квантовая статистика – их распределение по энергиям определяется функцией Ферми (16.1). И оказывается, что причина сопротивления чистых металлов – взаимодействие электронов с колебаниями решетки. В квантовой теории кристаллических твердых тел кванты колебаний решетки были названы фононами. Электросопротивление чистых металлов возникает из-за столкновений электронов с фононами. Расчеты показывают, что при высоких температурах (Т >θD) ρ~ Т, что и наблюдается экспериментально. Здесь θD – дебаевская температура металла. Экспериментальная часть Приборы и оборудование: исследуемые образцы (металл, полупроводник), нагревательная печь, термометр, вольтметр, амперметр, выпрямительный мост. Методика измерений Температурная зависимость сопротивления полупроводника определяется формулой (см. (16.9)):
где Е g – ширина запрещенной зоны, k – постоянная Больцмана, R 0 – постоянная величина, характеризующая свойства полупроводника (R 0= R при Т→¥). Проведя логарифмирование (16.13), получим:
График зависимости
Сопротивление R вычисляется из опытных данных по закону Ома:
где I – измеренный ток, U – напряжение. Температурный коэффициент сопротивления металла можно определить, используя формулу (16.12):
где R 0 – сопротивление металлического образца при t=00С.
Экспериментальная установка
Порядок выполнения работы Внимание! Нагрев начинается сразу после включения установки в сеть. Заранее подготовьте таблицы для записи опытных данных. 1. Установите тумблер 6 в нижнее положение (полупроводник). 2. Включите установку в сеть. 3. Измерьте и запишите в табл.16.1 температуру t, силу тока I и напряжение U.
Таблица 16.1
4. Переключите тумблер 6 вверх (металл). 5. Запишите значения I и U при той же температуре. 6. Когда температура достигнет 300С, снова измерьте и запишите значения I и U для обоих образцов. 7. Измеряйте и записывайте значения тока и напряжения при температурах, указанных в табл.16.1. 8. Отключите установку от сети. 9. Для каждой температуры вычислите сопротивление обоих образцов по формуле (16.16). 10. Для полупроводника определите lnR и 11. Постройте графики зависимостей: R = f (T) – для обоих образцов и 12. По графику R = f (T) для металла определите R 0 – сопротивление при t =00C и вычислите температурный коэффициент сопротивления αм по формуле (16.12б). 13. Используя график зависимости 14. Оцените погрешности вычисленных величин αм и
Контрольные вопросы 1. Как объясняет зонная теория деление твердых тел на металлы, полупроводники и диэлектрики? 2. Что такое валентная зона? Зона проводимости? Запрещенная зона? Как они образуются? 3. Сформулируйте принцип Паули. 4. Запишите формулу статистического распределения Ферми-Дирака (16.1). Как из неё можно получить зависимость сопротивления полупроводника от температуры? 5. Объясните механизм собственной проводимости в полупроводниках. 6. Как зависит сопротивление полупроводника от температуры и почему? 7. Что такое энергия активации? 8. Нарисуйте график зависимости lns от 1/Т для собственной и примесной проводимости. 9. Объясните методику определения ширины запрещенной зоны (энергии активации) полупроводника. 10. Как зависит сопротивление металла от температуры и почему?
Используемая литература [1] §§ 43.1, 43.2, 43.3, 43.4, 43.5; [2] §§ 13.11, 40.1, 40.2, 40.3, 40.6; [3] §§ 4.42, 4.43, 4.45, 4.46, 4.48, 4.49, 4.50, 4.51, 4.52; [5] § 26; [6] §§ 39, 40, 42, 43; [7] §§ 98, 238, 240, 241, 242, 243.
Лабораторная работа 3-17 Эффект Холла Цель работы: определение постоянной Холла (R), концентрации (n), знака носителей заряда в полупроводнике и их подвижности (u).
Теоретическое введение
В 1880 г. американский физик Э.Г.Холл впервые описал эффект, впоследствии названный его именем. Явление, открытое Холлом, состоит в том, что в проводнике с током, помещённом в магнитное поле, перпендикулярное направлению тока, возникает электрическое поле в направлении, перпендикулярном направлениям тока и магнитного поля. Для наблюдения явления Холла образец помещают между полюсами сильного электромагнита, создающего магнитную индукцию порядка 1 Вб/м2, а возникающую разность потенциалов измеряют с помощью чувствительного гальванометра (рис.17.1).
Опыт показывает, что поперечная разность потенциалов UH пропорциональна плотности тока j, магнитной индукции В и расстоянию d (толщине пластины):
где R – постоянная Холла. Простое объяснение явления Холла даёт классическая электронная теория, которая объясняет появление электрического поля вдоль оси OY действием силы Лоренца. Будем приближённо считать, что все электроны движутся с постоянной скоростью, равной средней скорости их упорядоченного движения v (дрейфовая скорость). Тогда на каждый электрон действует сила Лоренца, перпендикулярная направлению тока и магнитного поля и равная
Эта сила отклоняет электроны в отрицательном направлении оси OY (дрейфовая скорость электронов направлена против тока – см. рис.17.1). Однако электроны не могут долго двигаться в направлении оси OY, поскольку они достигают границы проводника (грани пластины). По мере того как они там скапливаются, нарастает электрическое поле Е, направленное вдоль оси OY, и оно противодействует движению и дальнейшему накоплению электронов. В состоянии равновесия действие этого поперечного поля Еy компенсирует силу Лоренца:
и ток идёт лишь в направлении оси OX. Поэтому поперечная разность потенциалов
В этом выражении среднюю скорость электронов v можно выразить через плотность тока j, так как
где n – концентрация электронов в проводнике. Из (17.4) и (17.5) получим:
Полученное в рамках классической электронной теории выражение (17.6) совпадает с опытными данными (17.1), а постоянная Холла R оказывается равной
Она зависит от концентрации электронов n, и поэтому, измеряя постоянную Холла, можно определить концентрацию электронов в проводнике. Видно также, что знак поперечной разности потенциалов зависит от знака носителей заряда. Этот вывод очень важен, поскольку он означает, что измерения поля Холла позволяют определить знак носителей заряда. Экспериментальные данные, впервые полученные Холлом, находились в согласии со знаком заряда электрона, определённым позднее в 1897 г. Томсоном. Следует отметить, что лишь для щелочных металлов постоянная Холла соответствует предсказаниям теории свободных электронов. В некоторых металлах даже знак постоянной Холла положительный. Объясняет это лишь квантовая теория твёрдых тел. Заметим ещё, что в 1985 г. К.Клитцингу была присуждена Нобелевская премия по физике за открытие квантового эффекта Холла в кремниевых структурах металл-окисел-полупроводник. Но это совсем другая история. Методика измерений Сила тока через образец I=jS, где S=аd – площадь сечения пластинки, а – ширина пластинки. Тогда из (17.6) получим Холловскую разность потенциалов:
где а =3.10-4 м. По закону Ома в дифференциальной форме плотность тока j прямо пропорциональна напряженности электрического поля E: j= s E, где s – удельная электропроводимость. С учетом (17.5):
Здесь u= v /E – подвижность зарядов, численно равная средней скорости направленного движения зарядов в электрическом поле с напряженностью, равной 1 В/м. Зная удельную электропроводимость образца (s=0.13(Ом.м)-1), можно вычислить из экспериментальных данных постоянную Холла по формуле (17.9) и рассчитать величину подвижности:
Экспериментальная часть Приборы и оборудование: измерительный блок и объект исследования. Измерительная установка Внешний вид установки представлен на рис.17.2. Измерительный блок формирует и регулирует силу тока электромагнита I эм и преобразователя (ток через образец) I, изменяет полярность тока. Ток преобразователя и электромагнита изменяются в пределах соответственно 0÷5 мА и 0÷10 мА. Объект исследования состоит из полупроводникового преобразователя Холла и электромагнита. Порядок выполнения работы 1. Включить установку (переключатель «сеть» находится на задней панели измерительного блока). 2. Переключателем измерителя переключить миллиамперметр в режим измерения тока через датчик Холла (при этом должен загореться соответствующий светодиод). 3. Установить полярность «+» переключателем «направление тока» (в индикации миллиамперметра отсутствует знак «–»). 4. Кнопками регулировки силы тока «+» и «–» установить силу тока через датчик Холла I =3 мА.
6. Установить полярность «+» переключателем «направление тока» (в индикации миллиамперметра отсутствует знак «–»). 7. Кнопками регулировки силы тока «+» и «–» установить силу тока электромагнита I эм=3 мА. 8. Измерить ЭДС Холла U +, записать все величины в таблицу 17.1. 9. Кнопками регулировки силы тока «+» и «–» устанавливать силу тока электромагнита I эм=4 мА; 5 мА; … 10 мА, каждый раз измеряяи записывая величину U +. 10. Установить полярность «–» переключателем «направление тока» (в индикации миллиамперметра присутствует знак «–»). 11. Повторить пункты 7-9, записывая в таблицу ЭДС Холла U – при другом направлении магнитного поля. 12. Повторить измерения ЭДС Холла для тока через датчик I =4 мА (пункты 2-11), а затем для I =5 мА. 13. По формуле (15.9) вычислите Холловскую разность потенциалов для каждого измерения. Результаты занесите в таблицу 17.1. U х=(U + – U –)/2. (17.12) 14. По графику (рис.17.3) зависимости В от I эм определите В и занесите в таблицу 17.1. 15. По формуле (17.9) рассчитайте R для каждого значения В, определяемого по току через электромагнит. 16. Вычислите среднее значение R. Таблица 17.1
17. Используя среднее значение R, определите концентрацию носителей заряда n по формуле (17.7). 18. По формуле (17.11) вычислите подвижность носителей заряда u. 19. Вычислите погрешности R и u.
Контрольные вопросы 1. В чем заключается эффект Холла? 2. Чем объясняется эффект Холла? 3. Чему равна и как направлена сила Лоренца? 4. Для каких целей практически используется эффект Холла? 5. Выведите формулу для Холловской разности потенциалов. 6. Как расположены эквипотенциальные поверхности при прохождении постоянного тока через образец: а) в отсутствие магнитного поля; в) при включенном магнитном поле? 7. Как исключается погрешность, связанная с несимметричностью контактов подключения миллиамперметра к образцу? 8. Каков знак носителей тока в изучаемом образце? Используемая литература
[1] §§ 21.2, 23.2; [2] §§ 14.2, 14.5; [5] § 45; [7] §§ 114, 117.
Лабораторная работа 3-18
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 У одиночных атомов одного и того же элемента энергия соответствующих уровней в точности одинакова. При сближении атомов эти уровни начинают расходиться, как это изображено на рис. 16.1. Расщепление энергетических уровней аналогично расхождению частот колебаний, происходящему при появлении связи между одинаковыми маятниками или между электрическими колебательными контурами, настроенными на одну и ту же частоту. Системы «разошедшихся» уровней образуют в кристалле разрешенные энергетические зоны, разделенные запрещенными зонами (рис. 16.1).
У одиночных атомов одного и того же элемента энергия соответствующих уровней в точности одинакова. При сближении атомов эти уровни начинают расходиться, как это изображено на рис. 16.1. Расщепление энергетических уровней аналогично расхождению частот колебаний, происходящему при появлении связи между одинаковыми маятниками или между электрическими колебательными контурами, настроенными на одну и ту же частоту. Системы «разошедшихся» уровней образуют в кристалле разрешенные энергетические зоны, разделенные запрещенными зонами (рис. 16.1).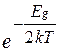 (k =1.38∙10-23 Дж/К – постоянная Больцмана). При Е g=4 эВ (1эВ=1.6∙10-19 Дж) эта величина при комнатной температуре (kT ≈0.025 эВ) составляет
(k =1.38∙10-23 Дж/К – постоянная Больцмана). При Е g=4 эВ (1эВ=1.6∙10-19 Дж) эта величина при комнатной температуре (kT ≈0.025 эВ) составляет  , то есть по сути дела переброса электронов в валентную зону не происходит. Если же Е g=0.25 эВ, то число переброшенных электронов при комнатной температуре определяется величиной
, то есть по сути дела переброса электронов в валентную зону не происходит. Если же Е g=0.25 эВ, то число переброшенных электронов при комнатной температуре определяется величиной  , так что будет наблюдаться заметная проводимость.
, так что будет наблюдаться заметная проводимость. , (16.1)
, (16.1) . (16.2)
. (16.2) Тогда благодаря тому, что каждый уровень электрона в зоне проводимости лежит выше Е с, а каждый уровень валентной зоны – ниже Е v, упрощается выражение для функции распределения f (Е) – оно становится классическим (статистика Больцмана).
Тогда благодаря тому, что каждый уровень электрона в зоне проводимости лежит выше Е с, а каждый уровень валентной зоны – ниже Е v, упрощается выражение для функции распределения f (Е) – оно становится классическим (статистика Больцмана). ; Е > Е с. (16.3)
; Е > Е с. (16.3) , (16.4)
, (16.4) ,
, и
и  . Поэтому число дырок p v в валентной зоне, приходящееся на единицу объема, будет равно
. Поэтому число дырок p v в валентной зоне, приходящееся на единицу объема, будет равно . (16.5)
. (16.5)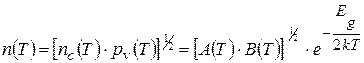 . (16.6)
. (16.6) , (16.7)
, (16.7) – среднее значение скорости электронов; Е – напряженность электрического поля;
– среднее значение скорости электронов; Е – напряженность электрического поля;  – коэффициент пропорциональности, носящий название подвижности электронов. Применяя формулу (16.7) к электронам в зоне проводимости и к дыркам в валентной зоне, найдем электропроводность:
– коэффициент пропорциональности, носящий название подвижности электронов. Применяя формулу (16.7) к электронам в зоне проводимости и к дыркам в валентной зоне, найдем электропроводность: , (16.8)
, (16.8) – подвижность дырок. Подставляя в (16.8) значение n c= p v= n из (16.6), получим:
– подвижность дырок. Подставляя в (16.8) значение n c= p v= n из (16.6), получим: , (16.9)
, (16.9) .
. Если примеси поставляют существенную часть электронов проводимости и (или) дырок валентной зоны, то мы имеем дело с несобственным полупроводником. Примеси, которые вносят вклад в концентрацию носителей тока, называются донорными, если они поставляют дополнительные электроны в зону проводимости, и акцепторными, когда они поставляют дополнительные дырки в валентную зону (то есть захватывают оттуда электроны). Донорные примеси – это атомы с более высокой валентностью, чем атомы чистого полупроводника (вещество-матрица), а акцепторы – атомы с более низкой валентностью. Самая важная информация о донорных и акцепторных уровнях заключается в том, что они лежат вблизи границ запрещенной зоны. На рис. 16.4 изображены энергетические диаграммы донорного (а) и акцепторного (б) полупроводника.
Если примеси поставляют существенную часть электронов проводимости и (или) дырок валентной зоны, то мы имеем дело с несобственным полупроводником. Примеси, которые вносят вклад в концентрацию носителей тока, называются донорными, если они поставляют дополнительные электроны в зону проводимости, и акцепторными, когда они поставляют дополнительные дырки в валентную зону (то есть захватывают оттуда электроны). Донорные примеси – это атомы с более высокой валентностью, чем атомы чистого полупроводника (вещество-матрица), а акцепторы – атомы с более низкой валентностью. Самая важная информация о донорных и акцепторных уровнях заключается в том, что они лежат вблизи границ запрещенной зоны. На рис. 16.4 изображены энергетические диаграммы донорного (а) и акцепторного (б) полупроводника.
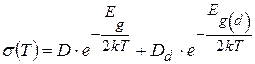 . (16.10)
. (16.10)
 (16.11)
(16.11) есть удельное сопротивление при 00С, а
есть удельное сопротивление при 00С, а  – его значение при t 0С, то можно положить
– его значение при t 0С, то можно положить . (16.12)
. (16.12) (16.13)
(16.13) . (16.14)
. (16.14)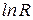 от
от  является прямой линией с угловым коэффициентом
является прямой линией с угловым коэффициентом  (рис.16.6). Определив тангенс угла наклона прямой к оси абсцисс, можно найти энергию активации (ширину запрещённой зоны) полупроводника:
(рис.16.6). Определив тангенс угла наклона прямой к оси абсцисс, можно найти энергию активации (ширину запрещённой зоны) полупроводника:
 . (16.15)
. (16.15) , (16.16)
, (16.16) , (16.12а)
, (16.12а) , (16.12б)
, (16.12б) Схема экспериментальной установки представлена на рис.16.7. Образцы помещены внутри нагревательной печи 1. Температура измеряется ртутным термометром 2. Печь подключается через индуктивное сопротивление 3 к сети переменного напряжения 220 В. Через образцы 4, соединённые последователь‑
Схема экспериментальной установки представлена на рис.16.7. Образцы помещены внутри нагревательной печи 1. Температура измеряется ртутным термометром 2. Печь подключается через индуктивное сопротивление 3 к сети переменного напряжения 220 В. Через образцы 4, соединённые последователь‑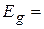
 – для полупроводника.
– для полупроводника. по формуле (16.15). Выразите её в джоулях и электрон-вольтах.
по формуле (16.15). Выразите её в джоулях и электрон-вольтах.
 , (17.1)
, (17.1) . (17.2)
. (17.2) , (17.3)
, (17.3) будет равна:
будет равна: . (17.4)
. (17.4) , (17.5)
, (17.5) . (17.6)
. (17.6) . (17.7)
. (17.7) , (17.8)
, (17.8) , (17.9)
, (17.9)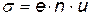 . (17.10)
. (17.10) . (17.11)
. (17.11) 5. Переключателем измерителя переключить миллиамперметр в режим измерения тока электромагнита (при этом должен загореться соответствующий светодиод).
5. Переключателем измерителя переключить миллиамперметр в режим измерения тока электромагнита (при этом должен загореться соответствующий светодиод).



