
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параллельное соединение сопротивления, индуктивности и емкостиСодержание книги
Поиск на нашем сайте
Если к зажимам электрической цепи, состоящей из параллельно соединенных элементов r, L и С (рисунок 6.6), приложено синусоидальное напряжение  , то синусоидальный ток, проходящий через эту цепь, равен. , то синусоидальный ток, проходящий через эту цепь, равен. 
В соответствии с первым законом Кирхгофа
где
Выражение комплексной проводимости
Уравнение закона Ома в комплексной форме
12. Законы Кирхгофа. Первый закон Кирхгофа в комплексной форме
Второй закон Кирхгофа в комплексной форме
Рисунок. 7.1 Метод контурных токов Пример. Составим уравнения методом контурных токов(рисунок 7.2)
Решим их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найдем последние. Метод узловых потенциалов
Рисунок 7.3 Составим уравнения по методу узловых потенциалов для узлов а и в. Потенциал узла Токи ветвей выразим по закону Ома Мощности в цепях синусоидального тока Передача энергии w по электрической цепи, рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс. Интенсивность передачи или преобразования энергии называется мощностью р
Выражение для мгновенного значения мощности в электрических цепях имеет вид
Когда мгновенная мощность отрицательна (рисунок 8.1),, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника к источнику питания. Среднее за период значение мгновенной мощности называется активной мощностью.
Интенсивность обмена энергии принято характеризовать реактивной мощностью.
Она положительна при отстающем токе (индуктивная нагрузка- Баланс мощностей Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
Баланс соблюдается и для реактивных мощностей
“-” где знак “+” относится к индуктивным элементам Умножив (8.14) на “j” и сложив полученный результат с (8.13), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности)
Резонанс напряжений Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.
Для цепи на рисунке 11.1 имеет место
где
В зависимости от соотношения величин 1. В цепи преобладает индуктивность, т.е.
 . Этому режиму соответствует векторная диаграмма на рисунке 11.2,а. . Этому режиму соответствует векторная диаграмма на рисунке 11.2,а.
Рисунок 11.2 2. В цепи преобладает емкость, т.е. 3. Условие резонанса напряжений
При этом, как следует из (11.1) и (11.2), При резонансе напряжений ток в цепи наибольший Частотные характеристики последовательного колебательного контура Зависимость реактивного сопротивления контура от частоты
Рисунок 11.3 Рисунок 11.4 Зависимость полного сопротивления контура от частоты Зависимость Зависимости
Рисунок 11.5 Рисунок 11.6 Зависимость
Рисунок 11.7
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.2.191 (0.009 с.) |



 (6.11)
(6.11) - ток в сопротивлении (совпадает по фазе с напряжением
- ток в сопротивлении (совпадает по фазе с напряжением  );
); - ток в индуктивности (отстает от напряжения на -
- ток в индуктивности (отстает от напряжения на -  );
); - ток в емкости (опережает напряжение на
- ток в емкости (опережает напряжение на  . (6.12)
. (6.12) .
. .
.
 .
.

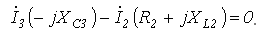






 ,
,  .
. Пример. Составим уравнения методом узловых потенциалов (рисунок 7.3).
Пример. Составим уравнения методом узловых потенциалов (рисунок 7.3). =0.
=0.
 .
. .
. .
.
 .
.
 .
.
 .
.
 ) и отрицательна при опережающем токе (емкостная нагрузка-
) и отрицательна при опережающем токе (емкостная нагрузка-  ). Единицу измерения реактивной мощности называют вольт-ампер реактивный (ВАр).
). Единицу измерения реактивной мощности называют вольт-ампер реактивный (ВАр).

 ; – к емкостным
; – к емкостным  .
. или
или


 ,
,
 .
.
 и
и  возможны три различных случая.
возможны три различных случая. , а, следовательно,
, а, следовательно,
 , а значит,
, а значит,  . Этот случай отражает векторная диаграмма на рисунке 11.2,б.
. Этот случай отражает векторная диаграмма на рисунке 11.2,б. - случай резонанса напряжений (рисунок 11.2,с).
- случай резонанса напряжений (рисунок 11.2,с). .
.
 .
. .
. (рисунок 11.3), где
(рисунок 11.3), где  ,
,  .
.

 ,
,  (рисунок 11.4).До резонанса характер сопротивления контура активно- емкостной, при резонансе активный, после резонанса активно- индуктивный.
(рисунок 11.4).До резонанса характер сопротивления контура активно- емкостной, при резонансе активный, после резонанса активно- индуктивный. - амплитудно - частотная характеристика (АЧХ),
- амплитудно - частотная характеристика (АЧХ),  (рисунок 11.5).
(рисунок 11.5).

 ,
,  ,
,  (рисунок 11.6).
(рисунок 11.6).

 - фазо- частотная характеристика (ФЧХ),
- фазо- частотная характеристика (ФЧХ), 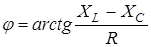 (рисунок 11.7).
(рисунок 11.7).



