
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синусоидальный ток напряжение эдсСтр 1 из 2Следующая ⇒
Законы Кирхгофа Первый закон Кирхгофа - алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю
Токи, направленные от узла, условно принимаются положительными, а направленные к нему – отрицательными (или наоборот). Второй закон Кирхгофа - алгебраическая сумма э. д. с. замкнутого контура равна алгебраической сумме падений напряжений в нём
П р и м е н е н и е з а к о н о в К и р х г о ф а. Устанавливаем число неизвестных токов, равное Nв — Nт. Для каждой ветви задаются положительным направлением тока. Общее число уравнений, составляемых по первому и второму законам Кирхгофа, равно числу (Nв — Nт) неизвестных токов. Числоуравнений, составляемых по первому закону Кирхгофа, равно (Nу - 1). Число взаимонезависимых уравнений, составляемых по второму закону Кирхгофа К =(Nв —Nт ) — (Nу - 1). (3.3) При составлении уравнений по второму закону Кирхгофа следует выбирать независимые контуры, не содержащие источников тока.
3. В основе принципа лежит принцип суперпозиции (наложения): ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности. Например, токи в схеме на рис. 1.10, а находятся как алгебраические суммы частичных токов, определяемых из схем 1.10, б и в.
Метод контурных токов Метод основан на том, что ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви. При пользовании этим методом выбирают и обозначают контурные токи (по любой ветви цепи должен проходить хотя бы один выбранный контурный ток). Общее число контурных токов равно К =(Nв —Nт ) — (Nу - 1). Рекомендуется выбирать Nт, контурных токов так, чтобы каждый из них - проходил через один источник тока. Эти контурные токи можно считать совпадающими с соответствующими токами источников тока J1, J2,. .., JNT, и они обычно являются заданными условиями задачи. Для них уравнения не составляют, но учитывают при составлении уравнений для других контуров. Оставшиеся К =(Nв —Nт ) — (Nу - 1)контурные токи выбирают проходящими по ветвям, не содержащим источников тока. Для определения последних контурных токов по второму закону Кирхгофа для этих контуров составляют К уравнений в виде
R11I11 + R12Ι22 + … +R1kIkk+ … + R21I11 + R22Ι22 + … +R2kIkk+ … + Rk1I11 + Rk2Ι22 + … +RkkIkk+ … + где Rnn — собственное сопротивление контура n (сумма сопротивлений всех ветвей, входящих в контур n); Rnl — общее сопротивление контуров n и L, причем Rnl = Rln.. Если направления контурных токов в общей ветви для n и L, совпадают, то Rnl положительно, в противном случае Rnl отрицательно; Еnn- алгебраическая сумма э. д. с., включенных в ветви, образующие контур n; Rn — общее сопротивление ветви контура n с контуром, содержащим источник тока Jn Метод узловых потенциалов. Он позволяет уменьшить количество уравнений системы до числа m = Nу - 1.(3.5) Сущность метода заключается в том, что вначале путем решения системы уравнений определяют потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, находят с помощью закона Ома. При составлении уравнений по методу узловых потенциалов вначале полагают равным нулю потенциал какого-либо узла (его называют базисным). Для определения потенциалов оставшихся (m = Nу —1) узлов составляется следующая система уравнений
Здесь Gss – сумма проводимостей ветвей, присоединённых к узлу S; Gsq – сумма проводимостей ветвей, непосредственно соединяющих узел S с узлом q;
Методом узловых потенциалов рекомендуется пользоваться в тех случаях, когда число уравнений будет меньше числа уравнений, составленных по методу контурных токов. Если в схеме некоторые узлы соединяются идеальными источниками э.д.с., то число m уравнений, составляемых по методу узловых потенциалов, уменьшается m = Nу – Nи – 1(3.7) где Nи – число ветвей, содержащих только идеальные источники э.д.с. В этом случае за нуль принимается один из узлов, принадлежащих ветви с идеальным источником э.д.с., тогда потенциал другого равен _± Е. Плюс, если двигаться по э.д.с., минус –если против.
6. Баланс мощностей Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи. Для любой замкнутой электрической цепи сумма мощностей РИ, развиваемых источниками электрической энергии, равна сумме мощностей Рп, расходуемых в приемниках энергии
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи. Следует указать, что в левой части (4.6) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (4.6) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора). Где Σ Εk Ik – алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия э.д.с. Εk и соответствующего тока Ik совпадают, в противном случае слагаемое отрицательно; Σ Εk Jk - алгебраическая сумма; здесь положительны те из слагаемых, для которых напряжение на источнике тока (оно определяется расчетом цепи внешней по отношению к зажимам источника тока) и его ток Jk совпадают по направлению, в противном случае слагаемое отрицательно. 12. Законы Кирхгофа. Первый закон Кирхгофа в комплексной форме
Второй закон Кирхгофа в комплексной форме
Рисунок. 7.1 Метод контурных токов Пример. Составим уравнения методом контурных токов(рисунок 7.2)
Решим их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найдем последние. Метод узловых потенциалов
Рисунок 7.3 Составим уравнения по методу узловых потенциалов для узлов а и в. Потенциал узла Токи ветвей выразим по закону Ома Баланс мощностей Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
Баланс соблюдается и для реактивных мощностей
“-” где знак “+” относится к индуктивным элементам Умножив (8.14) на “j” и сложив полученный результат с (8.13), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности)
Резонанс напряжений Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.
Для цепи на рисунке 11.1 имеет место
где
В зависимости от соотношения величин 1. В цепи преобладает индуктивность, т.е.
 . Этому режиму соответствует векторная диаграмма на рисунке 11.2,а. . Этому режиму соответствует векторная диаграмма на рисунке 11.2,а.
Рисунок 11.2 2. В цепи преобладает емкость, т.е. 3. Условие резонанса напряжений
При этом, как следует из (11.1) и (11.2), При резонансе напряжений ток в цепи наибольший Законы Кирхгофа Первый закон Кирхгофа - алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю
Токи, направленные от узла, условно принимаются положительными, а направленные к нему – отрицательными (или наоборот). Второй закон Кирхгофа - алгебраическая сумма э. д. с. замкнутого контура равна алгебраической сумме падений напряжений в нём
П р и м е н е н и е з а к о н о в К и р х г о ф а. Устанавливаем число неизвестных токов, равное Nв — Nт. Для каждой ветви задаются положительным направлением тока. Общее число уравнений, составляемых по первому и второму законам Кирхгофа, равно числу (Nв — Nт) неизвестных токов. Числоуравнений, составляемых по первому закону Кирхгофа, равно (Nу - 1). Число взаимонезависимых уравнений, составляемых по второму закону Кирхгофа К =(Nв —Nт ) — (Nу - 1). (3.3) При составлении уравнений по второму закону Кирхгофа следует выбирать независимые контуры, не содержащие источников тока.
3. В основе принципа лежит принцип суперпозиции (наложения): ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности. Например, токи в схеме на рис. 1.10, а находятся как алгебраические суммы частичных токов, определяемых из схем 1.10, б и в.
Метод контурных токов Метод основан на том, что ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви. При пользовании этим методом выбирают и обозначают контурные токи (по любой ветви цепи должен проходить хотя бы один выбранный контурный ток). Общее число контурных токов равно К =(Nв —Nт ) — (Nу - 1). Рекомендуется выбирать Nт, контурных токов так, чтобы каждый из них - проходил через один источник тока. Эти контурные токи можно считать совпадающими с соответствующими токами источников тока J1, J2,. .., JNT, и они обычно являются заданными условиями задачи. Для них уравнения не составляют, но учитывают при составлении уравнений для других контуров. Оставшиеся К =(Nв —Nт ) — (Nу - 1)контурные токи выбирают проходящими по ветвям, не содержащим источников тока. Для определения последних контурных токов по второму закону Кирхгофа для этих контуров составляют К уравнений в виде
R11I11 + R12Ι22 + … +R1kIkk+ … + R21I11 + R22Ι22 + … +R2kIkk+ … + Rk1I11 + Rk2Ι22 + … +RkkIkk+ … + где Rnn — собственное сопротивление контура n (сумма сопротивлений всех ветвей, входящих в контур n); Rnl — общее сопротивление контуров n и L, причем Rnl = Rln.. Если направления контурных токов в общей ветви для n и L, совпадают, то Rnl положительно, в противном случае Rnl отрицательно; Еnn- алгебраическая сумма э. д. с., включенных в ветви, образующие контур n; Rn — общее сопротивление ветви контура n с контуром, содержащим источник тока Jn Метод узловых потенциалов. Он позволяет уменьшить количество уравнений системы до числа m = Nу - 1.(3.5) Сущность метода заключается в том, что вначале путем решения системы уравнений определяют потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, находят с помощью закона Ома. При составлении уравнений по методу узловых потенциалов вначале полагают равным нулю потенциал какого-либо узла (его называют базисным). Для определения потенциалов оставшихся (m = Nу —1) узлов составляется следующая система уравнений
Здесь Gss – сумма проводимостей ветвей, присоединённых к узлу S; Gsq – сумма проводимостей ветвей, непосредственно соединяющих узел S с узлом q;
Методом узловых потенциалов рекомендуется пользоваться в тех случаях, когда число уравнений будет меньше числа уравнений, составленных по методу контурных токов. Если в схеме некоторые узлы соединяются идеальными источниками э.д.с., то число m уравнений, составляемых по методу узловых потенциалов, уменьшается m = Nу – Nи – 1(3.7) где Nи – число ветвей, содержащих только идеальные источники э.д.с. В этом случае за нуль принимается один из узлов, принадлежащих ветви с идеальным источником э.д.с., тогда потенциал другого равен _± Е. Плюс, если двигаться по э.д.с., минус –если против. 6. Баланс мощностей Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи. Для любой замкнутой электрической цепи сумма мощностей РИ, развиваемых источниками электрической энергии, равна сумме мощностей Рп, расходуемых в приемниках энергии
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи. Следует указать, что в левой части (4.6) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (4.6) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).
Где Σ Εk Ik – алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия э.д.с. Εk и соответствующего тока Ik совпадают, в противном случае слагаемое отрицательно; Σ Εk Jk - алгебраическая сумма; здесь положительны те из слагаемых, для которых напряжение на источнике тока (оно определяется расчетом цепи внешней по отношению к зажимам источника тока) и его ток Jk совпадают по направлению, в противном случае слагаемое отрицательно. синусоидальный ток напряжение эдс Величины е (1.1), u(1.2), i (1.3) называют мгновенными ЭДС, напряжением и током. Их наибольшие значения Еm, Umи Imназывают а амплитудами. Величину ω = 2π/Т = 2πfназывают угловой частотой. Аргумент синуса, отсчитываемый от ближайшей предыдущей точки перехода синусоидальной величины через нуль от отрицательных к положительным ее значениям, называют фазой, величины - начальной фазой, соответственно, ЭДС, напряжения и тока.
На рис. 1.1. изображены синусоидальные напряжение и ток с одним и тем же периодом.
Рис. 1.1. Синусоидальные напряжение и ток с одним и тем же периодом Необходимо обратить внимание на то, что положительные фазы Разность фаз напряжения и тока В большинстве случаев мы стремимся к тому, чтобы в электрических цепях токи и напряжения изменялись по синусоидальному закону, так как отклонение от этого закона ведет к нежелательным явлениям - появляются дополнительные потери в элементах цепи, возрастает влияние мощных линий передачи на соседние линии связи и т.д. Начнем рассмотрение с синусоидальных функций еще и потому, что любую периодическую функцию можно разложить в ряд синусоидальных функций различных частот (ряд Фурье) и, следовательно, рассмотрение синусоидальных токов позволит в дальнейшем перейти к изучению более сложных периодических ЭДС, токов и напряжений.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.142.189 (0.076 с.) |
 . ( 3.1)
. ( 3.1) .
.

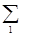 JnRn = Е11,
JnRn = Е11, JnRn = Е22, (3.4)
JnRn = Е22, (3.4) JnRn = Еkk
JnRn = Еkk 
 (3.6)
(3.6) - алгебраическая сумма произведений э.д.с. ветвей, примыкающих к узлу S, на их проводимости; при этом со знаком плюс берутся те э.д.с., которые действуют в направлении узла S, и со знаком минус –в направлении от узла S;
- алгебраическая сумма произведений э.д.с. ветвей, примыкающих к узлу S, на их проводимости; при этом со знаком плюс берутся те э.д.с., которые действуют в направлении узла S, и со знаком минус –в направлении от узла S; - алгебраическая сумма источников тока, присоединённых к узлу S; при этом со знаком плюс берутся те токи, которые направлены к узлу S, а со знаком минус – в направлении от узла S.
- алгебраическая сумма источников тока, присоединённых к узлу S; при этом со знаком плюс берутся те токи, которые направлены к узлу S, а со знаком минус – в направлении от узла S. =
=  , или
, или 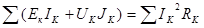 . (4.6)
. (4.6) .
.
 .
.

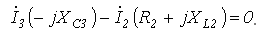






 ,
,  .
. Пример. Составим уравнения методом узловых потенциалов (рисунок 7.3).
Пример. Составим уравнения методом узловых потенциалов (рисунок 7.3). =0.
=0.
 .
. .
.

 ; – к емкостным
; – к емкостным  .
. или
или


 ,
,
 .
.
 и
и  возможны три различных случая.
возможны три различных случая. , а, следовательно,
, а, следовательно,
 , а значит,
, а значит,  . Этот случай отражает векторная диаграмма на рисунке 11.2,б.
. Этот случай отражает векторная диаграмма на рисунке 11.2,б. - случай резонанса напряжений (рисунок 11.2,с).
- случай резонанса напряжений (рисунок 11.2,с). .
.
 .
. .
.

 и
и  должны откладываться от начала координат влево. По оси абсцисс можно откладывать или время t, или пропор-циональную ему угловую величину ωt. Соответственно, периодом будет являться или Т, или 2
должны откладываться от начала координат влево. По оси абсцисс можно откладывать или время t, или пропор-циональную ему угловую величину ωt. Соответственно, периодом будет являться или Т, или 2  .
. называют также углом сдвига тока по отношению к напряжению. При φ=0 ток и напряжение совпадают по фазе, при
называют также углом сдвига тока по отношению к напряжению. При φ=0 ток и напряжение совпадают по фазе, при  - противоположны по фазе, при
- противоположны по фазе, при  - находятся в квадратуре.
- находятся в квадратуре.


