
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика измерений и экспериментальная установкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где
U =αТЭДС.Δ t. (14.11) Порядок выполнения работы Внимание! Нагрев начинается сразу после включения установки в сеть. Заранее подготовьте таблицу для записи опытных данных. 1. Измерьте длину l 0 образца от нижнего конца, упирающегося в головку инди‑ 2. Убедитесь, что индикатор стоит на нуле; милливольтметр также должен показывать нуль. 3. Включите установку в сеть. 4. Когда стрелка милливольтметра отклонится на 10 делений, запишите показания индикатора Δ l. 5. Записывайте удлинение образца Δ l при напряжениях, указанных в табл.14.1. 6. Отключите установку от сети. 7. ВычислитеΔ t по формуле (14.11). 8. Постройте график зависимости Δ l = f (Δ t). 9. По формуле (14.10) определите коэффициент линейного расширения α; сравните полученное значение с табличными; определите, из какого материала сделан образец. 10. Оцените погрешность Δα определения коэффициента линейного теплового расширения. 11. Все полученные результаты занесите в табл.14.1. Таблица 14.1
Контрольные вопросы 1. Как определяется в термодинамике коэффициент линейного расширения твердых тел? 2. Что такое гармоническое приближение? 3. Какие физические свойства нельзя объяснить без учета ангармонизма? 4. Представьте выражение для коэффициента линейного расширения для линейной цепочки атомов в гармоническом приближении и с учетом ангармонического вклада. 5. Как определяется изменение температуры образца в данной работе?
Используемая литература [2] § 43.4; [3] § 5.28.
Лабораторная работа 3-15 Исследование эффекта Зеебека Цель работы: изучение термоэлектрических явлений, измерение температурной зависимости ЭДС термоэлемента.
Теоретическое введение
Если из двух разнородных металлов образовать замкнутую цепь и контакты (спаи) металлов поддерживать при разных температурах, то по цепи пойдёт ток. Это явление получило название термоэлектричества, а возникающая ЭДС – термоэлектродвижущей силы (ТЭДС). Термоэлектри‑ В небольшом диапазоне температур величина ТЭДС
Здесь Величина дифференциальной ТЭДС для пары медь–платина при t =00С равна, например, Термоэлектричество широко используют для измерения температур. Для этого служат термоэлементы (термопары). Они содержат две проволоки из различных металлов, концы которых сварены (спай 1). Второй спай поддерживается при постоянной температуре T 1. Концы цепи присоединяют к милливольтметру. Измерив величину ТЭДС обусловлена зависимостью внутренней контактной разности потенциалов от температуры в спае. Причина появления контактной разности потенциалов между металлами 1 и 2 может быть понята на основе классических представлений об электронном газе в металлах, как об идеальном газе, давление которого определяется числом электронов в единице объема n и температурой Т.
где k – постоянная Больцмана. Так что, если температуры обоих металлов одинаковы, но концентрации разные ( Внутреннюю контактную разность потенциалов
где m – масса молекулы газа, g =9.81 м/с2. В формуле (15.3)
Отсюда получаем
Из (15.5) следует, что чем больше различие в концентрациях электронов, тем больше и внутренняя контактная разность потенциалов. Оценим величину Расхождение устраняется при использовании квантовой теории твёрдого тела. Количественное рассмотрение термоэлектрических эффектов будет иным – необходимо будет ввести понятие энергии Ферми для металлов и пользоваться квантовой статистикой, а не классической.
Экспериментальная часть Приборы и оборудование: термобатарея, термометр, милливольтметр, термопечь.
Методика измерений Экспериментальная установка Схема установки представлена на рис.15.1. Термобатарея 1 представляет собой четыре последовательно соединённые термоэлемента. Термо-ЭДС измеряется милливольтметром 2.
Порядок выполнения работы Внимание! Нагрев начинается сразу после включения установки в сеть. Заранее подготовьте таблицы для записи опытных данных. 1. Запишите в табл.15.1 комнатную температуру t 0. 2. Установите тумблер 8 в нижнее положение. 3. Переключатель 3 установите в положение «4». При этом вольтметр измеряет напряжение на четырёх последовательно соединённых термоэлементах. 4. Включите вилку в розетку; при этом начнётся нагрев. 5. В процессе нагрева через 5 градусов записывайте значения ТЭДС по милливольтметру в табл.15.1. 6. При приближении температуры к 1000С нагрев замедлится. При t= 1000С измерьте ТЭДС при положениях переключателя 3 в положениях «4», «3», «2» и «1». Данные запишите в табл.15.2. 7. Установите снова переключатель 3 в положение «4». 8. Тумблер 8 поставьте в верхнее положение; при этом нагрев ускорится. 9. Продолжите измерения по пункту 5; данные записывайте в табл.15.1.
Таблица 15.1
10. При t= 1750С нагрев снова замедлится; измерьте ТЭДС при этой температуре аналогично пункту 6 при положениях переключателя 3 в положениях «4», «3», «2» и «1». Данные запишите в табл.15.2. 11. Отключите установку от сети.
13. По графику определите удельную ТЭДС: 14. Оцените погрешность Δα. Все результаты запишите в табл.15.1. 15. По данным табл.15.2 рассчитайте удельную ТЭДС одного термоэлемента:
16. По каждой серии опытов рассчитайте среднее значение α1; оцените погрешность Δα1. Таблица 15.2
Контрольные вопросы
1. В чём заключается явление термоэлектричества? 2. Запишите формулу для ТЭДС 3. Дайте определение удельной ТЭДС. 4. Как объясняет классическая электронная теория металлов пропорциональность ТЭДС разности температур спаев двух металлов? 5. Почему классическая электронная теория металлов даёт неверный порядок величины удельной ТЭДС? 6. Где применяются термопары, термобатареи? Используемая литература
[1] § 44.1; [6] § 44; [7] § 247.
Лабораторная работа 3-16
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.81.47 (0.007 с.) |

 Построив график зависимости Δ l = f (Δ t), по тангенсу угла наклона графика к оси ОХ (рис.14.1) можно определить коэффициент линейного расширения α:
Построив график зависимости Δ l = f (Δ t), по тангенсу угла наклона графика к оси ОХ (рис.14.1) можно определить коэффициент линейного расширения α: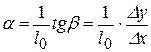 , (14.10)
, (14.10)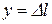 ,
, 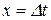 .
.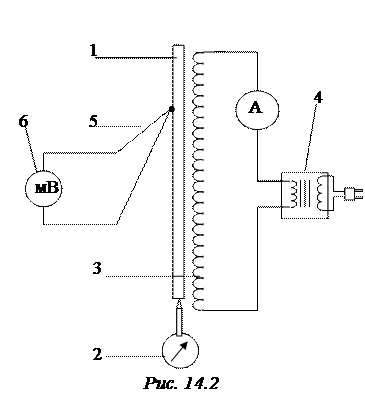 Исследуемый образец (трубка) 1 закреплён верхним концом на станине (рис.14.2). Для измерения удлинения трубки используется индикатор 2. Его измерительная головка упирается в нижний конец трубки. Цена деления индикатора 10-5 м. Внутри трубки находится нагреватель 3 (нихромовая проволока). С понижающего трансформатора 4 на нагреватель подаётся напряжение 20 В. Температура образца измеряется с помощью термопары 5, соединённой с милливольтметром 6. Удельная термо-ЭДС термопары равна αТЭДС=1.43.10-3 В/К (см. лабораторную работу 3-15). Напряжение U, измеряемое милливольтметром, пропорционально разности температур Δ t = t – t 0 двух контактов термопары:
Исследуемый образец (трубка) 1 закреплён верхним концом на станине (рис.14.2). Для измерения удлинения трубки используется индикатор 2. Его измерительная головка упирается в нижний конец трубки. Цена деления индикатора 10-5 м. Внутри трубки находится нагреватель 3 (нихромовая проволока). С понижающего трансформатора 4 на нагреватель подаётся напряжение 20 В. Температура образца измеряется с помощью термопары 5, соединённой с милливольтметром 6. Удельная термо-ЭДС термопары равна αТЭДС=1.43.10-3 В/К (см. лабораторную работу 3-15). Напряжение U, измеряемое милливольтметром, пропорционально разности температур Δ t = t – t 0 двух контактов термопары: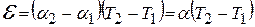 . (15.1)
. (15.1) – коэффициент Зеебека, характеризующий градиент потенциала, который возникает в проводнике, когда его концы поддерживаются при различных температурах. В неравномерно нагретом проводнике в отсутствие тока появляется электрическое поле.
– коэффициент Зеебека, характеризующий градиент потенциала, который возникает в проводнике, когда его концы поддерживаются при различных температурах. В неравномерно нагретом проводнике в отсутствие тока появляется электрическое поле. 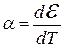 – дифференциальная ТЭДС пары проводников, она зависит не только от рода данной пары проводников, но и от их состояния, в частности, от температуры; T 2 – температура одного из спаев, T 1 – температура другого (T 2 > T 1).
– дифференциальная ТЭДС пары проводников, она зависит не только от рода данной пары проводников, но и от их состояния, в частности, от температуры; T 2 – температура одного из спаев, T 1 – температура другого (T 2 > T 1).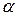 =7.4.10-6 В/К.
=7.4.10-6 В/К. и зная T 1 и
и зная T 1 и 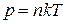 , (15.2)
, (15.2)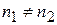 ), то давления электронного газа в этих металлах различны. Если, например,
), то давления электронного газа в этих металлах различны. Если, например,  , то электроны будут переходить из металла 1 в металл 2 в большем количестве, чем из 2 в 1 до тех пор, пока электрическое поле, возникающее вследствие преимущественного диффузионного перехода электронов, не компенсирует своим противодействием влияния перепада давления.
, то электроны будут переходить из металла 1 в металл 2 в большем количестве, чем из 2 в 1 до тех пор, пока электрическое поле, возникающее вследствие преимущественного диффузионного перехода электронов, не компенсирует своим противодействием влияния перепада давления.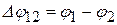 легко оценить в рамках классической электронной теории. Задача о равновесии электронов в двух соприкасающихся проводниках не отличается от задачи о равновесии идеального газа в поле силы тяжести. В соответствии с классической статистикой, концентрация газа
легко оценить в рамках классической электронной теории. Задача о равновесии электронов в двух соприкасающихся проводниках не отличается от задачи о равновесии идеального газа в поле силы тяжести. В соответствии с классической статистикой, концентрация газа 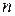 на высоте
на высоте 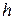 связана с концентрацией
связана с концентрацией  у поверхности Земли распределением Больцмана
у поверхности Земли распределением Больцмана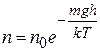 , (15.3)
, (15.3) есть разность потенциальных энергий
есть разность потенциальных энергий  молекулы газа на высоте
молекулы газа на высоте 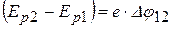 и поэтому
и поэтому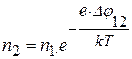 . (15.4)
. (15.4)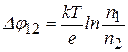 . (15.5)
. (15.5)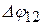 . При комнатной температуре (Т =300 К) величина
. При комнатной температуре (Т =300 К) величина  В, величина же
В, величина же 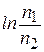 порядка единицы. Поэтому
порядка единицы. Поэтому  Переключатель 3 позволяет измерять напряжение на одном, двух, трёх или четырёх термоэлементах батареи. Термобатарея смонтирована в теплоизолированном корпусе термопечи 4; нагревается с помощью нагревательной спирали 5. Температура измеряется термометром 6. Нагреватель подключается к сети через индуктивное сопротивление 7. Тумблер 8 позволяет включать последовательно с нагревателем печи одно или два индуктивных сопротивления; при этом нагрев ускоряется или замедляется.
Переключатель 3 позволяет измерять напряжение на одном, двух, трёх или четырёх термоэлементах батареи. Термобатарея смонтирована в теплоизолированном корпусе термопечи 4; нагревается с помощью нагревательной спирали 5. Температура измеряется термометром 6. Нагреватель подключается к сети через индуктивное сопротивление 7. Тумблер 8 позволяет включать последовательно с нагревателем печи одно или два индуктивных сопротивления; при этом нагрев ускоряется или замедляется. 12. Вычислите Δ Т = t – t 0, запишите в табл.15.1. Постройте график зависимости
12. Вычислите Δ Т = t – t 0, запишите в табл.15.1. Постройте график зависимости  в соответствии с формулой (15.1).
в соответствии с формулой (15.1).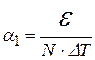 .
.


