
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение опыта Франка и Герца.Содержание книги
Поиск на нашем сайте
Цель работы: изучение дискретного характера энергетического спектра атомов ртути и определение возможных энергетических состояний атома. Теоретическое введение Постулаты Бора В 70-х годах XIX столетия Максвелл в статье для энциклопедии писал: «Атом есть тело, которое нельзя рассечь пополам». В это же время многие факты указывали на органическую связь электронов с атомами: электролиз (1869), катодные и анодные лучи (1886), фотоэффект (1888), рентгеновские лучи (1895). В 1896 году Беккерель обнаружил существование особых лучей, позднее названных радиоактивным излучением, испускаемым соединением урана. Было доказано, что радиоактивное излучение состоит из α-, β-, γ-лучей. В 1903 Резерфорд и Содди утверждали, что это возможно в результате распада атома. Изучение атомных спектров сыграло не последнюю роль в познании строения атомов. Прежде всего, обнаруживается, что в спектрах атомов линии располагаются не беспорядочно, а объединяются в группы, их ещё называют серии линий. Перечисленные выше исследования позволили считать доказанным: внутри атома есть электроны, а силы взаимодействия внутри атомов и молекул - электрического происхождения. Томсон предложил модель атома, согласно которой атом представляет собой равномерно заполненную положительным зарядом сферу, внутри которой находится электрон. Электрон, выведенный из положения равновесия, совершает колебания под действием кулоновских сил. Чтобы выяснить характер распределения положительных и отрицательных зарядов в атоме, необходимо было непосредственное опытное зондирование внутренних областей атома. Такое зондирование было осуществлено в 1911г. Резерфордом с помощью α-частиц (ионизированных атомов гелия 42Не++ ). Он наблюдал изменение направления полёта α -частиц при прохождении их через тонкие слои вещества. Некоторая часть α-частиц отклонялась на углы 135-150º. Это указывало на то, что представление о положительном заряде атома, «размазанном» по объёму, несостоятельно. Анализируя результаты опытов, Резерфорд высказал предположение, что положительные заряды как α-частиц, так и рассеивающего атома сосредоточены в малых объёмах, порядка 10-15 м. Остальная часть атома (размерами ≈10-10 м) представляет собой облако отрицательно заряженных электронов, полный заряд которых равен положительному заряду ядра. В ядерной модели атома электроны не могут быть неподвижны. В результате кулоновских сил притяжения они сразу же упали бы на него. Атому, напротив, свойственна исключительная устойчивость. Устойчивость атома невозможно понять, если ядерную модель объяснять на основе классических законов механики, электричества. Из классической электродинамики следует, что вращающийся электрон должен излучать электромагнитные волны. Теряя свою энергию, электрон должен упасть на протон. Кроме того, по мере приближения к протону линейная и угловая скорости электрона будут увеличиваться. Вследствие этого частота излучения, определяемая частотой обращения электрона вокруг протона, должна была бы непрерывно возрастать. Следовательно, спектр излучения атома должен быть непрерывным, но не линейчатым. Чтобы объяснить наблюдаемую устойчивость атома водорода и его линейчатый спектр, Бор предложил следующие постулаты: Постулат стационарных состояний: 1. Электрон в атоме может находиться только на стационарной орбите; при этом он не излучает и не поглощает энергии. Круговые стационарные орбиты определяются условием квантования момента импульса
Здесь n – номер орбиты, Правило частот: 2. Излучение (или поглощение) энергии атомом происходит только при переходе электрона с одной орбитына другую. При переходе с одной стационарной орбиты на другую электрон излучает (поглощает) квант света с частотой ν и энергией hν, равной разности энергий стационарных состояний, между которыми произошел переход:
Этот постулат отражает закон сохранения энергии и гипотезу Планка-Эйнштейна о квантах. Динамика электрона на стационарной орбите определяется уравнениями классической теории. Неизбежное следствие: так как остальные орбиты для электрона запрещены, переход осуществляется скачком; о пути и энергии электрона между орбитами говорить не имеет смысла: законы механики там не применимы. Опыт Франка и Герца Из этих представлений следует, что поглощение и излучение энергии атомом должно происходить определёнными дозами. Франк и Герц для проверки этих положений исследовали поглощение энергии атомами при их столкновении с электронами.
Определялась зависимость силы тока I в цепи анода (измерявшейся гальванометром Г)от напряжения U. П олученные результаты представлены на рис.9.2. Сила тока вначале монотонно возрастает, достигает максимума при U = 4.9 В, после чего с дальнейшим увеличением U резко падает, достигает минимума и снова начинает расти. Максимумы силы тока повторяются при U, равном 9.8 В, 14.7 Ви т. д. Такой ход кривой объясняется дискретностью энергетических уровней. Электроны, встречающие на своем пути атомы ртути, могут испытывать с ними соударения упругие, в результате которых энергия не изменяется, а изменяется лишь направление скоростей электронов, или неупругие, в результате которых электроны теряют энергию, передавая ее атомам ртути. В соответствии с постулатами Бора, атом ртути не может принять энергию в любом количестве; атом может воспринять лишь определенную порцию энергии и перейти при этом в одно из возбужденных энергетических состояний. Ближайшее к основному состоянию атома ртути отстоит от основного по шкале энергий на 4.86 эВ. До тех пор, пока электроны, ускоряемые полем, не приобретут энергию еU 1=4.86 эВ, они испытывают лишь упругие столкновения и анодный ток возрастает с ростом U. Как только кинетическая энергия электронов достигает значения 4.86 эВ, начинают происходить неупругие столкновения. Электрон с таким значением энергии
полностью отдает ее атому ртути, не сможет преодолеть задерживающее поле и не достигнет анода. Таким образом, при разности потенциалов между катодом и сеткой, равной 4.86 эВ, должно происходить резкое падение анодного тока. Аналогичное явление будет происходить при еU 2=2.4.86 эВ, … еU n= n .4.86 эВ, когда электроны могут испытать 2, 3 и т.д. неупругих столкновения с атомами ртути, потерять всю свою энергию и не достигнуть анода. Опыт Франка и Герца показал, что 4.86 эВ – наименьшая возможная порция энергии (наименьший квант энергии), которая может быть поглощена атомом ртути в основном энергетическом состоянии, что и является проявлением дискретности уровней энергии в атоме. Таким образом, зависимость, приведённая на рис.9.2, подтверждает справедливость первого постулата Бора. Правило частот Бора также экспериментально подтвердилось в опытах Франка и Герца. Ртутные пары, возбужденные электронным ударом, оказались источником ультрафиолетового излучения с длиной волны λ=253.7 нм. Это излучение происходит в тот момент, когда атом ртути из возбужденного состояния с энергией Е 2 возвращается в основное состояние с энергией Е 1, излучая фотон с частотой ν:
Тогда из (9.3) и (9.4) получим:
По известному значению Δ Е = еU 1=4.86 эВ можно вычислить длину волны излучения: λ=255 нм. Этот результат полностью согласуется с экспериментом: λэксп.=254 нм. Экспериментальная часть Приборы и оборудование: объект исследования, блок управления, осциллограф. Экспериментальная установка В отличие от оригинального опыта в настоящей работе имеется несколько особенностей: · вместо паров ртути объект исследования заполнен инертным газом криптоном; · напряжение на сетке изменяется автоматически блоком управления по линейному закону, синхронно с линейно изменяющимся напряжением горизон‑ · сила анодного тока преобразуется в напряжение, которое подаётся на вертикально отклоняющиеся пластины прибора; · блок управления формирует метку, накладываемую на изображение на экране осциллографа. С помощью ручек «грубо» и «точно» метка перемещается в горизонтальном направлении (рис.9.4), а на цифровом индикаторе отображается напряжение между катодом и сеткой.
Порядок выполнения работы
1. В соответствии с рис.9.3 проводится взаимное соединение приборов.
3. На осциллографе переключателем V/дел и mS/дел устанавливаются соответственно в положения 0.2V/дел и 5mS/дел. 4. С разрешения преподавателя сначала включается осциллограф, затем блок управления. 5. Регуляторами «стабильность» и «уровень» добиваются устойчивого изображения на экране. 6. Регуляторами «грубо» и «точно» метка устанавливается против соответствующего пика на экране, а по индикатору считывается напряжение U между катодом и сеткой. Каждое измерение сделать не менее трёх раз; результаты усреднить. Все данные записываются в табл.9.1. 7. Зная длину волны в спектре криптона (табл.9.1), рассчитать потенциал возбуждения U возб,. пользуясь формулой (9.5).
Таблица 9.1
8. Пользуясь полученным значением U возб. и справочными данными табл.9.2 о потенциалах ионизации, найти соответствие измеренных значений напряжения табличным: возбуждения U возб., ионизации или их сочетания (например, 2 U возб. или U возб+ U и1 и т.д.). Рассчитать соответствующую сумму U теор., записать в таблицу 9.1. Таблица 9.2
9. Результаты измерений U и теоретические U теор. сравниваются между собой, и рассчитывается относительная погрешность результатов измерения:
10. По формуле (9.5) рассчитать длину волны λэксп, соответствующую первому измеренному потенциалу, записать в табл.9.1. Рассчитать погрешность, используя справочные данные по длинам волн в спектре криптона:
11. На миллиметровой бумаге по точкам строится изображение с экрана осциллографа. Контрольные вопросы 1. Схема опыта Резерфорда по рассеянию α-частиц. Какие результаты и выводы из них были при этом получены? 2. В чём состояла невозможность классического истолкования ядерной модели атома водорода? 3. Сформулируйте постулаты Бора. 4. Схема опыта Франка и Герца. 5. Каков главный результат опыта Франка и Герца? Какие выводы были сделаны из экспериментальной зависимости рис.9.2? 6. Какими явлениями обусловлено свечение объекта исследования? Используемая литература
[1] §§ 38.1-38.5; [2] § 29.1; [3] §§ 4.2, 4.3; [6] § 21; [7] § 211.
Лабораторная работа 3-10 Изучение поглощения света Цель работы: измерение спектров поглощения, проверка закона Бугера.
Теоретическое введение Из опытов известно, что при прохождении света в веществе его интенсивность уменьшается. Поглощением света называется явление уменьшения энергии световой волны при её распространении в веществе, происходящее вследствие преобразования энергии волны во внутреннюю энергию вещества или в энергию вторичного излучения с другим спектральным составом и направлениями распространения. Поглощение света может вызвать нагревание вещества, возбуждение и ионизацию атомов или молекул, фотохимические реакции и другие процессы в веществе.
Знак «–» указывает на то, что интенсивность уменьшается. Коэффициент пропорциональности
Здесь I 0 и I – интенсивности излучения на входе и на выходе из слоя среды толщиной d. После преобразований получим:
Выражение (10.2) называется законом Бугера. Выясним физический смысл натурального показателя поглощения. Из (10.2) следует, что если толщина слоя Для разбавленного раствора поглощающего вещества в непоглощающем растворителе выполняется закон Бера:
где С – концентрация раствора, а c – коэффициент пропорциональности, не зависящий от концентрации. В концентрированных растворах закон Бера нарушается из-за влияния взаимодействия между близко расположенными молекулами поглощающего вещества. Из (10.2) и (10.3) получаем закон Бугера-Ламберта-Бера:
Отношение
Оптическая плотность определяется натуральным (или десятичным) логарифмом пропускания:
Коэффициент поглощения зависит от длины волны света λ (или частоты ω). У вещества, находящегося в таком состоянии, что атомы или молекулы практически не воздействуют друг на друга (газы и пары металлов при невысоком давлении), коэффициент поглощения для большинства длин волн близок нулю и лишь для очень узких спектральных областей обнаруживает резкие максимумы (на рис.10.2 показан спектр паров натрия). Эти максимумы, согласно элементарной электронной теории Лоренца (см. лабораторную работу 3.05), соответствуют резонансным частотам колебаний электронов в атомах. В случае многоатомных молекул обнаруживаются также частоты, соответствующие колебаниям атомов внутри молекул. Так как массы атомов гораздо больше массы электрона, молекулярные частоты намного меньше атомных – они попадают в инфракрасную область спектра.
Металлы практически непрозрачны для света. Это обусловлено наличием в металлах свободных электронов. Под действием электрического поля световой волны свободные электроны приходят в движение – в металле возникают быстропеременные токи, сопровождающиеся выделением ленц-джоулева тепла. В результате энергия световой волны быстро уменьшается, превращаясь во внутреннюю энергию металла. В рамках элементарной электронной теории Лоренца удалось объяснить сам факт наличия полос поглощения, однако различие в интенсивностях полос в рамках классической теории объяснить не удаётся. В квантовой механике, как и в полуклассической теории Бора, излучение и поглощение квантов света происходит лишь с частотами, удовлетворяющими правилу частот Бора: переход атома из состояния n с энергией E n в состояние m с энергией E m сопровождающийся поглощением или излучением фотона с частотой
описывается с помощью общего уравнения Шредингера. При этом волновая функция электрона в процессе перехода зависит не только от координат, но и от времени: ψ=ψ(x,y,z,t)=C1.ψn+C2.ψm. Здесь ψn и ψm – волновые функции оптического электрона в состояниях n и m, а коэффициенты C1 и C2 зависят от времени. Средняя мощность излучения пропорциональна величине
где r – расстояние оптического электрона до ядра атома. То есть, интенсивность линии в спектре излучения, а также и в спектре поглощения, пропорциональна величине Спектр (набор линий поглощения или испускания атома) однозначно характеризует данный элемент и может использоваться для качественного спектрального анализа. Изучение молекулярных спектров позволяет получить информацию о структуре молекул, межатомных расстояниях, массах атомов, моментах инерции и дипольных моментах молекул. По смещению и уширению полос в конденсированной фазе можно судить о характере и силе межмолекулярных взаимодействий.
Экспериментальная часть Приборы и оборудование: колориметр фотоэлектрический однолучевой КФО; набор образцов.
Экспериментальная установка
Принцип работы колориметра фотоэлектрического однолучевого КФО заключается в измерении отношения двух световых потоков, полного и прошедшего через измеряемую среду, методом пропорциональных отклонений. На фотоприёмник поочерёдно направляются световые потоки: полный Ф0 и пропущенный через измеряемую среду Ф. Коэффициент пропускания τ измеряемой среды, представляющий собой отношение этих потоков, определяется в виде отношения соответствующих фототоков непосредственно по шкале микроамперметра:
где I 0 – фототок, соответствующий полному световому потоку Ф0, I – фототок, соответствующий световому потоку Ф, прошедшему через измеряемую среду.
Фотометрический клин 5, установленный перед фотоприёмником, предназначен для выставления отсчёта 100 по шкале микроамперметра. Внешний вид прибора представлен на рис.10.5. Порядок выполнения работы. Задание 1. Измерение зависимости пропускания, оптической плотности и коэффициента поглощения от длины волны (измерение спектров поглощения)
2. Держатель образцов достаньте из кюветного отделения 2. 3. Ручку «кюветы» установите крайнее левое положение. 4. Установите нуль по верхней шкале микроамперметра ручкой «установка 0» при открытой крышке кюветного отделения (шторка при этом автоматически закроется). 5. Установите в держателе образец №1, вставьте держатель с образцом в кюветное отделение. Убедитесь, что при этом световой поток идёт МИМО образца. 6. Установите ручку «поглотители» в положение «5», при этом на пути светового потока будет установлен светофильтр 5. 7. Закройте крышку кюветного отделения и с помощью ручки «установка 100» выставьте отсчёт «100» по верхней шкале прибора. 8. Введите образец, для чего ручку «кюветы» поставьте в крайнее правое положение (открыв крышку кюветного отделения, можно проверить, что световой поток проходит через образец). 9. При закрытом кюветном отделении измерьте и запишите в табл. 10.1 пропускание образца τ по верхней шкале. 10. Ручку «кюветы» установите снова в крайнее левое положение. 11. Ручкой «поглотители» установите следующий светофильтр (4, 3, 2 или 1) и повторите измерения образца по пунктам 7-10; все данные запишите в табл. 10.1.
Таблица 10.1
12. Установите в держателе образец №2. Повторите измерения τ на светофильтрах 5-1 по пунктам 7-11. 13. Те же измерения (пункты 6-12) повторите для образцов №3 и 4. 14. Измерьте штангенциркулем толщину d образцов. 15. Рассчитайте оптическую плотность и коэффициент поглощения при каждом измерении:
16. Постройте графики зависимостей τ = f (λ) и À= f (λ) для измеренных образцов.
Задание 2. Измерение коэффициента поглощения. Проверка закона Бугера 1. Ручкой «поглотители» установите светофильтр № 3. 2. Установите в держателе образец № 3 (жёлтый). Измерьте пропускание τ (пункты 7-10 первого задания), запишите в табл.10.2. 3. Добавьте в держатель ещё один такой же образец и измерьте пропускание для двойного слоя вещества. 4. Повторите те же измерения для трёх (n =3) и четырёх (n =4) слоев, все результаты запишите в табл.10.2. 5. Микрометром измерьте толщину образца d. 6. Рассчитайте оптическую плотность по (10.10) и коэффициент поглощения
где n – число слоёв измеряемого образца (n =1÷4). 7. Рассчитайте среднее значение Таблица 10.2
8. Установите в держателе образец № 4 (красный). Повторите измерения по пунктам 2-7 второго задания на светофильтре № 5; при смене светофильтра не забудьте выставить «100» (пункт 7 первого задания); все данные занесите в табл.10.2. 9. Сделайте выводы. Контрольные вопросы 1. Выведите закон Бугера. 2. Каков физический смысл коэффициента поглощения À? 3. Сформулируйте закон Бугера-Ламберта-Бера. 4. Что такое оптическая плотность? Коэффициент пропускания? 5. Почему показатель поглощения среды зависит от длины волны? 6. Почему даже тонкий слой металла практически непрозрачен? 7. Как в квантовой механике объясняется интенсивность спектральных полос? 8. Какой характер имеют спектры (сплошные, полосатые, линейчатые) невзаимодействующих атомов? Молекул? Веществ в конденсированной фазе? Почему? 9. Какие задачи позволяет решить спектральный анализ?
Используемая литература [1] § 33.2; [2] § 26.3; [3] § 3.44; [5] § 103; [7] § 187.
Лабораторная работа 3-11
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1894; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.32.115 (0.013 с.) |

 :
: . (n =1, 2, 3,…∞) (9.1)
. (n =1, 2, 3,…∞) (9.1)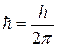 =1.05.10-34Дж.с – постоянная Планка, m – масса электрона, v и r – скорость электрона на орбите соответствующего радиуса. В первом постулате Бора (9.1) прослеживается «насильственное» введение дискретности (разрешены не все орбиты).
=1.05.10-34Дж.с – постоянная Планка, m – масса электрона, v и r – скорость электрона на орбите соответствующего радиуса. В первом постулате Бора (9.1) прослеживается «насильственное» введение дискретности (разрешены не все орбиты).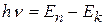 , n>k. (9.2)
, n>k. (9.2)
 (9.3)
(9.3) . (9.4)
. (9.4) . (9.5)
. (9.5)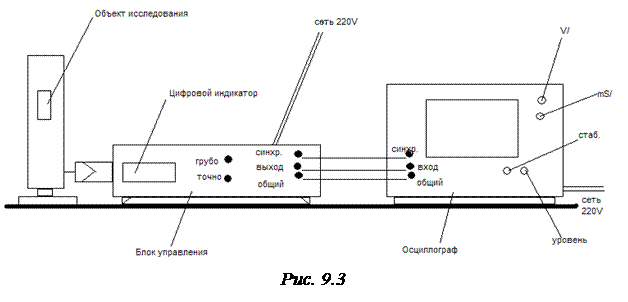
 2. Регуляторы «грубо» и «точно» выводятся против часовой стрелки до упора.
2. Регуляторы «грубо» и «точно» выводятся против часовой стрелки до упора. ,
%
,
%
 ,
%
,
%
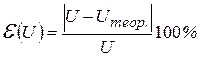
 .
. Ещё в 18 веке Бугер экспериментально, а Ламберт теоретически установили закон поглощения света. При прохождении света через тонкий слой поглощающей среды в направлении x уменьшение интенсивности света dI пропорционально самой интенсивности I и толщине пройденного слоя dx (рис.10.1):
Ещё в 18 веке Бугер экспериментально, а Ламберт теоретически установили закон поглощения света. При прохождении света через тонкий слой поглощающей среды в направлении x уменьшение интенсивности света dI пропорционально самой интенсивности I и толщине пройденного слоя dx (рис.10.1): . (10.1)
. (10.1)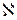 в (10.1) называется натуральным показателем поглощения (коэффициентом поглощения) среды. Он зависит от химической природы и состояния поглощающей среды и от длины волны света. Преобразуем и проинтегрируем это выражение:
в (10.1) называется натуральным показателем поглощения (коэффициентом поглощения) среды. Он зависит от химической природы и состояния поглощающей среды и от длины волны света. Преобразуем и проинтегрируем это выражение: ;
;  ;
; 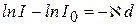 .
. ;
; 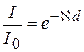 ;
; . (10.2)
. (10.2) , то
, то 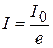 . Таким образом, показатель поглощения равен обратной величине расстояния, при прохождении которого интенсивность света убывает в е≈2.72 раз.
. Таким образом, показатель поглощения равен обратной величине расстояния, при прохождении которого интенсивность света убывает в е≈2.72 раз. , (10.3)
, (10.3) . (10.4)
. (10.4)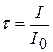 называется коэффициентом пропускания и чаще выражается в процентах:
называется коэффициентом пропускания и чаще выражается в процентах: . (10.5)
. (10.5) . (10.6)
. (10.6)
 Твёрдые тела, жидкости и газы при высоких давлениях дают широкие полосы поглощения (на рис.10.3 представлен спектр раствора фенола). По мере повышения давления газов максимумы поглощения, первоначально очень узкие, всё более расширяются, и при высоких давлениях спектр поглощения газов приближается к спектрам поглощения жидкостей. Этот факт указывает на то, что расширение полос поглощения есть результат взаимодействия атомов (или молекул) друг с другом.
Твёрдые тела, жидкости и газы при высоких давлениях дают широкие полосы поглощения (на рис.10.3 представлен спектр раствора фенола). По мере повышения давления газов максимумы поглощения, первоначально очень узкие, всё более расширяются, и при высоких давлениях спектр поглощения газов приближается к спектрам поглощения жидкостей. Этот факт указывает на то, что расширение полос поглощения есть результат взаимодействия атомов (или молекул) друг с другом.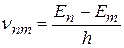 , (10.7)
, (10.7)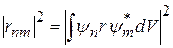 , (10.8)
, (10.8) . Излучение или поглощение света возможно только в том случае, если интеграл в (10.8) отличен от нуля, иначе переход между состояниями n и m оказывается запрещённым. Соответствующие линии в спектрах излучения и поглощения отсутствуют. Так в квантовой механике возникают правила отбора. Например, в спектрах атомов возможны только такие переходы, когда орбитальное квантовое число изменяется на единицу: Δ l =±1, а изменение магнитного квантового числа должно удовлетворять условию Δ ml =0; ±1. Квантовомеханическое рассмотрение дало возможность в согласии с опытом решить задачу не только об отыскании частот спектральных линий атомов, но и об их интенсивностях.
. Излучение или поглощение света возможно только в том случае, если интеграл в (10.8) отличен от нуля, иначе переход между состояниями n и m оказывается запрещённым. Соответствующие линии в спектрах излучения и поглощения отсутствуют. Так в квантовой механике возникают правила отбора. Например, в спектрах атомов возможны только такие переходы, когда орбитальное квантовое число изменяется на единицу: Δ l =±1, а изменение магнитного квантового числа должно удовлетворять условию Δ ml =0; ±1. Квантовомеханическое рассмотрение дало возможность в согласии с опытом решить задачу не только об отыскании частот спектральных линий атомов, но и об их интенсивностях. , (10.9)
, (10.9) Оптическая схема прибора – одноканальная (рис.10.4). Источник света 1 помещён в фокальной плоскости конденсора 3, после которого через измеряемые образцы 8 до фотоприёмника 6 идёт параллельный пучок света. Для выделения отдельных участков спектра используются светофильтры 2 из цветного стекла. Шторка 4 служит для перекрытия светового потока, падающего на фотоприёмник; 7 – защитное стекло кюветной камеры.
Оптическая схема прибора – одноканальная (рис.10.4). Источник света 1 помещён в фокальной плоскости конденсора 3, после которого через измеряемые образцы 8 до фотоприёмника 6 идёт параллельный пучок света. Для выделения отдельных участков спектра используются светофильтры 2 из цветного стекла. Шторка 4 служит для перекрытия светового потока, падающего на фотоприёмник; 7 – защитное стекло кюветной камеры. 1. Включите прибор в сеть, для этого: включите вилку в розетку и включите тумблер на задней стенке прибора.
1. Включите прибор в сеть, для этого: включите вилку в розетку и включите тумблер на задней стенке прибора.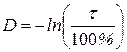 (10.10)
(10.10) . (10.11)
. (10.11)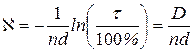 ,
, , запишите в табл.10.2.
, запишите в табл.10.2. , м-1
, м-1
 , м-1
, м-1



