
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента вязкости жидкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
РЕЗУЛЬТАТЫ h = 0.75 м, g =9.8 м/с2 Количество дисков ____
ЛАБОРАТОРНАЯ РАБОТА № 8м ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА
При этом возникают силы, направленные вдоль плоскости соприкосновения и препятствующие их относительному перемещению. Через слои жидкости, прилегающие к плоскостям, они будут воздействовать на них, стремясь затормозить движущуюся Стокс теоретическим путем получил выражение для расчета силы вязкости при движении сферического тела в безграничной среде в случае малых скоростей, при которых не образуется завихрения жидкости, и обтекание тела жидкостью происходит ламинарно:
где Fс - сила вязкости, r - радиус шарика, η - коэффициентвязкости жидкости, υ - скорость движения шарика относительно жидкости. Используя это выражение, можно вычислить вязкость жидкости η, если все остальные величины, входящие в формулу, измерить или вычислить независимым способом. Рассмотрим силы, действующие на шарик, падающий в жидкости (рис. 2). Вертикально вниз действует сила тяготения (
где
где Подставим (1), (3), (4) в (2), получим:
При установившемся движении ускорение шарика
Все величины, входящие в формулу (6), могут быть измерены непосредственно. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Исследуемые жидкости заключены в стеклянные цилиндры, помещенные в кассету. Жидкости подсвечиваются изнутри кассеты люминесцентной лампой. Между лампой и жидкостями установлены экраны из матового стекла, на которых нанесены горизонтальные метки на расстоянии 10 см друг от друга, что позволяет измерить длину пути, пройденного шариком. Измерив время падения шарика между двумя метками (обычно на расстоянии 30 см), можно рассчитать скорость его движения:
где
где d – диаметр шарика. ЗАДАНИЕ. 1. Шарик поместить на предметный столик микроскопа и измерить его диаметр в делениях окулярной шкалы. 2. С помощью стеклянной палочки шарик перенести в исследуемую жидкость и измерить время его падения между двумя выбранными метками. 3. Рассчитать вязкость жидкости по формуле (8). Результаты записать в таблицу. 4. Аналогично провести измерения еще для двух жидкостей, указанных преподавателем. 5. Оценить погрешность измерений, используя следующие формулы:
РЕЗУЛЬТАТЫ g =9.8 м/с2, l =30 см, ρ =7800 кг/м3.
ЛАБОРАТОРНАЯ РАБОТА № 11-Ам РЕЗУЛЬТАТЫ Часть 1.
Часть 2.
Часть 3.
ЛАБОРАТОРНАЯ РАБОТА № 11-Бм РЕЗУЛЬТАТЫ Часть I
Часть II n = 20, Amax =,
ЛАБОРАТОРНАЯ РАБОТА № 12м ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ КРАТКАЯ ТЕОРИЯ. Волнами называются распространяющиеся в упругой среде слабые возмущения. Волны бывают: 1. По природе: а) механические; б) электромагнитные. 2. По характеру колебаний частиц в волне: а) поперечные – волны, в которых направление колебания частиц перпендикулярно направлению распространения волны; б) продольные – волны, в которых направление колебания частиц совпадает с направлением распространения волны. 3. По виду волновой поверхности (под волновой поверхностью понимают геометрическое место точек, колеблющихся в одинаковой фазе): а) плоские; б) сферические. 4. По частоте: а) звуковые (или звук) - волны, частота которых лежит в пределах слышимости человеческого уха (от 20 Гц до 20 кГц). б) инфразвуковые – волны, частота которых меньше 20 Гц. в) ультразвуковые – волны, частота которых больше 20 кГц. Скорость звука u определяется в виде:
где Е – модуль упругости среды,
где R - газовая постоянная ( Важной характеристикой волны является длина волны l - расстояние между двумя ближайшими точками волны, колеблющимися в одинаковой фазе:
где Т – период волны, n= 1/Т - частота колебаний (звука). Математическое выражение, описывающее распространение плоской волны, имеет вид:
где x - отклонение частицы волны в некоторой точке от положения равновесия, А - амплитуда волны,
Источником звука служит электродинамический излучатель 4, подключенный к звуковому генератору. От излучателя 4 в положительном направлении оси х распространяется звуковая волна, описываемая уравнением (4). Волна, дойдя до поршня и отразившись от него, распространяется в обратном нaпpaвлении. При этом в трубе oбpaзуется стоячая волна. Перемещая поршень 2 по трубе 1, находят такое положение Измерив частоту колебаний генератора 5 и длину полуволны, как расстояние
ЗАДАНИЕ 1. На данной частоте в пределах от 1000 Гц до 2000 Гц, заданной преподавателем, установить поршень в положение максимума звука при ближайшем расстоянии 2. Перемещая поршень далее, проделать то же самое для более удаленных положений поршня x 2, x 3, x4 3. Определить среднее значение
и занести в таблицу. 4. Вычислить скорость звука по формуле (5) и записать в таблицу. 5. Повторить измерения еще для двух частот. 6. Провести обработку полученных результатов. Сравнить полученное значение скорости звука с его теоретическим значением. РЕЗУЛЬТАТЫ:
Средний результат: Абсолютная погрешность результата:
Относительная погрешность серии измерений: Окончательный результат:
ЛАБОРАТОРНАЯ РАБОТА № 16м ЛАБОРАТОРНАЯ РАБОТА № 2т ЛАБОРАТОРНАЯ РАБОТА № 7т ОПРЕДЕЛЕНИЕ ВЛАЖНОСТИ ВОЗДУХА И ПОСТОЯННОЙ ПСИХРОМЕТРА АССМАНА КРАТКАЯ ТЕОРИЯ. Влажность воздуха - количество водяных паров в воздухе. Влажность играет существенную роль при протекании многих процессов в метеорологии, сельском хозяйстве, промышленности. От влажности воздуха зависит самочувствие и работоспособность человека. Для количественной характеристики влажности воздуха используют понятия абсолютной и относительной влажности, дефицита влажности. Абсолютная влажность e (кг/м3) - масса водяного пара в единице объема воздуха, т.е. объемная плотность водяного пара в воздухе. Водяной пар является одним из компонентов воздуха. Парциальное давление водяного пара
где Насыщенный пар (н. п.). При данной температуре существует некоторое максимальное значение абсолютной влажности, соответствующее состоянию насыщения пара. Плотность насыщенного пара Е. Тогда:
Отметим, что с ростом температуры максимальное значение абсолютной влажности возрастает. При достижении температуры кипения воды Т=373.15 К (t =100°С) давление воздуха нормальное, давление насыщенного водяного пара При понижении температуры излишки пара конденсируются, превращаясь в туман, росу. Это происходит при температуре При отсутствии центров конденсации возможно перенасыщение пара. Однако такое состояние неустойчиво, т. е. метастабильно. Относительная влажность r (%) равна отношению абсолютной влажности
Дефицит влажности D (кг/м3) - разность между максимальным и наблюдаемым значениями абсолютной влажности:
Измерение влажности воздуха. Приборы для измерения влажности воздуха называют гигрометрами и психрометрами. Точное значение абсолютной влажности определяют, пропуская определенный объем воздуха через трубку, содержащую вещество, поглощающее пары (хлористый кальций, фосфорный ангидрид). Самые простые стрелочные гигрометры содержат нить из обезжиренного человеческого волоса, синтетического материала или органической пленки, которые сокращаются при увеличении влажности, что вызывает поворот стрелки прибора. Такой гигрометр удобен, но имеет большую погрешность измерений. В данной работе для измерения влажности воздуха применяется психрометр Ассмана. Психрометр Ассмана состоит из двух одинаковых жидкостных термометров. Для защиты от теплового излучения окружающих тел их резервуары помещены внутри открытых металлических двустенных трубочек. В верхней части прибора помещен вентилятор, обеспечивающий принудительную циркуляцию воздуха с постоянной скоростью у обоих термометров. Сухой термометр психрометра показывает температуру окружающего воздуха Тепловое равновесие резервуара влажного термометра достигается при равенстве количества теплоты, поступающего от протекающего воздуха, и количества теплоты, необходимого для испарения воды. За одну секунду воздух, обтекающий резервуар, отдает ему количество теплоты, пропорциональное разности температур
где С - коэффициент, зависящий от скорости протекания воздуха. Испаряющаяся вода отнимает за одну секунду у резервуара количество теплоты:
где
Объединяя формулы (6) - (8) при
где На основании психрометрической формулы составляются психрометрические таблицы для вычисления абсолютной и относительной влажности по показаниям сухого и влажного термометров. Постоянная психрометра может быть определена, если известна абсолютная влажность e согласно формуле (9):
ЗАДАНИЕ. 1. Осторожно смочить дистиллированной водой резервуар одного из термометров психрометра, включить вентилятор. При установившемся режиме испарения отсчитать три раза разность температур ( 2. По таблице определить значение плотности насыщенного пара при комнатной температуре. Рассчитать значение плотности водяного пара, используя формулу (3). 3. Определить атмосферное давление и рассчитать постоянную психрометра по формуле (10). РЕЗУЛЬТАТЫ E =, t1 =, р 0 =
r =, D =, A =.
ЛАБОРАТОРНАЯ РАБОТА № 11т МЕТОДОМ КОМПЕНСАЦИИ
Согласно закону Ома для полной цепи:
где e - ЭДС, i - сила тока, r - внутреннее сопротивление источника, U - напряжение на полюсах источника тока. Из формулы (1) видно, что обычные токопроводящие вольтметры непригодны для точного определения ЭДС. При отсутствии тока ЭДС равна напряжению на полюсах источника. Из этого следует, что принципиально возможно измерить ЭДС электростатическим или электронным вольтметром (вольтметрами, не потребляющими тока). Наиболее точным методом измерения ЭДС является метод компенсации. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Принципиальная схема компенсационного метода измерения ЭДС изображена на рис. 1. Вспомогательная батарея
Для того, чтобы исключить из уравнения (2) силу тока, вместо неизвестного элемента переключателем К подключают к цепи нормальный элемент Вестона (рис.1) с известной ЭДС Условие компенсации выразится равенством: Из (2) и (3) имеем: или
ЗАДАНИЕ. 1. Собрать схему (рис. 2) и поставить рукоятку тумблера К1 в такое положение, чтобы был включен элемент 2. Перекинуть рукоятку тумблера К1 и включить элемент
РЕЗУЛЬТАТЫ
ЛАБОРАТОРНАЯ РАБОТА № 6э ИЗУЧЕНИЕ ЗАВИСИМОСТИ МОЩНОСТИ ИСТОЧНИКА ТОКА ОТ СОПРОТИВЛЕНИЯ НАГРУЗКИ КРАТКАЯ ТЕОРИЯ. В электрической цепи, содержащей источник тока с ЭДС e и внутренним сопротивлением r, на резисторе R (рис.1) будет выделяться полезная мощность:
где I - сила тока. Согласно закону Ома для замкнутой цепи:
Из (1) и (2) следует что:
Ток I протекает так же и внутри источника, и поэтому в нем выделяется мощность
Полная мощность источника:
Полезная мощность источника
а затем убывает, стремясь к нулю при
ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ 1. Собрать цепь, состоящую из источника тока, ключа, магазина резисторов R согласно рис.1. 2. Снять зависимость тока I от сопротивления R. Результаты записать в виде таблицы. Изменение R с помощью декадных переключателей магазина производить при разомкнутом ключе. Ключ замыкается только на время проведения измерения. 3. Рассчитать полезную мощность по формуле (1) и вычертить график зависимости Рп (R). 4. По графику определить r, Pпmaх и, используя (6), рассчитать ЭДС источника тока e. ЛАБОРАТОРНАЯ РАБОТА № 13э ЛАБОРАТОРНАЯ РАБОТА № 14э С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА КРАТКАЯ ТЕОРИЯ. Интерференцией волн называется процесс наложения волн, при котором происходит их взаимное усиление или ослабление. Интерферировать могут волны любой природы, в том числе и электромагнитные (в частности световые). Устойчивое чередование интерференционных минимумов и максимумов интенсивности (интерференционная картина) наблюдается в случае соблюдения условий когерентности волн: 1. Совпадение частот источников волн. 2. Постоянство разности фаз интерферирующих волн во времени. 3. Одинаковая поляризация интерферирующих волн. При освещении однородной плоскопараллельной пластинки светом разность хода волн, отраженных от верхней и нижней плоскостей, зависит от углов падения и толщины пластинки. Если на пути отраженных лучей установить собирающую линзу, то устойчивая интерференционная картина будет наблюдаться на экране, расположенном в её фокальной плоскости. Поскольку точки фокальной плоскости линзы сопряжены бесконечно удаленным,то говорят, что интерференционная картина локализована в бесконечности. Отметим, что в данном случае устойчивая интерференционная картина образуется параллельными лучами, отраженными от пластинки. Наблюдаемые на экране полосы названы полосами равного наклона. При освещении пластинки (например, клина) параллельным пучком лучей разность хода лучей, отраженных от верхней и нижней поверхностей пластинки зависит от толщины пластинки. Ввиду непараллельности поверхностей отраженные лучи пересекутся на конечном расстоянии от отражающих плоскостей, и интерференционная картина будет локализована вблизи пластинки. Поскольку в этом случае разность хода определяется лишь толщиной пластинки, то для ее точек, соответствующих одинаковому расстоянию между отражающими поверхностями, условия максимумов и минимумов неизменны. Такие интерференционные полосы называются полосами равной толщины. В данной работе исследуются полосы равной толщины, которые возникают в результате интерференции волн, отраженных от границы прослойки между сферической поверхностью линзы и поверхностью плоской пластинки. Интерференционные полосы, возникающие в этой системе, имеют вид концентрических окружностей (колец). Они называются кольцами Ньютона. При нормальном падении лучей и большом радиусе кривизны поверхности линзы можно пренебречь различием в углах падения лучей на сферическую поверхность. Тогда разность хода волн
По рис. 1 имеем:
Темные кольца (минимум освещенности) образуются при условии:
Из (4) и (5) радиусы темных (rm) и светлых (rc) колец:
Рис. 3 РЕЗУЛЬТАТЫ
ЛАБОРАТОРНАЯ РАБОТА № 4о Преломляющий угол призмы
Учитывая (1), (2), (3), найдем:
Угол выхода лучей
Метод полного отражения. Свет вводится в рефрактометр через матовую грань DF призмы Р2. Свет падает на эту грань под всевозможными углами. При углах падения При освещении призм белым светом граница раздела будет размыта и окрашена в различные цвета из-за дисперсии в призме Р2. Чтобы получить резкое изображение, перед объективом зрительной трубы помещаются две пр
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.106 (0.014 с.) |

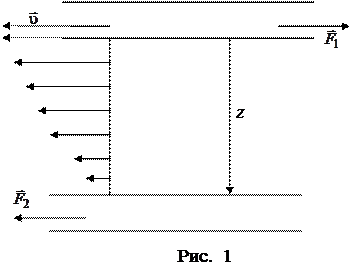 КРАТКАЯ ТЕОРИЯ. Пусть между двумя параллельными плоскостями находится слой жидкости толщиной z. Если одна из плоскостей движется относительно другой со скоростью
КРАТКАЯ ТЕОРИЯ. Пусть между двумя параллельными плоскостями находится слой жидкости толщиной z. Если одна из плоскостей движется относительно другой со скоростью  , то вместе с ней движется и тонкий слой прилипшей к ней жидкости. Такой же слой прилипает и к неподвижной плоскости. Промежуточные слои жидкости движутся со скоростями, убывающими по мере приближения к неподвижной плоскости (рис. 1).
, то вместе с ней движется и тонкий слой прилипшей к ней жидкости. Такой же слой прилипает и к неподвижной плоскости. Промежуточные слои жидкости движутся со скоростями, убывающими по мере приближения к неподвижной плоскости (рис. 1). и сдвинуть с места неподвижную
и сдвинуть с места неподвижную  . Согласно третьему закону Ньютона эти силы равны по абсолютной величине и противоположны по направлению. Силы называются силами вязкости или силами внутреннего трения.
. Согласно третьему закону Ньютона эти силы равны по абсолютной величине и противоположны по направлению. Силы называются силами вязкости или силами внутреннего трения.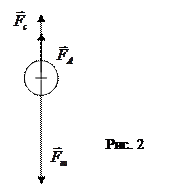
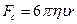 , (1)
, (1) ), которая больше выталкивающей силы Архимеда (
), которая больше выталкивающей силы Архимеда ( ), направленной вверх, т. к. плотность шарика больше плотности жидкости. В начале движения равнодействующая этих двух сил отлична от нуля, шарик будет двигаться ускоренно. Однако сила сопротивления будет увеличиваться, равнодействующая сил уменьшаться и при некоторой скорости станет равной нулю. Начиная с этого момента, шарик будет двигаться равномерно с некоторой установившейся скоростью. Если скорость шарика в результате действия каких-либо случайных факторов изменит свое значение, то это приведет к изменению силы сопротивления движению, кратковременно появится ускорение, и скорость снова примет установившееся значение. II закон Ньютона для шарика, записанный в проекции на направление его движения, имеет следующий вид:
), направленной вверх, т. к. плотность шарика больше плотности жидкости. В начале движения равнодействующая этих двух сил отлична от нуля, шарик будет двигаться ускоренно. Однако сила сопротивления будет увеличиваться, равнодействующая сил уменьшаться и при некоторой скорости станет равной нулю. Начиная с этого момента, шарик будет двигаться равномерно с некоторой установившейся скоростью. Если скорость шарика в результате действия каких-либо случайных факторов изменит свое значение, то это приведет к изменению силы сопротивления движению, кратковременно появится ускорение, и скорость снова примет установившееся значение. II закон Ньютона для шарика, записанный в проекции на направление его движения, имеет следующий вид: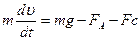 , (2)
, (2) - модульсилы тяжести (3)
- модульсилы тяжести (3) - сила Архимеда, (4)
- сила Архимеда, (4) - плотность жидкости, V – объем шарика,
- плотность жидкости, V – объем шарика,  - плотность материала шарика.
- плотность материала шарика. . (5)
. (5) . Из уравнения (5) найдем значение коэффициента вязкости жидкости:
. Из уравнения (5) найдем значение коэффициента вязкости жидкости: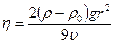 . (6)
. (6) , (7)
, (7) - длина пути, t - время падения шарика. Диаметр шарика определяется с помощью микроскопа или микрометра. Подставив выражение (7) в формулу (6), получим расчетную формулу для вычисления коэффициента вязкости:
- длина пути, t - время падения шарика. Диаметр шарика определяется с помощью микроскопа или микрометра. Подставив выражение (7) в формулу (6), получим расчетную формулу для вычисления коэффициента вязкости: , (8)
, (8) ,
,  ,
,  .
. , Па×с
, Па×с
 , Па×с
, Па×с
 , Па×с
, Па×с
 , Па×с
, Па×с
 Па×с.
Па×с. м/с2.
м/с2. , кг
, кг
 , м
, м
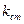 , Н/м
, Н/м
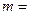
 , с
, с
 , Н/м
, Н/м
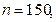
 , см
, см
 , см
, см
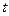 , с
, с
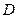

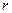 . кг/c
. кг/c
 .
.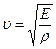 , (1)
, (1) , (2)
, (2) Дж/моль×К), Т – температура воздуха, m - молярная масса (для воздуха μ = 0.029 кг /моль) и g - показатель Пуассона (для воздуха
Дж/моль×К), Т – температура воздуха, m - молярная масса (для воздуха μ = 0.029 кг /моль) и g - показатель Пуассона (для воздуха  ).
). , (3)
, (3) , (4)
, (4) - волновое число, w - циклическая частота колебаний,
- волновое число, w - циклическая частота колебаний,  - расстояние от источника колебаний до данной точки среды.
- расстояние от источника колебаний до данной точки среды.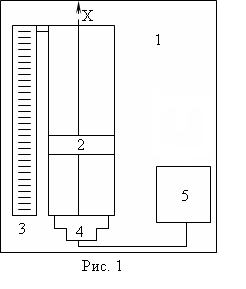 ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Определение скорости звука осуществляется с помощью прибора, состоящего из стеклянной трубки 1 и поршня 2 (рис. 1). Рядом с трубой размещена шкала 3, по которой определяют положение поршня.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Определение скорости звука осуществляется с помощью прибора, состоящего из стеклянной трубки 1 и поршня 2 (рис. 1). Рядом с трубой размещена шкала 3, по которой определяют положение поршня.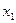 , при котором звук будет максимально сильным. Положение поршня отсчитывают по шкале 3. При смещении поршня от положения
, при котором звук будет максимально сильным. Положение поршня отсчитывают по шкале 3. При смещении поршня от положения  . Поршень перемещается при этом на расстояние, равное половине длины волны:
. Поршень перемещается при этом на расстояние, равное половине длины волны:  .
. (5)
(5) , соответствующих максимумам громкости звука.
, соответствующих максимумам громкости звука. .
. , см
, см
 , см
, см
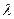 , м
, м
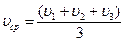 .
. и серии измерений:
и серии измерений: .
. .
. м/с.
м/с.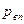 - давление водяного пара в объеме, который занимает весь воздух. Парциальное давление связано с его плотностью
- давление водяного пара в объеме, который занимает весь воздух. Парциальное давление связано с его плотностью  уравнением Менделеева-Клапейрона:
уравнением Менделеева-Клапейрона: , (1)
, (1) - молярная масса водяного пара (
- молярная масса водяного пара (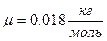 ),
),  - газовая постоянная.
- газовая постоянная. . (2)
. (2) =1 атм. = 1.01×105 Па.
=1 атм. = 1.01×105 Па. , называемой точкой росы, когда плотность водяных паров
, называемой точкой росы, когда плотность водяных паров  .
.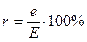 . (3)
. (3) . (4)
. (4)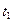 , а влажный – температуру
, а влажный – температуру 
 . Разность температур тем больше, чем меньше относительная влажность воздуха, так как тогда испарение воды происходит быстрее. При
. Разность температур тем больше, чем меньше относительная влажность воздуха, так как тогда испарение воды происходит быстрее. При  (соответствует состоянию насыщения пара) испарение воды у влажного термометра прекращается, и
(соответствует состоянию насыщения пара) испарение воды у влажного термометра прекращается, и  и площади поверхности испарителя S:
и площади поверхности испарителя S: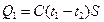 , (6)
, (6) , (7)
, (7) - удельная теплота испарения воды при температуре
- удельная теплота испарения воды при температуре 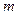 - масса воды, испарившейся за секунду. Эта масса пропорциональна разности между плотностью насыщенного пара
- масса воды, испарившейся за секунду. Эта масса пропорциональна разности между плотностью насыщенного пара 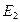 при температуре
при температуре 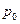 :
: (8)
(8) , получаем соотношение при тепловом равновесии – психрометрическую формулу:
, получаем соотношение при тепловом равновесии – психрометрическую формулу: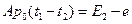 , (9)
, (9)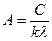 - постоянная психрометра, зависящая от его конструкции и температуры
- постоянная психрометра, зависящая от его конструкции и температуры  . (10)
. (10)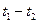 ) и, используя психрометрическую таблицу, определить значение относительной влажности воздуха.
) и, используя психрометрическую таблицу, определить значение относительной влажности воздуха. КРАТКАЯ ТЕОРИЯ. При протекании электрического тока в замкнутой цепи, состоящей из проводника и источника тока (электрической батареи), оказывается, что внутри источника тока положительные заряды должны перемещаться против сил электростатического поля. Это возможно только в том случае, если на заряды действуют силы неэлектрического происхождения, так называемые сторонние силы. Работа сторонних сил по перенесению 1 Кл заряда между теми точками цепи, где они действуют, называется электродвижущей силой (ЭДС):
КРАТКАЯ ТЕОРИЯ. При протекании электрического тока в замкнутой цепи, состоящей из проводника и источника тока (электрической батареи), оказывается, что внутри источника тока положительные заряды должны перемещаться против сил электростатического поля. Это возможно только в том случае, если на заряды действуют силы неэлектрического происхождения, так называемые сторонние силы. Работа сторонних сил по перенесению 1 Кл заряда между теми точками цепи, где они действуют, называется электродвижущей силой (ЭДС):  . ЭДС измеряется в вольтах.
. ЭДС измеряется в вольтах.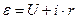 , (1)
, (1) с ЭДС, заведомо превосходящей ЭДС исследуемого элемента, поддерживает ток в цепи реохорда АВ0. Исследуемый источник ЭДС
с ЭДС, заведомо превосходящей ЭДС исследуемого элемента, поддерживает ток в цепи реохорда АВ0. Исследуемый источник ЭДС  одним полюсом присоединен к точке А, а другим - через гальванометр G и сопротивление R к движку реохорда D. Компенсация ЭДС
одним полюсом присоединен к точке А, а другим - через гальванометр G и сопротивление R к движку реохорда D. Компенсация ЭДС  (сопротивлением Rx), чтобы напряжение на нем равнялось
(сопротивлением Rx), чтобы напряжение на нем равнялось  ). В уравновешенной таким образом цепи согласно закону Кирхгофа для контура AD
). В уравновешенной таким образом цепи согласно закону Кирхгофа для контура AD  . (2)
. (2) . Компенсация ЭДС произойдет при новом положении движка (при длине AD равной lN и сопротивления этого участка RN).
. Компенсация ЭДС произойдет при новом положении движка (при длине AD равной lN и сопротивления этого участка RN). . (3)
. (3) (4)
(4) . (5)
. (5) Таким образом, измерение ЭДС сводится к измерению длин участков реохорда. В рассматриваемом методе гальванометр применяется не для измерения тока, а для констатации его отсутствия. Для этих целей применяются приборы, у которых нуль расположен посередине шкалы. Точность измерения ЭДС по схеме на рис. 1 невелика, так как при отсчете длины делаются погрешности более 0,5 мм. Кроме того, в процессе эксплуатации проволока стирается, и ее сопротивление по длине делается неоднородным. Монтажная схема установки изображена на рис. 2. Сопротивление R (порядка 104 Ом) служит для ограничения тока, текущего через гальванометр. Нормальный и исследуемый элемент подключаются к схеме с помощью ключа К2. В опытах батарея
Таким образом, измерение ЭДС сводится к измерению длин участков реохорда. В рассматриваемом методе гальванометр применяется не для измерения тока, а для констатации его отсутствия. Для этих целей применяются приборы, у которых нуль расположен посередине шкалы. Точность измерения ЭДС по схеме на рис. 1 невелика, так как при отсчете длины делаются погрешности более 0,5 мм. Кроме того, в процессе эксплуатации проволока стирается, и ее сопротивление по длине делается неоднородным. Монтажная схема установки изображена на рис. 2. Сопротивление R (порядка 104 Ом) служит для ограничения тока, текущего через гальванометр. Нормальный и исследуемый элемент подключаются к схеме с помощью ключа К2. В опытах батарея 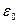 , элементы
, элементы 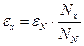 рассчитать ЭДС. Опыты повторить с вторым элементом и обоими элементами, включенными последовательно. Результат представить в виде:
рассчитать ЭДС. Опыты повторить с вторым элементом и обоими элементами, включенными последовательно. Результат представить в виде: .
. , (1)
, (1)
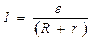 . (2)
. (2) . (3)
. (3) .
. . (4)
. (4) изменяется от нуля при R = 0, проходит через максимум при
изменяется от нуля при R = 0, проходит через максимум при , (5)
, (5) . Максимальное значение полезной мощности:
. Максимальное значение полезной мощности: . (6)
. (6) будет определяться только толщиной зазора:
будет определяться только толщиной зазора: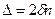 . (1)
. (1) . (2)
. (2)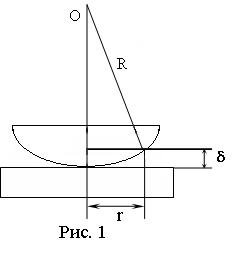 Необходимо учесть, что при отражении от границы раздела стекло-воздух фаза вектора
Необходимо учесть, что при отражении от границы раздела стекло-воздух фаза вектора  не изменяется, в то время как при отражении от границы воздух-стекло происходит потеря половины длины волны, поэтому разность хода интерферирующих лучей в отраженном свете (для n = 1) будет равна:
не изменяется, в то время как при отражении от границы воздух-стекло происходит потеря половины длины волны, поэтому разность хода интерферирующих лучей в отраженном свете (для n = 1) будет равна: . (3)
. (3) (4)
(4) Светлые кольца образуются при условии:
Светлые кольца образуются при условии: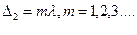

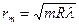 , (6)
, (6)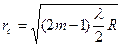 . (7)
. (7) (3)
(3) . (4)
. (4) будет иметь наименьшее значение для скользящих лучей. Лучи, проходящие через грань EF, будут выходить под углами от 90° до
будет иметь наименьшее значение для скользящих лучей. Лучи, проходящие через грань EF, будут выходить под углами от 90° до  На рис. 2 представлен схематически ход лучей в рефрактометре Аббе: 1 - осветительное зеркало, 2 – откидная призма, 3 - основная призма, 4 – матовая грань, 5 - исследуемое вещество, 6 - призмы компенсатора, 7 - объектив трубы, 8 - оборотная призма, 9 - окуляр с отсчетной шкалой, расположенный в фокальной плоскости окуляра. Граница рассматривается через вторую линзу, которая совместно с О1 образует зрительную трубу, установленную на бесконечность. С помощью такой трубы определяется угол
На рис. 2 представлен схематически ход лучей в рефрактометре Аббе: 1 - осветительное зеркало, 2 – откидная призма, 3 - основная призма, 4 – матовая грань, 5 - исследуемое вещество, 6 - призмы компенсатора, 7 - объектив трубы, 8 - оборотная призма, 9 - окуляр с отсчетной шкалой, расположенный в фокальной плоскости окуляра. Граница рассматривается через вторую линзу, которая совместно с О1 образует зрительную трубу, установленную на бесконечность. С помощью такой трубы определяется угол  и
и  рассчитывается показатель преломления.
рассчитывается показатель преломления. будет наблюдаться полное отражение. Лучи, проходящие через грань EF и имеющие угол выхода
будет наблюдаться полное отражение. Лучи, проходящие через грань EF и имеющие угол выхода 


