
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента вязкости жидкости методомСодержание книги
Похожие статьи вашей тематики
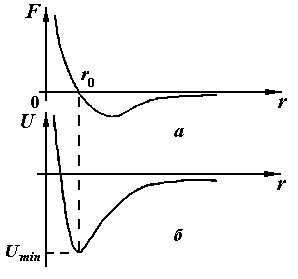
Поиск на нашем сайте Стокса Основные понятия и закономерности Молекулы любого вещества представляют собой устойчивые и трудно деформируемые электрические системы. Эта устойчивость обусловлена тем, что состояние молекул не может меняться непрерывно. Переход молекулы (атома) из одного возможного состояния в другое связан со значительным изменением ее энергии, что и приводит к большей устойчивости. В молекулах суммы положительных и отрицательных зарядов равны, поэтому молекула электрически нейтральна, и электрическое поле за пределами молекул очень быстро убывает с расстоянием. При сближении двух молекул, пока расстояние между их центрами r велико по сравнению с диаметрами молекул d (диаметрами электронной оболочки), силы взаимодействия между молекулами пренебрежительно малы. (рисунок 7.5 а). При дальнейшем сближении двух молекул на расстояниях порядка двух-трех диаметров начинает постепенно проявляться взаимодействие электрических зарядов ядер и электронных оболочек молекул. Благодаря притяжению разноименных и отталкиванию одноименных зарядов произойдет небольшая деформация обеих взаимодействующих молекул, так что распределение зарядов в молекуле станет примерно таким, как показано на рисунке 7.5 б. В результате между молекулами возникнут силы притяжения Fприт. По мере дальнейшего сближения молекул деформация молекул и величина сил притяжения Fприт . будут возрастать. Но когда молекулы подойдут «вплотную» друг к другу и «соприкоснуться» своими электронными оболочками, то дальнейшая деформация молекул будет затруднена. Так как возникнут огромные силы отталкивания Fотт., резко возрастающие при сближении и взаимной деформации молекул (рисунок 7.6 в). Абсолютная величина сил взаимодействия зависит от конкретного строения рассматриваемых взаимодействующих молекул.
На рисунке 7.6 (а, б) изображена примерная зависимость молекулярных сил взаимодействия F от расстояния между молекулами и потенциальной энергии. Значения F < 0 соответствуют силам притяжения, значения F > 0 – силам отталкивания.
На некотором расстоянии ro, характерном для данной пары молекул, притяжение и отталкивание уравновешивают друг друга и результирующая сила взаимодействия становится равной нулю F (ro) = 0. Это расстояние ro соответствует положению равновесия, в котором могут находиться взаимодействующие молекулы при отсутствии теплового движения. Потенциальная энергия взаимодействия молекул в этом состоянии минимальна (рисунок 7.6 б). Так как средняя кинетическая энергия теплового движения молекул пропорциональна КТ, то структура любой совокупности молекул и агрегатное состояние вещества будут существенно зависеть от соотношения величин ï Uмин. ï и КТ. 1) В предельном случае низких температур, когда КТ << ï Uмин .ï, молекулы притянутся друг к другу и расположатся вплотную в определенном порядке – вещество будет находиться в твердом состоянии. Тепловое движение молекул в твердом теле будет в виде малых колебаний около определенных положений равновесия в пространстве. 2) При высоких температурах КТ >> ï Uмин .ï интенсивное тепловое движение молекул будет препятствовать соединению молекул. Вещество при этом будет находиться в газообразном агрегатном состоянии. 3) При промежуточных состояниях, когда КТ» ï Uмин .ï, благодаря тепловому движению, молекулы будут непрерывно перемещаться в пространстве, обмениваясь местами, но не отходя от соседей на расстояние, заметно превышая ro. Вещество при этом будет находиться в жидком агрегатном состоянии. Любое вещество в зависимости от своей температуры может находиться в твердом, жидком или газообразном состоянии. Характер теплового движения молекул жидкости отличается от теплового движения молекул газа. Так как среднее расстояние r между молекулами в жидкости близко ro, то молекулы большую часть времени колеблются около своих положений равновесия. Из-за хаотичности теплового движения скорости и амплитуды колебаний соседних молекул различны, и время от времени соседние молекулы расходятся друг от друга настолько, что отдельные молекулы перескакивают на расстояние порядка d (диаметра молекулы), «застревают» в новых положениях равновесия и начинают колебаться около них. С ростом температуры растет средняя энергия теплового движения, амплитуда колебаний и частота перехода молекул из одного положения равновесия в соседнее. Поэтому в отличие от газа «длина свободного пробега» молекул жидкости имеет порядок диаметра молекул и практически не зависит от внешнего давления и температуры. При практических и теоретических расчетах часто используют кинематический коэффициент вязкости g – отношение динамического коэффициента вязкости к плотности вещества при той же температуре:
Формулу (7.26) можно вывести, используя основные положения молекулярно-кинетической теории.
Перенос количества движения (импульса) между слоями жидкости, движущимися с различными скоростями, подчиняется как и в газах, закону Ньютона:
где S – площадь соприкасающихся слоев;
h – динамический коэффициент вязкости (внутреннего трения), который численно равен силе, действующей между слоями жидкости, имеющими площадь соприкосновения 1 м2 и градиент скорости 1с – 1. Единицей вязкости в СИ является Паскаль×секунда – вязкость, при которой градиент скорости, равный 1м/c на 1 м, приводит к возникновению силы внутреннего трения в 1Н на 1 м2 поверхности соприкосновения слоев. Механизм вязкости жидкости отличен от механизма вязкости газов. Торможение слоев жидкости обусловлено двумя причинами: 1) переносом молекулами импульса при их переходе из слоя в слой в результате теплового движения молекул; 2) наличием сил притяжения между молекулами мономолекулярных слоев (рисунок 7.8). Для того, чтобы сместить первый слой 1 относительно второго 2, необходимо преодолеть силы притяжения между молекулами f (рисунок 7.8). Силы, препятствующие этому смещению слоев, являются силами трения. В жидкостях расстояние между молекулами сравнимо с размерами самих молекул, поэтому силы притяжения между ними велики. И вследствие этого вторая причина, обуславливающая вязкость жидкости, превалирует над первой.
При нагревании жидкости возрастает ее свободный объем (V – b), где b – постоянная в уравнении Ван-дер-Ваальса. Учитывая это, А.И. Бачинский (1877 – 1944) предложил простую формулу, описывающую зависимость жидкости от температуры:
где В – константа, различная для разных жидкостей. Формула Бачинского хорошо оправдывается на опыте, но не показывает явной зависимости коэффициента вязкости от температуры. Я.И. Френкель вывел формулу, связывающую коэффициент вязкости жидкости с температурой:
где w – энергия, которую необходимо сообщить молекуле, чтобы она перешла из одного положения равновесия в другое. Величина w обычно имеет порядок (2-3) 10 – 20 Дж. Поэтому при нагревании жидкости на 100 вязкость ее падает на 20 ¸ 30%. Вязкость жидкости во много раз больше вязкости газа. С ростом температуры вязкость жидкости быстро падает, а вязкость пара медленно возрастает, и при критической температуре Тк они сравниваются друг с другом, как показано на рисунке 7.9.
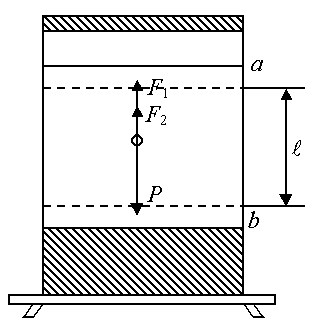
Краткая теория метода Динамический коэффициент вязкости жидкости может быть определен методом падающего шарика в вязкой среде, предложенным Стоксом Рассмотрим падение шарика в вязкой покоящейся жидкости (рисунок 7.10).
На шарик, падающий в этой жидкости, действуют силы: 1. Сила тяжести: P = m g = где r – радиус шарика;
r – плотность вещества, из которого изготовлен шарик, g – ускорение свободного падения. 2. Выталкивающая сила (по закону Архимеда):
где rж – плотность жидкости. Закон Архимеда: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу жидкости, вытесненной данным телом, направленная вертикально вверх. 3. Сила сопротивления движению, обусловленная силами внутреннего трения между слоями жидкости (формула Стокса): F2 = 6p h ru, (7.32) где u – скорость относительного движения слоев жидкости, она равна скорости шарика; h – динамический коэффициент вязкости жидкости. В данном случае играет роль не трение шарика о жидкость, а трение слоев жидкости друг о друга, т.к. при соприкосновении твердого тела с жидкостью к поверхности тела тотчас же прилипают молекулы жидкости. Слой жидкости, непосредственно прилегающий к телу, движется вместе с телом со скоростью движения тела. Этот слой увлекает в своем движении соседние слои жидкости. Для описания движения шарика воспользуемся вторым законом Ньютона:
или в проекциях на направление движения: ma = P – F1 – F2. (7.34) Cначала шарик движется неравномерно, но, начиная с некоторого момента времени, его движение становится равномерным, т.е. а = 0, и уравнение движения примет вид: P – F1 – F2 = 0. (7.35) Подставив значение сил, получим:
Из уравнения (7.36) получим рабочую формулу для опытного определения динамического коэффициента вязкости жидкости:
где u = l/t – скорость шарика в жидкости. Порядок выполнения работы Для нахождения динамического коэффициента вязкости опытным путем необходимо: 1) измерить с помощью микрометра диаметр шарика d; 2) определить плотность вещества шарика или взять ее из таблицы; 3) вычислить скорость падения шарика, для чего следует измерить расстояние между двумя метками на цилиндре l (в этой области шарик движется равномерно) и с помощью секундомера определить время t прохождения шарика между ними; u = l/t. 4) значение плотности жидкости указано на приборе; 5) вычислить по формуле (7.37) значение динамического коэффициента вязкости. Проделать опыт с тремя шариками. Результаты измерения занести в таблицу 7.2
Таблица 7.2
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.011 с.) |


 Þ 1 м2/c. (7.26)
Þ 1 м2/c. (7.26) и
и  – скорости направленного движения слоев 1 и 2 жидкости,
– скорости направленного движения слоев 1 и 2 жидкости,  и
и 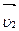 скорости теплового движения молекул, mo – масса одной молекулы. Градиент скорости равен
скорости теплового движения молекул, mo – масса одной молекулы. Градиент скорости равен 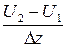 , характеризует изменение скорости направленного движения слоев жидкости (газа) при расстоянии между ними 1 м, измеряется в
, характеризует изменение скорости направленного движения слоев жидкости (газа) при расстоянии между ними 1 м, измеряется в  . Направлен градиент скорости в направлении увеличения скорости.
. Направлен градиент скорости в направлении увеличения скорости.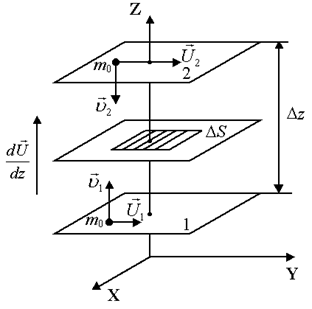
 , (7.27)
, (7.27)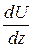 – градиент скорости движения жидкости;
– градиент скорости движения жидкости;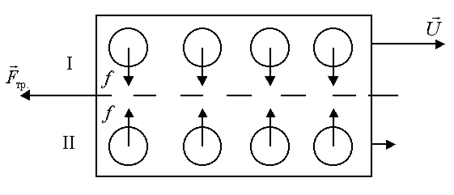

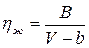 (7.28)
(7.28) (7.29)
(7.29)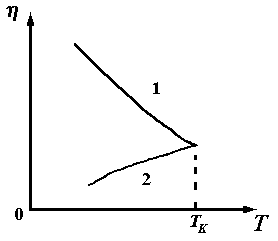
 p r3r g, (7.30)
p r3r g, (7.30)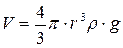 – объем шарика,
– объем шарика, , (7.31)
, (7.31) , (7.33)
, (7.33)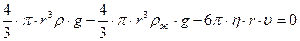 . (7.36)
. (7.36)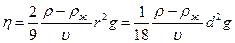 , (7.37)
, (7.37)


