
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Институт электронных и информационных системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЯРОСЛАВА МУДРОГО ИНСТИТУТ ЭЛЕКТРОННЫХ И ИНФОРМАЦИОННЫХ СИСТЕМ СБОРНИК ЛАБОРАТОРНЫХ РАБОТ ПО ОБЩЕМУ КУРСУ ФИЗИКИ Часть I Великий Новгород УДК Печатается по решению РИСа НовГУ
Рецензент А.И. Георгиев, канд. ф.-м. н., доцент каф. ПТиР
СБОРНИК ЛАБОРАТОРНЫХ РАБОТ ПО ОБЩЕМУ КУРСУ ФИЗИКИ. ЧАСТЬ 1 / Сост. Е.А. Ариас, З.С. Бондарева, Ф.А. Груздев, Г.Е. Коровина, А.О. Окунев, Н.А. Петрова. – Великий Новгород: Издательство НовГУ, 2003. – 104 с.
В сборнике приведены описания лабораторных работ по курсу общей физики, включающие разделы «Механика», «Молекулярная физика и термодинамика», «Электростатика» и «Постоянный ток». В каждом описании рассматриваются основные понятия и закономерности, методика и порядок выполнения работы, контрольные вопросы. Настоящий сборник предназначен для студентов института сельского хозяйства, изучающих курс общей физики в течение двух семестров всех форм обучения.
©Новгородский государственный университет, 2003
© Е.А. Ариас З.С. Бондарева, Ф.А. Груздев, Г.Е. Коровина, А.О. Окунев, Н.А. Петрова, составление, 2003.
Содержание
Предисловие 4 1 Лабораторная работа. Измерение физических величин и классификация их погрешностей 5 2 Лабораторная работа. Исследование законов вращательного движения 20 3 Лабораторная работа. Определение момента инерции различных тел методом крутильных колебаний 30 4 Лабораторная работа. Изучение соударения шаров 41 5 Лабораторная работа. Определение ускорения свободного падения при помощи маятника 50 6 Лабораторная работа. Определение отношения теплоемкостей газов по методу Клемана и Дезорма 56 7 Лабораторная работа. Определение коэффициента вязкости жидкости с помощью капиллярного вискозиметра и методом Стокса 66 8 Лабораторная работа. Определение емкости конденсаторов 83 9 Лабораторная работа. Исследование электрической цепи постоянного тока 91 10 Лабораторная работа. Измерение сопротивлений проводников методом мостиковой схемы 95 Библиографический список 103
Предисловие
В настоящий сборник вошли лабораторные работы по курсу общей физики, включающие разделы «Механика», «Молекулярная физика и термодинамика», «Электростатика» и «Постоянный ток». В данный сборник включена лабораторная работа «Измерение величин прямого и косвенного измерений и вычисление их погрешностей (абсолютной и относительной)», что поможет студентам в вычислении погрешностей при выполнении лабораторных работ. Описание каждой лабораторной работы имеет краткое изложение теории физического явления, описание экспериментальной установки, методические указания по выполнению работы и контрольные вопросы. Необходимость теоретического введения к каждой работе основана на том, что студент выполняет лабораторную работу иногда раньше, чем соответствующий материал изложен в лекционном курсе. Контрольные вопросы в каждой работе предназначены для того, чтобы облегчить студентам самоконтроль при изучении материала, обратить их внимание на главное в изучаемом явлении. Все формулы, используемые в данном методическом пособии, выводятся и записываются в Международной системе единиц (СИ). В конце сборника лабораторных работ приводится список рекомендуемой литературы. Настоящий сборник предназначен для студентов института сельского хозяйства, изучающих курс общей физики в течение двух семестров всех форм обучения.
Погрешность измерений
1.2.1 Типы погрешностей
Погрешность результата наблюдения (измерения) есть отклонение результата наблюдения (измерения) Хфизической величины от ее истинного значения Хо. Абсолютная погрешность DХ = Х – Хо выражается в единицах измеряемой физической величины. Относительная погрешность e = DХ/Х выражается в долях или процентах от значения измеряемой физической величины. Очевидно, достоверность результата произведенных измерений будет тем больше, чем меньше погрешность измерений. Результат измерения некоторой физической величины следует записать в виде: Х = (Хо ± DХ) ед.изм. (1.1) Различают три типа погрешностей: 1. Систематическая погрешность При повторении одинаковых наблюдений эта погрешность остается постоянной или изменяется закономерным образом. Если природа и значение таких погрешностей известны, то они могут быть исключены из конечного результата. Устранить систематические погрешности путем повторения опытов нельзя. К систематическим погрешностям можно отнести погрешность измерительного прибора, у которого указан класс точности. 2. Случайная погрешность Она проявляется в хаотическом (случайном) изменении результатов повторных наблюдений. Эти результаты отличаются один от другого и от истинного значения вследствие беспорядочных воздействий большого числа случайных факторов. 3. Промах Эта погрешность возникает в результате небрежности или ослабления внимания экспериментатора. Промахи должны быть исключены из результатов наблюдений. Их легко выявить, поскольку соответствующие результаты заметно отличаются от остальных. При измерениях необходимо учитывать следующее. Если систематическая погрешность заметно превышает случайную, измерение достаточно проводить один раз. В случае, когда превалируют случайные погрешности, измерение необходимо проводить столько раз, чтобы после статистической обработки результатов наблюдений случайная погрешность была меньше систематической ошибки.
1.2.2 Погрешность прямых измерений
При обработке результатов измерений, когда имеется N независимых повторных наблюдений физической величины Хi,где i = 1,2,3 …, N, используют, в основном, два метода вычисления погрешностей: 1) метод расчета среднеквадратичной погрешности, 2) метод расчета средней абсолютной погрешности. Первый метод наиболее точно определяет интервал, внутри которого заключено истинное значение измеряемой физической величины. Второй метод является более простым по сравнению с первым и требует меньшего количества измерений. В данной лабораторной работе рассмотрим расчет среднего арифметического значения физической величины (математического ожидания). Для этого необходимо убедиться, что измерительные приборы не вносят заметных систематических погрешностей в результате измерений и все ошибки измерений можно считать случайными. Пусть в результате наблюдений получено N различных значений измеряемой величины: Хi, X2, X3,…XN.При обработке полученных результатов необходимо определить наиболее вероятное значение измеряемой величины, определить погрешность измерений. В данном случае, в качестве наиболее вероятного значения измеренной величины можно взять среднеарифметическое значение.
Абсолютная погрешность отдельного измерения берется по модулю, так как отклонения результатов наблюдений от наиболее вероятного могут быть как отрицательными, так и положительными:
За погрешность измеренной величины в данном случае принимают среднюю абсолютную погрешность:
В таком случае, запись окончательного результата должна иметь вид:
Приборная погрешность
В ряде случаев многократное проведение наблюдений дает одно и то же значение измеряемой величины. Например, при измерении диаметра цилиндра миллиметровой линейкой получается одно и то же значение d = 45,0 мм. Это не означает, что отсутствует погрешность измерений. Любой измерительный прибор обладает собственной или приборной погрешностью, которая определяется точностью изготовления и градуировки прибора, условиями работы. Приборная погрешность заносится в паспорт прибора. Если специальных указаний нет, то, как правило, в качестве приборной погрешности берется половина наименьшего деления шкалы. В нашем примере величину цилиндра можно записать: d = (45,0 ± 0,5) мм. Если прибор имеет одну шкалу или один предел измерения, тогда наименьшее деление шкалы определяет цену деления прибора. В многопредельных, универсальных приборах шкала обычно не градуируется в значениях измеряемой величины. В таком случае, цена деления прибора зависит от выбранного предела измерения. Предел измерения – это максимально возможная, в данном случае, измеряемая прибором физическая величина. Рассмотрим пример. Предел измерения для вольтметра составляет Umax = 50 B, шкала прибора имеет nmax = 100 делений. Цена деления шкалы:
Стрелка прибора остановилась на nX = 30 дел. Измеренное напряжение в этом случае равно:
Таким образом, для определения значения измеряемой многопредельным прибором физической величины необходимо прежде всего, исходя из выбранного предела измерения
Затем определить искомое значение, умножив показания прибора на цену деления:
Точность прибора определяется точностью его изготовления и градуировки. Согласно ГОСТ все электроизмерительные приборы разделяют на 8 классов точности: 4,0 – 2,5 – 1,5 – 1,0 – 0,5 – 0,2- 0,1 – 0,05. По классу точности можно определить абсолютную погрешность измерительного прибора. Абсолютная погрешность зависит от предела измерения и постоянна в любой части шкалы. Для определения абсолютной погрешности необходимо величину выбранного предела измерения умножить на класс точности. Класс точности задан в процентах. Например, для прибора с классом точности 0,5 при измерении тока на пределе 10А абсолютная погрешность составляет:
Если измерить этим прибором следующие токи
Однако, относительные погрешности, характеризующие качество измерения, будут различны:
Относительная погрешность тем меньше, чем ближе измеряемая величина к пределу измерения. Поэтому рекомендуется выбирать предел таким образом, чтобы измеряемое значение находилось во второй половине шкалы прибора. При использовании стрелочных лабораторных приборов с зеркальной шкалой при считывании показаний необходимо совместить стрелку с ее зеркальным изображением. При таком положении глаза оказывается наименьшей ошибка на параллакс. В случае измерения физических величин сложными приборами и устройствами, приборная погрешность определяется по зависимостям, которые указаны в паспорте прибора. Например, при измерении тока, напряжения, сопротивления универсальными цифровыми приборами относительная погрешность измерения определяется формулами: e e Коэффициенты 0,1 и 0,05 определяются условиями измерения и конструктивными особенностями приборов. X K – конечное значение установленного предела измерений (предел), Х – показания прибора. Выбор формулы (1.8) или (1.9) определяется измеряемой величиной и пределом измерения. Во всех случаях необходимо, для расчета погрешности измерений такими приборами, обращаться к паспортным данным измерительного устройства.
1.2.4. Погрешность единичного измерения
В случае, когда проводится только одно измерение, в качестве его погрешности следует брать приборную погрешность. Например, при измерении микрометром толщины проволоки d = 0,15мм погрешность составит половину цены деления прибора
1.2.5 Погрешность табличных величин
Часто при определении результатов измерения необходимо привлекать табличные (справочные) величины. За погрешность табличной величины принимают единицу в цифре последнего разряда этой величины. Например, табличное значение удельного сопротивления алюминия при 0°С составляет r табл. = 2,53 ×10 – 8 Ом×м. С учетом погрешности табличной величины можно записать
Погрешность табличной величины определяется точностью, с которой необходимо использовать справочные данные. Например, для числа p в различных случаях можно записать:
При записи погрешности, как правило, сохраняется одна значащая цифра.
Содержание отчета
Отчет должен содержать цель работы, перечень используемых приборов с указанием приборной погрешности, таблицы с результатами наблюдений и расчетов. Графики зависимостей одних физических величин от других должны быть построены в строгом соответствии с требованиями пункта 1.5 на миллиметровой бумаге. На графиках необходимо указать погрешности измерений. В заключение отчета необходимо провести краткий анализ результатов.
1.8 Контрольные вопросы
1. Классификация погрешностей. 2. Вычисление погрешностей при прямых измерениях. 3. Приборная погрешность. Класс точности прибора. 4. Как оценивается погрешность измерения при наличии систематических погрешностей и промахов? 5. Округление результатов, погрешность табличной величины. 6. Построение графиков, таблиц, указание погрешностей на графиках. 7. Методы и средства измерения линейных размеров. 8. Определение цены деления основной шкалы и нониуса. 9. Что называют плотностью вещества и в каких единицах она измеряется?
Техника безопасности
1. При работе с микрометром и штангенциркулем измеряемые предметы держать над столом.
Основные понятия и закономерности
Вращательным движением тела называется такое движение, при котором все точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. При вращательном движении тела изменение его кинематических и динамических характеристик зависит от вращающего момента, действующего на тело, и момента инерции тела. Основными кинематическими характеристиками вращательного движения являются угловая скорость ω и угловое ускорение ε:
где φ – угловое перемещение тела или угол поворота. Связь между линейной υ и угловой ω скоростями вращающегося тела и линейным аτ и угловым ε ускорениями можно установить, если выразить длину дуги окружности, по которой происходит вращение, через угол поворота φ: S= φ·r
Тогда:
где r – расстояние от точки до оси вращения (модуль радиуса – вектора точки). Угловая скорость ω и угловое ускорение ε – векторные величины. Вектор Направление вектора При вращательном движении тела изменение его кинематических и динамических характеристик от момента инерции тела и действующего на тело вращающего момента.
Вращающим моментом или моментом вращающей силы называется векторная величина
где Модуль момента силы равен
где r sinα = l – плечо силы F (рисунок 2.2,б) l =OC= r sinα – кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила Твердое тело представляет собой совокупность материальных точек массой mi. Момент сил, действующих на материальную точку, равен
где
Момент сил, действующих на материальные точки:
По второму закону Ньютона
следовательно,
где Соотношение (2.7) можно записать в виде:
где Поэтому момент внешних сил, действующих на тело, – вращающий момент
Следовательно, учитывая соотношения (2.9) и (2.11), имеем
где
Момент внешних сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение
Полученное соотношение (2.13) – основной закон динамики вращательного движения. Из закона динамики вращательного движения следует, что момент силы Для тела плотностью ρ момент инерции вычисляется суммированием моментов инерции всех его материальных точек:
где Момент инерции является физической величиной, характеризующей инертность тела при вращательном движении под действием вращающего момента (аналогично массе тела при поступательном движении, но m = const). Момент инерции тела зависит от формы тела, его размеров и расположения тела относительно оси вращения. Момент инерции тела относительно произвольной оси вращения определяется по теореме Штейнера. Момент инерции тела I относительно произвольной оси вращения ОО равен сумме момента инерции тела I0 относительно оси О/О/, проходящей через центр массы тела параллельно оси ОО, и произведения массы тела m на квадрат расстояния d между параллельными осями (рисунок 2.4).
Порядок выполнения работы
2.3.1 Определение момента инерции ненагруженного маятника
1. Освободить крестовину от грузов. 2. Записать все данные установки: диаметр шкива D, длину стержней l, массу движущегося груза m массу грузов, закрепляемых на стержнях mо. 3. Намотать на шкив нить и подвесить к ней груз массой m, установив его против нулевого деления шкалы. 4. Измерить расстояние h1 от нулевого деления шкалы до нижнего положения груза m по шкале (положение С, рисунок 2.5). 5. Предоставив грузу возможность падать, включить секундомер в момент начала движения груза от нулевого деления и выключить его в момент спуска груза на всю длину нити. Повторить измерения не менее трех раз. Записать значение t и h1 в таблицу 2.1. 6. Измерить высоту h2 максимального подъема груза не менее трех раз. 7. Вычислить: линейное ускорение а, угловое ускорение ε, момент сил трения Мтр ., вращающий момент М и момент инерции I. 8. Все измерения и вычисления записать в таблицу 2.1. 9. Сравнить значение момента инерции ненагруженного маятника, вычисленного по формуле (2.29), с теоретичеcким значением Iкр . формула (2.31). 10. Вычислить абсолютную и относительную погрешности измерений.
2.3.2 Измерение момента инерции маятника с грузами
2. На концах стержней маятника укрепить грузы m0 на расстоянии R от оси вращения. Записать значение R. 3. Грузы необходимо тщательно сбалансировать, чтобы маятник не мог поворачиваться за счет их неточного крепления. 4. Оставляя неизменным падающий груз, можно считать, что момент силы не изменяется, так как в формуле (2.23) ускорение а мало по сравнению с g. 5. Проделать опыт в прежнем порядке, записать среднее время движения груза с высоты h1. 6. Вычислить a2, ε2, I2, считать момент сил трения постоянным и вычисленным при первом измерении. 7. Проверить соотношение: 8. 9. Сравнить значение I 2 с вычисленным по формуле (2.32). 10. Результаты измерений и вычислений записать в таблицу 2.1.
Таблица 2.1
2.4 Контрольные вопросы
1. Сформулируйте определение момента силы. Что называется плечом силы? 2. Сформулируйте и выведите закон динамики вращательного движения. 3. Каков физический смысл момента инерции и от чего он зависит? 4. Какие законы положены в основу вывода рабочей формулы? Выведите рабочую формулу. 5. Как в данной работе определяется момент сил трения? 6. Какова связь между линейными и угловыми скоростями и ускорениями? 7. На основании какой закономерности вычисляется ускорение падающего груза? 8. Почему нельзя допускать раскачивания груза, подвешенного на нити, при его движении вниз? На что и как это будет влиять?
Техника безопасности
1. Перед выполнением работы проверить прочность закрепления стержней и грузов на установке. 2. В процессе выполнения работы следите за тем, чтобы грузы не соскальзывали со стержней. 3. После окончания работы снимите грузы с крестовины.
Основные понятия и закономерности
Вращательное движение характеризуется угловым перемещением φ, угловой скоростью Связь линейного и углового перемещений выражается соотношением:
Тогда
При вращении твердого тела относительно неподвижной оси отдельные его элементарные части с массами
Кинетическая энергия вращающегося тела Wк определяется как сумма кинетических энергий его составных элементарных масс:
Величину, равную произведению элементарной массы
Момент инерции всего твердого тела относительно данной оси вращения равен сумме моментов инерции элементарных масс, составляющих данное тело:
Измеряется момент инерции в кг·м2. Более точно момент инерции можно определить при
где интегрирование производится по всему объему тела. Из формул (3.5) и (3.7) следует выражение кинетической энергии вращающегося твердого тела:
Момент инерции является основной физической величиной, характеризующей инертность твердого тела при вращательном движении. Момент инерции тела зависит от распределения массы рассматриваемого тела относительно заданной оси вращения (от формы и размеров тела и от расположения оси, относительно которой определяется момент инерции). Для однородных тел правильной геометрической (симметричной) формы момент инерции относительно осей симметрии легко вычисляется. Рассмотрим момент инерции некоторых тел правильной формы относительно оси симметрии ОО/: 1) Момент инерции материальной точки, т.е. тела, размеры которого много меньше расстояния до оси вращения. Масса тела m,расстояние до оси вращения ОО/ d (рисунок 3.2):
2) Момент инерции тонкостенных колец, цилиндра и обруча относительно оси ОО/ (ri= R) (рисунок 3.3):
где R – его радиус.
Рисунок 3.3
3) Момент инерции однородного сплошного цилиндра, диска относительно оси ОО/:
где m – масса диска; R – его радиус.
4) Момент инерции толстостенного кольца относительно оси кольца (рисунок 3.3):
где m – масса кольца; R1 – внутренний радиус; R2 – внешний радиус.
5) Момент инерции однородного шара относительно оси, проходящей через центр шара:
где m – масса шара; R – радиус шара.
6) Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно длине l:
где m – масса стержня; l – длина стержня.
Из приведенных выше выражений вытекает, что значения моментов инерции тел относительно оси симметрии, проходящей через центр масс, можно представить в виде:
где α – коэффициент пропорциональности, зависящий от формы тела. Если известен момент инерции I0 данного тела относительно оси, проходящей через центр масс этого тела ОО/, то момент инерции I этого тела относительно любой другой оси ХХ/, параллельной первой и отстоящей от нее на расстоянии а, вычисляется по теореме Штейнера (теорема о влиянии на момент инерции переноса оси вращения)
где m – масса тела. Эта теорема может быть выведена непосредственно из определения момента инерции тела относительно произвольной оси (рисунок 3.8).
Порядок выполнения работы
3.3.1 Определение момента инерции некоторых тел относительно оси, проходящей через их центр масс.
Определение момента инерции ненагруженной платформы маятника In. Сообщить платформе вращающий импульс (верхний диск резко повернуть на малый угол φ<50). Измерить секундомером время t, N полных колебаний (N =20-30) и вычислить период одного полного колебания:
Зная величины R, r, l, mn, вычислить по формуле (3.27) момент инерции платформы и сравнить с теоретическим значением (выражение 3.12).
3.3.2 Проверка теоремы Штейнера
1) Определение момента инерции двух цилиндров I2ц относительно оси ОО/, проходящей через их центр масс. Установить цилиндры друг на друга так, чтобы ось вращения проходила через их центр масс (рисунок 3.11). Измерить период колебаний системы, а затем по формуле (3.28) рассчитать момент инерции системы I1. Вычислить момент инерции двух цилиндров по формуле (3.29), а одного – по формуле:
Сравнить его с теоретическим значением (3.12).
2) Установить цилиндры симметрично относительно оси ОО/ на расстоянии d (рисунок 3.11). Определить период колебаний системы. Вычислить момент инерции системы по формуле (3.28) и момент инерции двух цилиндров
Определить момент инерции одного цилиндра:
Сравнить полученное значение
где mц – масса цилиндра. 3) Вывести формулы абсолютной и относительной погрешности для платформы без тела. Вычислить погрешность измерения для ненагруженной платформы по формуле погрешности. Все измерения и вычисления занести в таблицу 3.1.
Таблица 3.1
3.4 Контрольные вопросы
1) Что называется моментом инерции? В каких единицах он измеряется? 2) Какой закон положен в основу рабочей формулы? Выведите рабочую формулу. 3) В чем отличие крутильных колебаний от колебаний физического маятника? 4) Почему натяжение нитей трифилярного подвеса должно быть одинаковым? 5) Сформулируйте теорему Штейнера. 6) Под действием какой силы трифилярный подвес совершает крутильные колебания? 7) Выведите формулу погрешности
Техника безопасности
1. Перед работой проверить натяжение нитей трифилярного подвеса и положение нижнего и верхнего дисков. 2. После выполнения работы снять грузы с нижней платформы.
Основные понятия и закономерности
Примером применения законов сохранения импульса и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел. Удар (или соударени
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.013 с.) |

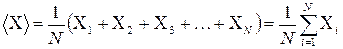 (1.2)
(1.2)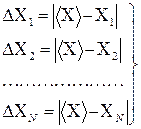 (1.3)
(1.3)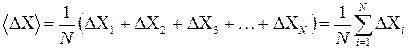 (1.4)
(1.4)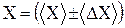 ед. изм. (1.5)
ед. изм. (1.5)
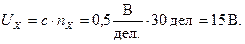
 , который соответствует
, который соответствует 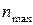 – делений шкалы, рассчитать цену деления
– делений шкалы, рассчитать цену деления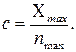 (1.6)
(1.6)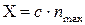 . (1.7)
. (1.7)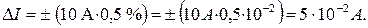
 , то абсолютная погрешность во всех случаях одинакова
, то абсолютная погрешность во всех случаях одинакова 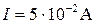 . Результаты измерений:
. Результаты измерений: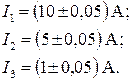
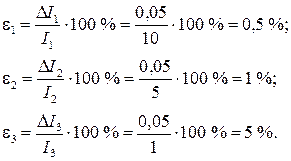
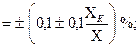 (1.8)
(1.8)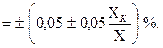 (1.9)
(1.9) , т.е. D d = ±0,005мм. При измерении температуры термометром с ценой деления шкалы 2оС погрешность составит
, т.е. D d = ±0,005мм. При измерении температуры термометром с ценой деления шкалы 2оС погрешность составит  . В случае измерения тока или напряжения определяется цена деления прибора согласно выбранному пределу, а затем абсолютная погрешность измерения по классу точности прибора.
. В случае измерения тока или напряжения определяется цена деления прибора согласно выбранному пределу, а затем абсолютная погрешность измерения по классу точности прибора. .
.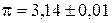 или
или 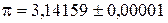 .
. ,
, 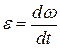 или
или  , (2.1)
, (2.1)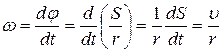 ;
; 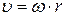 , (2.2)
, (2.2) ;
; 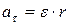 , (2.3)
, (2.3) направлен по оси вращения так, что из его конца вращение видно происходящим против часовой стрелки (правый винт, рисунок 2.1,а).
направлен по оси вращения так, что из его конца вращение видно происходящим против часовой стрелки (правый винт, рисунок 2.1,а). совпадает с направлением вектора
совпадает с направлением вектора  , если
, если 
 , равная векторному произведению радиуса-вектора
, равная векторному произведению радиуса-вектора  (проводится от центра вращения точки О в точку приложения силы, точку А) на вектор силы
(проводится от центра вращения точки О в точку приложения силы, точку А) на вектор силы  (рисунок 2.2)
(рисунок 2.2)
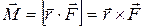 , (2.4)
, (2.4)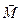 – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от
– псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 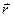 к
к  (рисунок 2.2). Векторы
(рисунок 2.2). Векторы 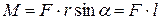 , (2.5)
, (2.5)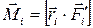 , (2.6)
, (2.6)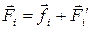 – сумма внутренних
– сумма внутренних 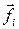 и внешних
и внешних 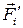 сил, действующих на отдельную точку i (рисунок 2.3).
сил, действующих на отдельную точку i (рисунок 2.3).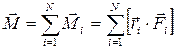 (2.7)
(2.7)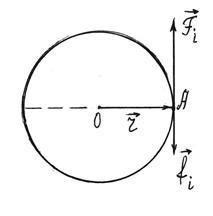
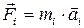 , где
, где 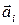 – линейное ускорение материальной точки, связанное с угловым ускорением
– линейное ускорение материальной точки, связанное с угловым ускорением  , (2.8)
, (2.8)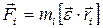 , а момент силы
, а момент силы  равен
равен , (2.9)
, (2.9)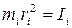 – момент инерции материальной точки равен произведению массы точки mi на квадрат расстояния ri от оси вращения в точке О до точки А.
– момент инерции материальной точки равен произведению массы точки mi на квадрат расстояния ri от оси вращения в точке О до точки А.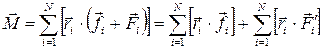 , (2.10)
, (2.10)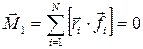 – вращающий момент внутренних сил равен нулю (по третьему закону Ньютона).
– вращающий момент внутренних сил равен нулю (по третьему закону Ньютона). , (2.11)
, (2.11)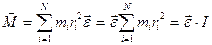 , (2.12)
, (2.12) – момент инерции твердого тела относительно данной оси вращения.
– момент инерции твердого тела относительно данной оси вращения.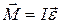 . (2.13)
. (2.13)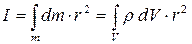 , (2.14)
, (2.14) – бесконечно малая масса тела.
– бесконечно малая масса тела.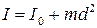 (2.15)
(2.15)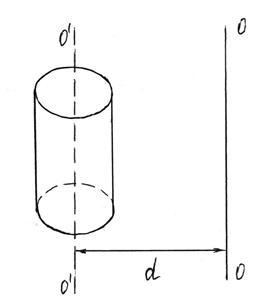

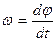 и угловым ускорением
и угловым ускорением 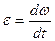 . При вращательном движении все точки тела имеют одинаковую угловую скорость и угловое ускорение.
. При вращательном движении все точки тела имеют одинаковую угловую скорость и угловое ускорение.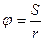 (радиан) (3.1)
(радиан) (3.1)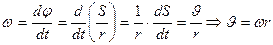 (3.2)
(3.2) (3.3)
(3.3) (материальные точки) описывают окружности разных радиусов ri и имеют различные линейные скорости
(материальные точки) описывают окружности разных радиусов ri и имеют различные линейные скорости  . Но угловая скорость вращения
. Но угловая скорость вращения 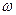 всех этих точек, если тело при вращении не деформируется, одинакова, т.е.
всех этих точек, если тело при вращении не деформируется, одинакова, т.е. (3.4)
(3.4)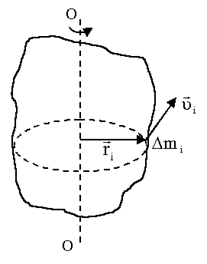
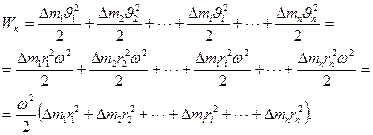 (3.5)
(3.5) , называют моментом инерции материальной точки
, называют моментом инерции материальной точки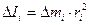 (3.6)
(3.6)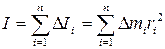 (3.7)
(3.7)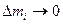 :
: , (3.8)
, (3.8)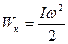 (3.9)
(3.9)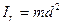 (3.10)
(3.10)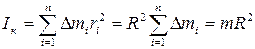 , (3.11)
, (3.11) – масса тела;
– масса тела;
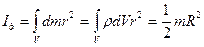 , (3.12)
, (3.12)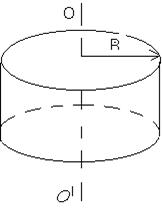
 , (3.13)
, (3.13)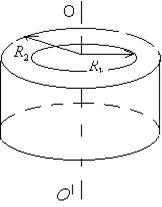
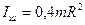 , (3.14)
, (3.14)
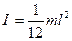 , (3.15)
, (3.15)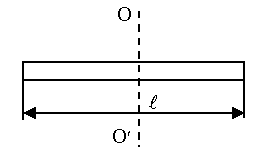
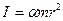 , (3.16)
, (3.16) , (3.17)
, (3.17)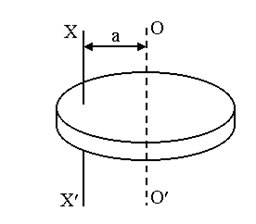
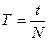 . (3.30)
. (3.30) (3.31)
(3.31)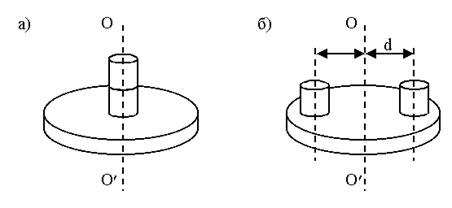
 :
: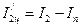 .
.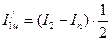 .
. с вычисленным по теореме Штейнера:
с вычисленным по теореме Штейнера: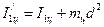 ,
,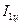 – момент инерции одного цилиндра относительно оси, проходящей через центр масс (формула 3.31),
– момент инерции одного цилиндра относительно оси, проходящей через центр масс (формула 3.31), для момента инерции платформы.
для момента инерции платформы.


