Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа. Определение момента инерции различных тел методом крутильных колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: определение момента инерции тел правильной геометрической формы методом крутильных колебаний.
Основные понятия и закономерности
Вращательное движение характеризуется угловым перемещением φ, угловой скоростью Связь линейного и углового перемещений выражается соотношением:
Тогда
При вращении твердого тела относительно неподвижной оси отдельные его элементарные части с массами
Кинетическая энергия вращающегося тела Wк определяется как сумма кинетических энергий его составных элементарных масс:
Величину, равную произведению элементарной массы
Момент инерции всего твердого тела относительно данной оси вращения равен сумме моментов инерции элементарных масс, составляющих данное тело:
Измеряется момент инерции в кг·м2. Более точно момент инерции можно определить при
где интегрирование производится по всему объему тела. Из формул (3.5) и (3.7) следует выражение кинетической энергии вращающегося твердого тела:
Момент инерции является основной физической величиной, характеризующей инертность твердого тела при вращательном движении. Момент инерции тела зависит от распределения массы рассматриваемого тела относительно заданной оси вращения (от формы и размеров тела и от расположения оси, относительно которой определяется момент инерции). Для однородных тел правильной геометрической (симметричной) формы момент инерции относительно осей симметрии легко вычисляется. Рассмотрим момент инерции некоторых тел правильной формы относительно оси симметрии ОО/: 1) Момент инерции материальной точки, т.е. тела, размеры которого много меньше расстояния до оси вращения. Масса тела m,расстояние до оси вращения ОО/ d (рисунок 3.2):
2) Момент инерции тонкостенных колец, цилиндра и обруча относительно оси ОО/ (ri= R) (рисунок 3.3):
где R – его радиус.
Рисунок 3.3
3) Момент инерции однородного сплошного цилиндра, диска относительно оси ОО/:
где m – масса диска; R – его радиус.
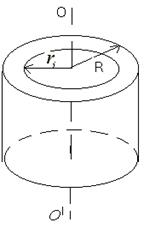
4) Момент инерции толстостенного кольца относительно оси кольца (рисунок 3.3):
где m – масса кольца; R1 – внутренний радиус; R2 – внешний радиус.
5) Момент инерции однородного шара относительно оси, проходящей через центр шара:
где m – масса шара; R – радиус шара.
6) Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно длине l:
где m – масса стержня; l – длина стержня.
Из приведенных выше выражений вытекает, что значения моментов инерции тел относительно оси симметрии, проходящей через центр масс, можно представить в виде:
где α – коэффициент пропорциональности, зависящий от формы тела. Если известен момент инерции I0 данного тела относительно оси, проходящей через центр масс этого тела ОО/, то момент инерции I этого тела относительно любой другой оси ХХ/, параллельной первой и отстоящей от нее на расстоянии а, вычисляется по теореме Штейнера (теорема о влиянии на момент инерции переноса оси вращения)
где m – масса тела. Эта теорема может быть выведена непосредственно из определения момента инерции тела относительно произвольной оси (рисунок 3.8).
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |

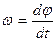 и угловым ускорением
и угловым ускорением 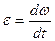 . При вращательном движении все точки тела имеют одинаковую угловую скорость и угловое ускорение.
. При вращательном движении все точки тела имеют одинаковую угловую скорость и угловое ускорение.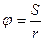 (радиан) (3.1)
(радиан) (3.1)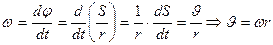 (3.2)
(3.2) (3.3)
(3.3) (материальные точки) описывают окружности разных радиусов ri и имеют различные линейные скорости
(материальные точки) описывают окружности разных радиусов ri и имеют различные линейные скорости  . Но угловая скорость вращения
. Но угловая скорость вращения 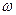 всех этих точек, если тело при вращении не деформируется, одинакова, т.е.
всех этих точек, если тело при вращении не деформируется, одинакова, т.е. (3.4)
(3.4)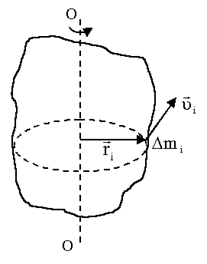
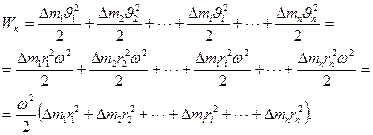 (3.5)
(3.5) , называют моментом инерции материальной точки
, называют моментом инерции материальной точки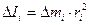 (3.6)
(3.6)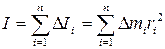 (3.7)
(3.7)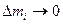 :
: , (3.8)
, (3.8)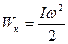 (3.9)
(3.9)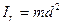 (3.10)
(3.10)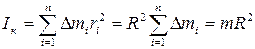 , (3.11)
, (3.11) – масса тела;
– масса тела;
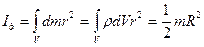 , (3.12)
, (3.12)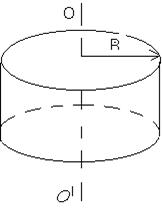
 , (3.13)
, (3.13)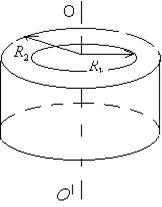
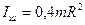 , (3.14)
, (3.14)
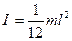 , (3.15)
, (3.15)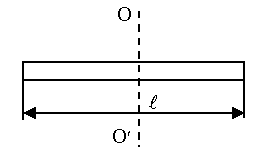
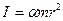 , (3.16)
, (3.16) , (3.17)
, (3.17)