
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неинерциальные системы отсчета.Содержание книги
Поиск на нашем сайте Силы инерции
Как уже отмечалось (см. § 5, 6), законы Ньютона выполняются только в инерциальных системах отсчета. Системы отсчета, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными. В неинерциальных системах законы Ньютона, вообще говоря, уже несправедливы. Однако законы динамики можно применять и для них, если кроме сил, обусловленных воздействием тел друг на друга, ввести в рассмотрение силы особого рода — так называемые силы терцин. Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции). Силы инерции Fинпри этом должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение а', каким оно обладает в неинерциальных системах отсчета, т. е.
Так как F = ma (а — ускорение тела в инерциальной системе отсчета), то
Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, поэтому в общем случае нужно учитывать следующие случаи проявления этих сил: 1) силы инерции при ускоренном поступательном движении системы отсчета; 2) силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета; 3) силы инерции, действующие на тело, движущееся во вращающейся системе отсчета. Рассмотрим эти случаи. 1. Силы терцин при ускоренном поступательном движения системы отсчета. Пусть на тележке к штативу на нити подвешен шарик массой т (рис. 40). Пока тележка покоится или движется равномерно и прямолинейно, вить, удерживающая шарик, занимает вертикальное положение и сила тяжести Р уравновешивается силой реакции нити Т.
Рис. 40
Если тележку привести в поступательное движение с ускорением «о, то нить начнет отклоняться от вертикали назад до такого угла а, пока результирующая сила F = P + T не обеспечит ускорение шарика, равное oq. Таким образом, результирующая сила F направлена в сторону ускорения тележки iq и для установившегося движения шарика (шарик теперь движется вместе с тележкой с ускорением а0) равна F = mg tg a = ma0, откуда
т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки. Относительно системы отсчета, связанной с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой Fи, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом,
Проявление сил инерции при поступательном движении наблюдается в повседневных явлениях. Например, когда поезд набирает скорость, то пассажир, сидящий по ходу поезда, под действием силы инерции прижимается к спинке сиденья. Наоборот, при торможении поезда сила инерции направлена в противоположную сторону и пассажир удаляется от спинки сиденья. Особенно эти силы заметны при внезапном торможении поезда. Силы инерции проявляются в перегрузках, которые возникают при запуске и торможении космических кораблей. 2. Силы инерции, действующее на тело, покоящееся во вращающейся системе отсчета. Пусть диск равномерно вращается с угловой скоростью w (w —const) вокруг вертикальной оси, проходящей через его центр. На диске, на разных расстояниях от оси вращения, установлены маятники (на нитях подвешены шарики массой т). При вращении маятников вместе с диском шарики отклоняются от вертикали на некоторый угол (рис. 41).
Рис. 41
В инерциальной системе отсчета, связанной, например, с помещением, где установлен диск, шарик равномерно вращается по окружности радиусом R(расстояние от центра вращающегося шарика до оси вращения). Следовательно, на него действует сила, равная F = mw2R и направленная перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести Р и силы натяжения нити Т: F = P + T. Когда движение шарика установится, то F = mg tg a =mw2R, откуда
т.e. углы отклонения нитей маятников будут тем больше, чем больше расстояние R от центра шарика до оси вращения диска и чем больше угловая скорость вращения w. Относительно системы отсчета, связанной с вращающимся диском, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой Fц, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Сила Fц, называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна
Действие центробежных сил инерции подвергаются, например, пассажиры в движущемся транспорте на поворотах, летчики при выполнении фигур высшего пилотажа; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах и т. д., где они достигают огромных значений. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов и т. д.) принимаются специальные меры для уравновешивания центробежных сил инерции. Из формулы (27.3) вытекает, что центробежная сила инерции, действующая на тела во вращающихся системах отсчета в направлении радиуса от оси вращения, зависит от угловой скорости вращения со системы отсчета и радиуса R, во не зависит от скорости тел относительно вращающихся систем отсчета. Следовательно, центробежная сила инерции действует во вращающихся системах отсчета на все тела, удаленные от оси вращения на конечное расстояние, независимо от того, покоятся ли они в этой системе (как мы предполагали до сих пор) или движутся относительно нее с какой-то скоростью. 3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета. Пусть шарик массой т движется спостоянной скоростью v' вдоль радиуса равномерно вращающегося диска (v' = const, w = const, v'^w). Если диск не вращается, то шарик, направленный вдоль радиуса, движется по радиальной прямой и попадает в точку А, если же, диск привести во вращение в направлении, указанном стрелкой, то шарик катится по кривой ОБ (рис. 42, а), причем его скорость v' относительно диска изменяет свое направление. Это возможно лишь тогда, если на шарик действует сила, перпендикулярная скорости v'.
Рис. 42
Для того чтобы заставить шарик катиться по вращающемуся диску вдоль радиуса, используем жестко укрепленный вдоль радиуса диска стержень, на котором шарик движется без трения равно мерно и прямолинейно со скоростью v' (рис. 42, б). При отклонении шарика стержень действует на него с некоторой силой F. Относительно диска (вращающейся системы отсчета) шарик движется равномерно и прямолинейно, что можно объяснить тем, что сила F уравновешивается приложенной к шарику силой инерции FK, перпендикулярной скорости v'. Эта сила называется кориолисовой силой инерции. Можно показать, что сила Кориолиса*
Вектор FK перпендикулярен векторам скорости v¢ тела и угловой скорости вращения wсистемы отсчета в соответствии с правилом правого винта. Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. Поэтому действием этих сил объясняется ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север (рис. 43), то действующая на него сила Кориолиса, как это следует из выражения (27.4), будет направлена вправо по отношению к направлению движения, т. е. тело несколько отклонится на восток. Если тело движется на юг, то сила Кориолиса также действует вправо, если смотреть по направлению движения, т. е. тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые и т.д. Аналогично можно показать, что в южном полушарии сила Кориолиса, действующая на движущиеся тела, будет направлена влево по отношению к движению.
Рис. 43
Благодаря силе Кориолиса, падающие на поверхность Земли тела отклоняются к востоку (на широте 60° это отклонение должно составлять 1 см при падении с высоты 100 м). С силой Кориолиса связано поведение маятника Фуко, явившееся в свое время одним из доказательств вращения Земли. Если бы этой силы не было, то плоскость колебаний качающегося вблизи поверхности Земли маятника оставалась бы неизменной (относительно Земли). Действие же сил Кориолиса приводит к вращению плоскости колебаний вокруг вертикального направления. Раскрывая содержание Fин в формуле (27.1), получим основной закон динамики для инерциальных систем отсчета:
где силы инерции задаются формулами (27.2) — (27.4). Обратим еще раз внимание на то, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу. Два основных положения механики, согласно которым ускорение всегда вызывается силой, а сила всегда обусловлена взаимодействием между телами, в системах отсчета, движущихся с ускорением, одновременно не выполняются. Для любого из тел, находящихся в неинерциальной системе отсчета, силы инерции являются внешними; следовательно, здесь нет замкнутых систем. Это означает, что в неинерциальных системах отсчета не выполняются законы сохранения импульса, энергии и момента импульса. Таким образом, силы инерции действуют только в неинерциальных системах. В инерциальных системах отсчета таких сил не существует. Возникает вопрос о «реальности» или «фиктивности» сил инерции. В ньютоновской механике, согласно которой сила есть результат взаимодействия тел, на силы инерции можно смотреть как на «фиктивные», «исчезающие» в инерциальных системах отсчета. Однако возможна и другая их интерпретация. Так как взаимодействия тел осуществляются посредством силовых полей, то силы инерции рассматриваются как воздействия, которым подвергаются тела со стороны каких-то реальных силовых полей, и тогда их можно считать «реальными». Независимо от того, рассматриваются ли силы инерции в качестве «фиктивных» или «реальных», многие явления, о которых упоминалось в настоящем параграфе, объясняются с помощью сил инерции. Силы инерции, действующие на тела в неинерциальной системе отсчета, пропорциональны их массам и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в «поле сил инерции» эти тела движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают тела, находящиеся под действием сил поля тяготения. При некоторых условиях силы инерции и силы тяготения невозможно различить. Например, движение тел в равноускоренном лифте происходит точно так же, как и в неподвижном лифте, висящем в однородном поле тяжести. Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции. Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сип и сил инерции (принципа эквивалентности Эйнштейна): все физические явления в поле тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы. Этот принцип является основой общей теории относительности.
Задачи
5.1. Два одинаковых однородных шара из одинакового материала, соприкасаясь друг с другом, притягиваются. Определить, как изменится сила притяжения, если массу шаров увеличить в n=4 раза. [Возрастет в 6,35 раза]
5.2. Плотность вещества некоторой шарообразной планеты составляет 3 г/см3. Каким должен быть период обращения планеты вокруг собственной оси, чтобы на экваторе тела были невесомыми? [r = Ö3p/(Gp)=1,9 ч]
5.3. Определить, в какой точке (считая of Земли) на прямой, соединяющей центры Земли и Луны, напряженность поля тяготения равна нулю. Расстояние между центрами Земли и Луны равно R, масса Земли в 81 раз больше массы Луны. [0,9 R]
5.4. Два одинаковых однородных шара из одинакового материала соприкасаются друг с другом. Определить, как изменится потенциальная энергия их гравитационного взаимодействия, если массу шаров увеличить в четыре раза. [Возрастет в 14,6 раза]
5.5. Два спутника одинаковой массы движутся вокруг Земли по круговым орбитам радиусов R1 и R2. Определить: 1) отношение полных энергий спутников (Е1/Е2); 2) отношение их моментов импульса (L1/L2).[1) R2/R1; 2)
5.6. Вагон катится вдоль горизонтального участка дороги. Сила трения составляет 20% от веса вагона. К потолку вагона на нити подвешен шарик массой 10 г. Определить: 1) силу, действующую на нить; 2) угол отклонения нити от вертикали. [1) 0,10 Н; 2) 11°35']
5.7. Тело массой 1,5 кг, падая свободно в течение 5 с, попадает на Землю в точку с географической широтой j=45°. Учитывая вращение Земли, нарисовать и определить все силы, действующие на тело в момент его падения на Землю. [1) 14,7 Н; 2) 35,7 Н; 3) 7,57 мН]
Глава 6 Элементы механики жидкостей
Давление в жидкости и газе
Молекулы газа, совершая беспорядочное, хаотическое движение, не связаны или весьма слабо связаны силами взаимодействия, поэтому они движутся свободно и в результате соударений стремятся разлететься во все стороны, заполняя весь предоставленный им объем, т. е. объем газа определяется объемом того сосуда, который газ занимает. Жидкость же, имея определенный объем, принимает форму того сосуда, в который она заключена. Но в жидкостях в отличие от газов среднее расстояние между молекула ми остается практически постоянным, поэтому жидкость обладает практически неизменным объемом. Свойства жидкостей и газов во многом отличаются, однако в ряде механических явлений их поведение определяется одинаковыми параметрами и идентичными уравнениями. Поэтому гидроаэромеханика — раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми ими твердыми телами, — использует единый подход к изучению жидкостей и газов. В механике с большой степенью точности жидкости и газы рассматриваются как сплошные, непрерывно распределенные в занятой ими части пространства. Плотность же газов от давления зависит существенно. Из опыта известно, что сжимаемостью жидкости и газа во многих задачах можно пренебречь и пользоваться единым понятием несжимаемой жидкости — жидкости, плотность которой всюду одинакова и не изменяется со временем. Если в покоящуюся жидкость поместить тонкую пластинку, то части жидкости, находящиеся по разные стороны от нее, будут действовать на каждый ее элемент Д5 с силами AF, которые независимо от того, как пластинка ориентирована, будут равны по модулю и направлены перпендикулярно площадке DS, так как наличие касательных сил привело бы частицы жидкости в движение (рис. 44).
Рис. 44
Физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади, называется давлением р жидкости:
Единица давления — паскаль (Па): 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м2 (1 Па=1 Н/м2). Давление при равновесии жидкостей (газов) подчиняется закону Паскаля*: давление в любом месте покоящейся жидкости одинаково по всем направлениям, при чем давление одинаково передается по всему объему, занятому покоящейся жидкостью. Рассмотрим, как влияет вес жидкости на распределение давления внутри покоящейся несжимаемой жидкости. При равновесии жидкости давление по горизонтали всегда одинаково, иначе не было бы равновесия. Поэтому свободная поверхность покоящейся жидкости всегда горизонтальна вдали от стенок сосуда. Если жидкость несжимаема, то ее плотность не зависит от давления. Тогда при поперечном сечении S столба жид кости, его высоте h и плотности rвес P = rgSh,а давление на нижнее основание
т. е. давление изменяется линейно с высотой. Давление rghназывается гидростатическим давлением. Согласно формуле (28.1), сила давления на нижние слои жидкости будет больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа):
где r— плотность жидкости, V— объем погруженного в жидкость тела.
Уравнение неразрывности
Движение жидкостей называется течением, а совокупность частиц движущейся жид кости — потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 45). Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы.
Рис. 45
Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются. Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2,перпендикулярные направлению скорости (рис. 46).
Рис. 46
За время Dt через сечение S проходит объем жидкости SvDt; следовательно, за 1 с через S1 пройдет объем жидкости S1v1, где v1— скорость течения жидкости в месте сечения S1.Через сечение S2 за 1 с пройдет объем жидкости S2v2, где v2 — скорость течения жидкости в месте сечения S2. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (r=const), то через сечение S2пройдет такой же объем жидкости, как и через сечение S1 ъ т. е.
Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение (29.1) называется уравнением неразрывности для несжимаемой жидкости.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 751; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |


 (27.1)
(27.1)

 (27.2)
(27.2)

 (27.3)
(27.3)
 (27.4)
(27.4)

 ]
]
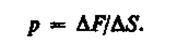
 (28.1)
(28.1)


 (29.1)
(29.1)


