
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение теоремы Гаусса к расчетуСодержание книги
Поиск на нашем сайте
Некоторых электростатических полей В вакууме
1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью +s (s = dQ/dS— заряд, приходящийся на единицу поверхности).
Рис. 126
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cosa = 0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Enсовпадает с E), т. е. равен 2ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен sS.Согласно теореме Гаусса (81.2), 2ES = sS/e0, откуда
Из формулы (82.1) вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.. 2. Поле двух бесконечных параллельных разноименно зараженных плоскостей (рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями + aи — a. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E = 0. В области между плоскостями Е = Е+ + Е_ (Е+и E_ определяются по формуле (82.1)), поэтому результирующая напряженность
Рис. 127
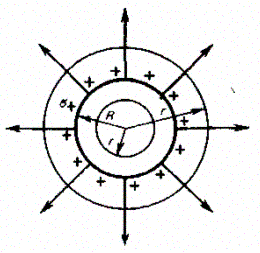
Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой (82.2), а вне объема, ограниченного плоскостями, равна нулю. 3. Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R собщим зарядом Qзаряжена равномерно с поверхностной плотностью + s. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис. 128).
Рис. 128
Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если г > R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (81.2), 4pr2E = Q/e0,откуда
При r>Rполе убывает с расстоянием rпо такому же закону, как у точечного заряда. График зависимости E от г приведен на рис. 129. Если r¢ < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (Е = 0).
Рис. 129
4. Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью r (
Таким образом, напряженность поля вне равномерно заряженного шара описывается формулой (82.3), а внутри его изменяется линейно с расстоянием / согласно выражению (82.4). График зависимости Е от гдля рассмотренного случая приведен на рис. 130.
Рис. 130
5. Поле равномерно зараженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R(рис. 131) заряжен равномерно с линейной плотностью t (
Рис. 131
Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса rи высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен 2pr l E. По теореме Гаусса (81.2), при r > R 2pr l E = t l /e0, откуда
Если г < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области E = 0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (82.5), внутри же его поле отсутствует.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.005 с.) |


 (82.1)
(82.1) (82.2)
(82.2)
 (82.3)
(82.3)
 - заряд, приходящийся на единицу объема). Учитывая соображения симметрии (см. п. 3), можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (82.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса r' < Rохватывает заряд G' = 4/3pr¢3r. Поэтому, согласно теореме Гаусса (81.2),
- заряд, приходящийся на единицу объема). Учитывая соображения симметрии (см. п. 3), можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (82.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса r' < Rохватывает заряд G' = 4/3pr¢3r. Поэтому, согласно теореме Гаусса (81.2),  Учитывая, что
Учитывая, что  , получаем
, получаем (82.4)
(82.4)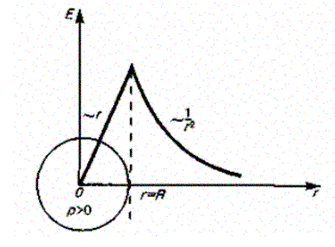
 - заряд, приходящийся на единицу длины).
- заряд, приходящийся на единицу длины).
 (82.5)
(82.5)


