
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое представление энергииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Во многих задачах рассматривается одномерное движение тела, потенциальная энергия которого является функцией лишь одной переменной (например, координаты х), т. е. П = П(х).График зависимости потенциальной энергии от некоторого аргумента называется потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела. Будем рассматривать только консервативные системы, т. е. системы, в которых взаимные превращения механической энергии в другие виды отсутствуют. Тогда справедлив закон сохранения энергии в форме (13.3). Рассмотрим графическое представление потенциальной энергии для тела в однородном поле тяжести и для упругодеформированного тела. Потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, согласно (12.7), П (h)=mgh. График данной зависимости П = П(h) — прямая линия, проходящая через начало координат (рис. 15), угол наклона которой к оси h тем больше, чем больше масса тела (так как tg a = mg).
Рис. 15
Пусть полная энергия тела равна Е (ее график — прямая, параллельная оси К). На высоте h тело обладает потенциальной энергией П, которая определяется отрезком вертикали, заключенным между точкой h на оси абсцисс и графиком П(h). Естестве но, что кинетическая энергия Т задается ординатой между графиком П(h)и горизонтальной прямой ЕЕ. Из рис. 15 следует, что если h=hmax, то Т=0и П = E = mghmax,т. е. потенциальная энергия становится максимальной и равной полной энергии. Из приведенного графика можно найти скорость тела на высоте h:
Зависимость потенциальной энергии упругой деформации H=kx2/2от деформации х имеет вид параболы (рис. 16), где график заданной полной энергии тела Е — прямая, параллельная оси абсцисс х, а значения Г и П определяются так же, как на рис. 15. Из рис. 16 следует, что с возрастанием деформации х потенциальная энергия тела воз растает, а кинетическая — уменьшается. Абсцисса xmax определяет максимально возможную деформацию растяжения тела, а — хmax — максимально возможную деформацию сжатия тела. Если х = ± xmax, то Т = 0 и П = E = kx2max/2,т. е. потенциальная энергия становится максимальной и равной полной энергии. Из анализа графика на рис. 16 вытекает, что при полной энергии тела, равной Е, тело не может сместиться правее xmaxи левее — xmax, так как кинетическая энергия не может быть отрицательной и, следовательно, потенциальная энергия не может быть больше полной энергии. В таком случае говорят, что тело находится в потенциальной яме с координатами - xmax £ x £ xmax
Рис. 16
В общем случае потенциальная кривая может иметь довольно сложный вид, например с несколькими чередующимися максимумами и минимумами (рис. 17). Проанализируем эту потенциальную кривую. Если Е — заданная полная энергия частицы, то частица может находиться только там, где П(x) £ E, т. е. в областях I и III. Переходить из области I в III и обратно частица не может, так как ей препятствует потенциальный барьер CDG, ширина которого равна интервалу значений х, при которых Е < П, а его высота определяется разностью Пmax - E. Для того чтобы частица смогла преодолеть потенциальный барьер, ей необходимо сообщить дополнительную энергию, равную высоте барьера или превышающую ее. В области I частица с полной энергией Е оказывается «запертой» в потенциальной яме ABC и совершает колебания между точками с координатами x а и хс.
Рис. 17
В точке В с координатой х0 (рис. 17) потенциальная энергия частицы минимальна. Так как действующая на частицу сила (см. § 12) При смещении частицы из положения х0 (и влево и вправо) она испытывает действие возвращающей силы, поэтому положение х0 является положением устойчивого равновесия. Указанные условия выполняются и для точки х¢0 (для Пmax). Однако эта точка соответствует положению неустойчивого равновесия, так как при смещении частицы из положения х'0 появляется сила, стремящаяся удалить ее от этого положения.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |






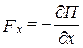 (П— функция только одной координаты), а условие минимума потенциальной энергии
(П— функция только одной координаты), а условие минимума потенциальной энергии  , то в точке В – Fx = 0.
, то в точке В – Fx = 0.


