
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутренняя энергия идеального газа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Равномерное распределение энергии по степеням свободы молекул Внутренняя энергия системы - энергия, зависящая Числом степеней свободы тела называется число независимых координат, полностью определяющих положение тела в пространстве. Если одноатомную молекулу рассмат- ривать как материальную точку, то для описания её положения в пространстве достаточно трёх независимых координат. Следовательно, одноатомная молекула имеет три степени свободы. Двухатомная молекула с жёсткой связью между атомами имеет пять степеней свободы. Три из них определяют поступательное движение молекулы, две - вращательное. Если в молекуле три (и более) атома, связанных жёсткой связью, то число степеней свободы равно 6. Во многих случаях необходи- мо принимать во внимание возможность относительных смещений атомов в молекуле, т.е. вводить в рассмотрение колебательные степени свободы молекул. Согласно закону Больцмана о равномерном распределе- нии энергии по степеням свободы молекул все степени свободы равноправны и вносят одинаковый вклад в ее сред- нюю энергию. Учитывая, что средняя энергия поступатель- ного движения одноатомной молекулы по формуле (2.7), равна
получим кинетическую энергию, приходящуюся на одну степень свободы
Если молекула имеет ί степеней свободы, то ее средняя кинетическая энергия
где Колебательная степень обладает вдвое большей энергией поскольку на нее приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. С учетом (3.2), внутренняя энергия одного моля идеаль- ного газа равна
а произвольной массы газа
Таким образом, внутренняя энергия идеального газа зависит от числа степеней свободы молекул и абсолютной температуры. Внутренняя энергия – однозначная функция состояния системы, она не зависит от пути перехода в данное состояние. Изменение внутренней энергии газа связано с изменением температуры
Теплота и работа. Первое начало термодинамики
Внутренняя энергия системы может быть изменена только в результате взаимодействия системы с внешней средой. Такое взаимодействие может происходить двумя способами: путём теплообмена и путём совершения механической работы. Теплообмен - самопроизвольный необратимый процесс передачи энергии, происходящий в неоднородном темпера- турном поле. Существуют следующие способы теплообмена: а) теплопроводность - передача внутренней энергии от одних тел к другим при их соприкосновении, обусловленная тепловым движением атомов (молекул); б) конвекция - перенос энергии, происходящий при перемешивании неодинаково нагретых слоев газа или жидкости под действием силы тяжести и выталкивающей силы; в) излучение - передача внутренней энергии без участия промежуточной среды путём испускания и поглощения электро- магнитного излучения. Мерой энергии, передаваемой системе при теплообмене, служит количество теплоты Q. Элементарное приращение количества теплоты dQ > 0, если оно передаётся системе, и dQ < 0, если система отдаёт энергию. Отношение элементарного количества теплоты dQ, сообщаемого системе при бесконечно малом изменении её состояния в каком-либо процессе, к соответствующему изменению dT её абсолютной температуры, называется теплоёмкостью системы:
Таким образом, теплоёмкость системы численно равна количеству теплоты, которое необходимо сообщить системе, для её нагревания на 1 К. Удельная теплоёмкость - физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания на 1 К:
;.
.
Следует различать теплоёмкости cр , СР и cv, CV. Первые характеризуют теплообмен при постоянном давлении, а вторые - при постоянном объёме. Так как количество теплоты Q не является парамет- ром состояния термодинамической системы, то элементарное количество теплоты является не полным дифференциалом, поэтому его обозначают
Но состояние системы можно изменить и другим способом, совершая над системой работу или давая ей возможность самой совершать работу, то есть путём изменения макроскопических параметров системы. В качестве системы рассмотрим идеальный газ в сосуде с подвижным поршнем (рис 3.1). Если под действием силы
где P - давление газа, S - площадь поршня, dV = S dx приращение объёма газа. Элементарная работа
При расширении (сжатии) газа может изменяться не только объём, но и его давление. Поэтому, чтобы найти работу при конечном изменении объёма, нужно знать зависимость р(V). Тогда работа определяется интегралом
который численно равен площади заштрихованной фигуры (рис.3.2). Закон сохранения энергии в области тепловых явлений называется первым началом термодинамики: теплота, сообщаемая системе, затрачивается на увеличение внутрен- ней энергии системы и на работу, которую система совершает над внешней средой
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.152.33 (0.011 с.) |

 ,
, . (3.1)
. (3.1) , (3.2)
, (3.2) .
. , (3.3)
, (3.3) . (3.4)
. (3.4) . (3.5)
. (3.5)
 ;..
;..

 Молярная теплоёмкость - теплоёмкость одного моля вещества:
Молярная теплоёмкость - теплоёмкость одного моля вещества: Q (сравните: внутренняя энергия системы - функция состояния; малое изменение внутренней энергии - полный дифференциал dU).
Q (сравните: внутренняя энергия системы - функция состояния; малое изменение внутренней энергии - полный дифференциал dU). , с которой газ действует на поршень, последний переместился на расстояние dx, то газ совершил работу
, с которой газ действует на поршень, последний переместился на расстояние dx, то газ совершил работу
 ,
, - не полный дифференциал, так как работа зависит не только от начального и конечного состояния системы, но и от формы пути, по которому система переходит из одного состояния в другое, а значит А не является функцией состояния. Если газ расширяется, то dV>0 и, совершаемая им работа
- не полный дифференциал, так как работа зависит не только от начального и конечного состояния системы, но и от формы пути, по которому система переходит из одного состояния в другое, а значит А не является функцией состояния. Если газ расширяется, то dV>0 и, совершаемая им работа  А > 0, если сжимается - газ совершает отрицатель- ную работу,
А > 0, если сжимается - газ совершает отрицатель- ную работу,  А < 0.
А < 0.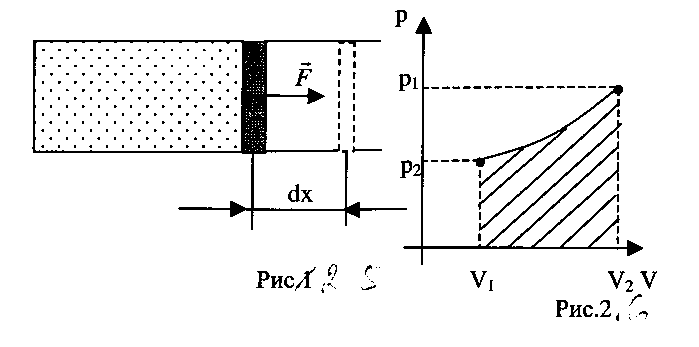
 , (3.6)
, (3.6) . (3.7)
. (3.7)


