
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выражение вектора через проекцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
на координатные оси:
где
1.3. Сложение векторов:
a) правило параллелограмма; в) правило треугольника.
1.4. Вычитание векторов
Скалярное произведение двух векторов
где a - угол между векторами В декартовой системе координат
Векторное произведение двух векторов
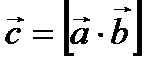 , , 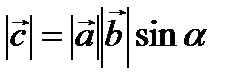 , ,
где a - угол между векторами Вектор образуют правую тройку векто- ров (правило правого винта).
Производная и дифференциал
2.1. Производная от функции y = ¦(x)
Геометрический смысл производной – она численно равна тангенсу угла наклона касательной к кривой y = ¦(x) в точке x. Если ¦¢(x) > 0, то при увеличении x функция ¦(x) - возрастает, если ¦¢(x) < 0, то при возрастании x функция ¦(x) - уменьшается.
Таблица простейших производных 2.3. Дифференциал функции y = ¦(x) dy = y¢(x) dx. Полный дифференциал функции нескольких переменных U = ¦(x, y, z)
где
Правила вычисления дифференциалов
1) d(C u) = C du (C- const), 2) d(u ± v) = du ± dv, 3) d (u v) = u dv +v du, 4) d (u /v) = (v du – u dv) / v2.
Элементы интегрального исчисления Интегрирование– действие обратное дифференцированию ò d¦(x) = ¦(x). Неопределенный интеграл ò ¦(x) dx = Fx + C, где Fx - первообразная функция ( F¢ (x) = ¦ (x)), C - некоторая постоянная. Определенным интегралом от функции y = ¦(x)- называется сумма бесконечно большого числа бесконечно малых слагаемых. b n ¥ ò ¦(x) dx = Lim å ¦ (x i ) Dx I. a Dx 0 i = 1
Геометрический смысл определенного интеграла - это число, равное площади под кривой y = ¦ (x), ограниченной ординатами: a - нижний, b - верхний пределы.
Таблица интегралов
Понятие градиента физической величины Градиент некоторой физической величены U – это вектор, совпадающий с нормалью В декартовой системе
где
Основные физические постоянные
Некоторые астрономические величины
7. Плотности ρ твёрдых тел, жидкостей и газов
8. Диэлектрическая проницаемость ε
9. Удельное сопротивление ρ и температурный коэффициент α проводимости
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. СавельевИ.В. Курс физики/ И.В. Савельев.М.: Наука, 1989. Т.1-3 2. Детлаф А.А. Курс физики/ А.А. Детлаф, Б.М. Яворский. М.: Высш. шк., 1989. 3. Берклеевский курс физики. М.: Наука, 1975-1977.Т. 1-5. 4. Фейман. Лекции по физике/ Фейман. М.: Мир, 1977. Вып. 1-10. 5. Сивухин Д.В. Общий курс физики / Д.В. Сивухин.М: Наука, 1977 1986. Т.1-5. 6. Орир Дж. Физика / Дж. Орир. М.: Мир, 1981. Т.1 –2. 7. Иродов И.Е. Основные законы механики/ И.Е. Иродов. М.: Высш. шк., 1985. 8. Иродов И.Е. Основные законы электромагнетизма / И.Е. Иродов. М.: Высш. шк.,1983. 9. ЯворскийБ.М. Справочник по физике / Б.М. Яворский, А.А. Детлаф. М.: Наука, 1985.
ОГЛАВЛЕНИЕ Введение…………………………………………………………..3 1. МЕХАНИКА..............................................................................8 1.1. Кинематика материальной точки………..………….………....8 1.2. Кинематика поступательного и вращательного движения абсолютно твёрдого тела……...……..….…....12 Примеры решения задач по кинематике………….….....……..15 1.3. Динамика материальной точки и поступательного движения абсолютно твердого тела……….…………....19 1.4. Динамика вращательного движения твердого тела ………………………………………………………22 1.4.1. Момент инерции и момент импульса твердого тела..............................................................................22 1.4.2. Момент силы. Основной закон динамики вращательного движения твердого тела….............25 Примеры решения задач по динамике поступательного и вращательного движения тел………………………................27 1.5. Механическая энергия, работа и мощность…...……..32 1.5.1 Механическая работа и мощность при поступа- тельном движении…………………………………32 1.5.2. Кинетическая и потенциальная энергия……….....34 1.5.3. Работа и мощность при вращательном движении…………………………………………...36 Примеры решения задач на работу и мощность…………........37 1.6. Законы сохранения……………………………………41 1.6.1. Закон сохранения импульса…………..…………42 1.6.2. Закон сохранения момента импульса..…………42 1.6.3. Закон сохранения механической энергии……...43 Примеры решения задач на законы сохранения............……...44 1.7. Механика упругодеформируемых тел…...…...……50 1.7.1 Одноосное растяжение и сжатие…....………….51 1.7.2. Сдвиг…………………………………………….53 Примеры решения задач на деформацию твердых тел…….....56
1.8. Механика жидкостей и газов……………..………..58 1.8.1. Идеальная жидкость. Уравнение неразрыв- ности. Уравнение Бернулли……….……………58 1.8.2. Вязкость. Ламинарный и турбулентный режимы течения жидкостей………………………...……60 Примеры решения задач на механику жидкостей....................62 1.9. Основы релятивистской механики…………….……64 1.9.1. Преобразование координат и принцип относительности Галилея……………………….65 1.9.2. Постулаты специальной теории относительности…………..……………………..67 1.9.3. Преобразования Лоренца. Следствия из преобразований Лоренца………………………..69 1.9.4. Импульс и энергия в релятивистской механике…………………………………….…...73 2. МОЛЕКУЛЯРНАЯ ФИЗИКА……………………………. 76 2.1. Идеальный газ. Уравнение состояния идеального газа……………………………………………………….76 2.2. Основное уравнение молекулярно-кинетической теории…..……………………………………………….78 2.3. Распределение молекул по скоростям ……..………....79 2.4. Барометрическая формула. Распределение Больцмана........................................................................82 2.5. Эффективный диаметр и средняя длина свободного пробега молекул.............................................................83 2.6. Явления переноса…..….………..……………………..84 Примеры решения задач по МКТ…............…………..…….…86 3. ТЕРМОДИНАМИКА……………………………………….. 91 3.1. Внутренняя энергия идеального газа. Равномерное распределение энергии по степеням свободы молекул.……91 3.2. Теплота и работа. Первое начало термодинамики…...….93 3.3. Применение первого начала термодинамики к изопро- цессам. Молярная теплоемкость идеального газа..……..96 3.4. Адиабатный процесс. Уравнение Пуассона..………………97 3.5. Круговые процессы. Цикл Карно. Второе начало термодинамики…………………………………………..99 3.6. Энтропия…..……………………...…………...…………101 Примеры решения задач по термодинамике…..….….………103 4. ЭЛЕКТРОСТАТИКА……...……..………………….112 4.1. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона…………………………………….112 4.2. Электростатическое поле. Напряженность электро- статического поля. Принцип суперпозиции полей…....114 4.3. Линии напряжённости. Поток вектора напряжённости. Теорема Гаусса………………………116 4.4. Работа сил электрического поля. Потенциал………….120 4.5. Эквипотенциальные поверхности. Связь между напряженностью и потенциалом…...…………………123 4.6. Проводники в электрическом поле…….………………125 4.7. Диэлектрики в электрическом поле…..………………..127 4.8. Электроемкость уединенного проводника. Конденсаторы……………………....................................132 4.9. Энергия электрического поля…...………………….....134 Примеры решения задач по электростатике...........................136 5. ЗАКОНЫ ПОСТОЯННОГО ТОКА…………..…………156 5.1. Сила и плотность тока. Сторонние силы, ЭДС и напряжение…..……………………….……………….156 5.2 Обобщённый закон Ома. Дифференциальная форма закона Ома……………………………………………....158 5.3. Работа тока. Закон Джоуля – Ленца…..………………162 5.4. Правила Кирхгофа и их применение к расчёту электрических цепей……………………….…………..164 Примеры решения задач на законы постоянного тока….......166 Задачи для контрольных заданий……………..………...……170 Варианты контрольных заданий….…...….…………………..200 Заключение………………………..…………….………....…..201 Приложения……………………………….…………………….202 Библиографический список…………………………………...210
Учебное издание Москаленко Александр Георгиевич Гаршина Мария Николаевна Сафонов Игорь Александрович Тураева Татьяна Леонидовна
КРАТКИЙ КУРС ФИЗИКИ
Часть 1
МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА. ЭЛЕКТРОДИНАМИКА В авторской редакции
Компьютерный набор И.А. Сафонова
Подписано к изданию 13.10.2011. Объём данных 6,2 МБ.
ФГБОУ ВПО “Воронежский государственный технический университет” 394026 Воронеж, Московский просп., 14
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 496; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.134 (0.009 с.) |

 ,
, - единичные векторы соответствующих координатных осей.
- единичные векторы соответствующих координатных осей.

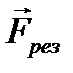
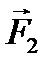
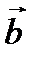

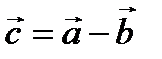

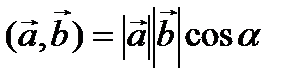 ,
, и
и 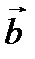 .
.



 и
и  ..
..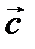 перпендикулярен плоскости в которой располо- жены векторы
перпендикулярен плоскости в которой располо- жены векторы 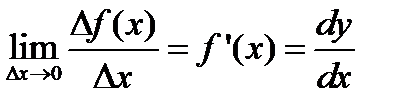
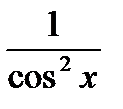
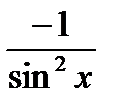
 ,
, - частные производные.
- частные производные.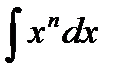
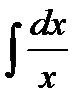



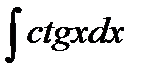







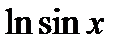
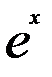

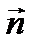 к поверхности одинакового значения U(x,y,z), направленной в сторону его возрастания и имеющий величину ¶ U / ¶ n.
к поверхности одинакового значения U(x,y,z), направленной в сторону его возрастания и имеющий величину ¶ U / ¶ n.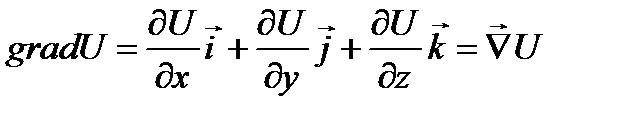 ,
,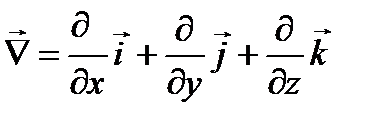 оператор Гамильтона (Набла).
оператор Гамильтона (Набла).


